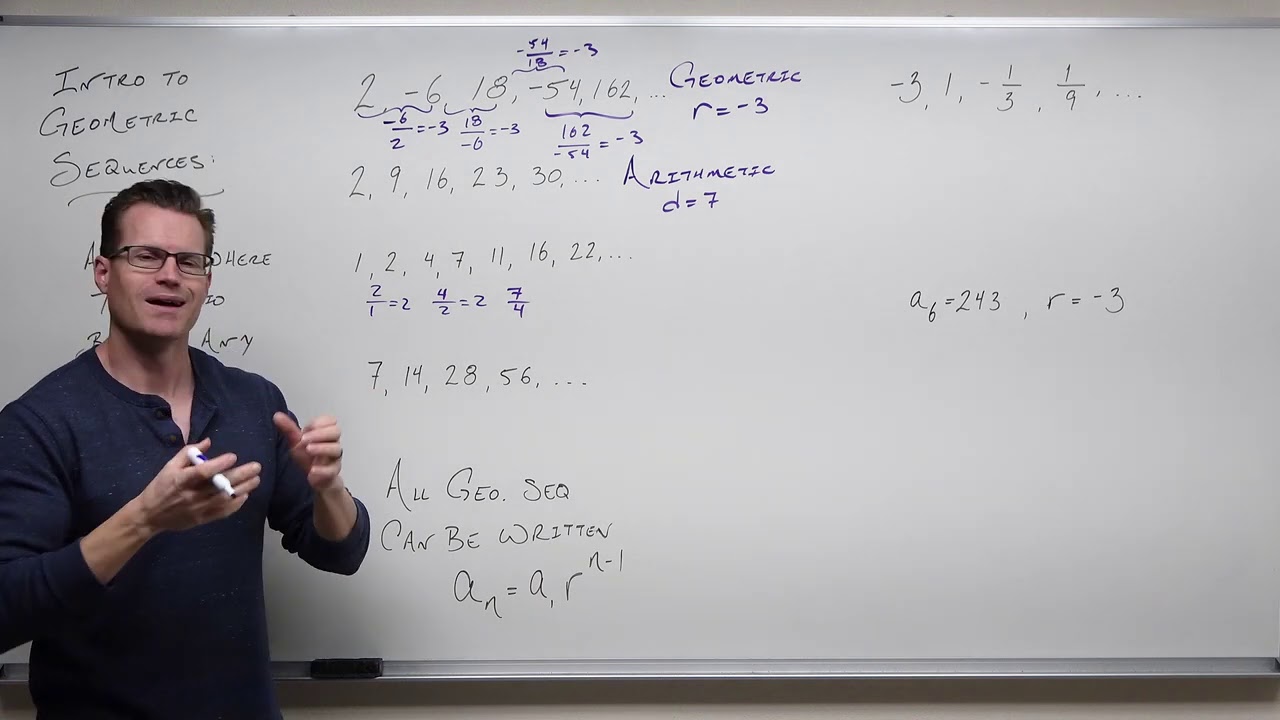Calculus 2 Lecture 9.2: Series, Geometric Series, Harmonic Series, and Divergence Test
TLDRThe video transitions from discussing sequences to exploring series in mathematics. It explains the concept of adding terms of a sequence to form a series, using Sigma notation. The video emphasizes the difference between sequences and series, introduces partial sums, and demonstrates their use in determining the convergence or divergence of a series. It also covers geometric series, harmonic series, and the divergence test, providing examples and shortcuts for identifying and working with these series. The importance of matching exponents and understanding the first term in geometric series is highlighted.
Takeaways
- 📚 The lecture introduces the concept of series, building upon the idea of sequences, focusing on the sum of terms in a sequence rather than just the sequence itself.
- 🔢 Series are represented with Sigma (Σ) notation, which signifies the sum of terms from a starting point to an ending point, often infinity.
- 📈 The concept of partial sums is discussed, which are the sums of the first 'n' terms in a series, and these partial sums create a sequence themselves.
- 🌐 The importance of convergence is highlighted, explaining that if the sequence of partial sums converges, the series converges, and the limit of the partial sums gives the sum of the series.
- 🔍 The lecture demonstrates how to find the sum of a series by finding a formula for the partial sums and then taking the limit as 'n' approaches infinity.
- 📉 It is shown that if the sequence of partial sums diverges, the series also diverges, and it's impossible to find a sum for the series.
- 📝 The process of determining whether a series converges involves finding a partial sum, creating a formula for the partial sums, and then taking the limit as 'n' approaches infinity.
- 📑 The script provides an example of a series with a simple formula for the nth term and demonstrates the steps to determine if the series converges and to find its sum if it does.
- 📚 The concept of a geometric series is introduced, which is a specific type of series where each term is a constant times a common ratio raised to the power of 'n'.
- 📈 The conditions for a geometric series to converge are explained: the common ratio must have an absolute value less than one.
- 📘 A formula for the sum of a convergent geometric series is provided, which is the first term divided by the difference between one and the common ratio.
Q & A
What is the difference between a sequence and a series?
-A sequence is an ordered list of terms, while a series is the sum of the terms of a sequence.
What notation is commonly used to represent a series?
-The Sigma (Σ) notation is commonly used to represent a series, indicating the sum of a sequence of terms.
What is a partial sum in the context of series?
-A partial sum is the sum of the first n terms of a series. It is a finite sum that approximates the series.
How can you determine if a series converges or diverges?
-To determine if a series converges or diverges, you can analyze the sequence of partial sums. If the limit of the partial sums exists and is finite as n approaches infinity, the series converges; otherwise, it diverges.
What is the importance of the limit of a sequence in determining the convergence of a series?
-If the sequence of partial sums converges to a specific number, the series also converges to that number. The limit of the sequence is crucial because it indicates whether the terms are approaching a specific value as n increases.
What is the geometric series formula for the sum of a convergent geometric series?
-The sum of a convergent geometric series can be found using the formula S = a / (1 - r), where a is the first term and r is the common ratio, provided the absolute value of r is less than 1.
When does a geometric series diverge?
-A geometric series diverges if the absolute value of the common ratio r is greater than or equal to 1.
What is the harmonic series, and does it converge or diverge?
-The harmonic series is defined as the sum of the reciprocals of the natural numbers (1 + 1/2 + 1/3 + 1/4 + ...). It diverges.
What is the Divergence Test for series?
-The Divergence Test states that if the limit of the sequence of terms does not equal zero, or does not exist, then the series diverges.
How can you use partial fractions to determine the convergence of a series?
-You can decompose the terms of a series into partial fractions and then analyze the resulting simpler series. If each resulting series is convergent, the original series is convergent. Otherwise, it diverges.
Outlines
📚 Introduction to Series from Sequences
The instructor begins by transitioning from the topic of sequences to series, explaining the concept of series as the sum of terms in a sequence. The focus is on the notation for series, particularly the use of the capital Greek letter Sigma (Σ) to represent the sum. The instructor clarifies the difference between listing terms in a sequence and summing them in a series, emphasizing that series involve adding terms from a starting point to infinity. The concept of partial sums is introduced as a way to consider finite sections of a series, which is essential for understanding convergence and divergence.
🔍 Exploring Partial Sums and Convergence
The instructor delves deeper into the concept of partial sums, which are finite sums of terms in a series up to a certain point. It is explained that for every additional term added to the partial sum, a new sum is created, effectively forming a sequence of partial sums. The importance of this sequence is highlighted in relation to the convergence of the series. If this sequence converges, it implies that the series also converges, and the limit of the partial sums will exist, providing the sum of the series.
🌟 The Relationship Between Sequences and Series
The instructor discusses the relationship between sequences and series, using the example of the sum of the first n terms to illustrate the concept of convergence. The limit of the sequence of partial sums is shown to be equivalent to the series sum when n approaches infinity. The notation and mathematical expressions are explained to help students understand how to determine the convergence of a series and to find its sum if it converges.
📘 Series Convergence and Divergence Criteria
The focus shifts to the criteria for determining the convergence or divergence of a series. The instructor explains that if the sequence of partial sums diverges, the series itself is also divergent. The concept of taking the limit of the partial sum as n approaches infinity is emphasized as a method to determine the series' convergence. Additionally, the instructor provides an example of a simple series and guides students through the process of finding its partial sum and determining its convergence.
📚 Summation of Series and Partial Sums
The instructor provides a detailed explanation of how to find the sum of a series by working with partial sums. The process involves listing the terms of the series, finding a pattern, and then determining the formula for the partial sum. The difficulty of finding this formula is acknowledged, but once it is established, the limit as n approaches infinity can be taken to find the series sum if the sequence of partial sums converges.
📈 Understanding Telescoping Series
The concept of telescoping series is introduced, where many terms in the series cancel each other out, leaving only a few terms that do not cancel. The instructor demonstrates how to identify and work with telescoping series, showing that after cancellation, the remaining terms can be used to find the sum of the series. The process involves recognizing the pattern of cancellation and simplifying the series to its non-cancelling terms.
🔢 Dealing with Complex Series and Partial Fractions
The instructor tackles the topic of complex series and the use of partial fractions to simplify them. The process involves factoring the terms of the series and expressing them as a sum of simpler fractions that may telescope. The example given demonstrates how to break down a complex fraction into a form that can be more easily analyzed for convergence and sum determination.
📖 The Properties of Convergent Series
The instructor discusses the properties of convergent series, explaining that if a series is convergent, the limit of its sequence of terms must equal zero. This is a key concept because it implies that the terms of the series must approach zero for the series to converge. The instructor also mentions that if the limit of the terms does not equal zero, the series must diverge, which is known as the Divergence Test.
📝 Applying the Divergence Test
The Divergence Test is highlighted as a quick method to determine if a series is divergent by taking the limit of its terms. If the limit is not zero, the series is guaranteed to diverge. The instructor emphasizes the importance of this test as a timesaving tool for analyzing series and provides an example to illustrate its application.
🔍 Manipulating Series to Identify Geometric Progression
The instructor guides students through the process of manipulating a given series to identify if it follows a geometric progression. This involves adjusting the exponents to match the index of the series and ensuring that the series fits the form of a geometric series. The example provided demonstrates how to transform a complex series into a recognizable geometric form for easier analysis.
📘 Harmonic Series and Divergence
The instructor introduces the harmonic series, which is the sum of the reciprocals of the natural numbers. Despite the series being composed of positive, decreasing terms, the instructor states that the harmonic series is divergent. This is a key point as it counteracts the common misconception that such a series would converge.
🔗 Subsequences and Series Convergence
The relationship between a sequence and its subsequences in terms of convergence is discussed. The instructor explains that if a sequence converges, any subsequence of it must also converge. Conversely, if a subsequence of a series is divergent, then the entire series must be divergent. This concept is used to prove the divergence of the harmonic series by examining a divergent subsequence.
📌 Convergence and the Limit of Terms
The instructor emphasizes that for a series to converge, the limit of its sequence of terms must be zero. This is a necessary condition for convergence, as the terms of the series must approach zero for the sum to converge. The instructor also clarifies that while a limit of zero is necessary, it is not a sufficient condition on its own for convergence.
📘 Series Manipulation and Convergence Tests
The instructor provides a comprehensive overview of how to manipulate series for easier analysis and how to apply convergence tests. The importance of recognizing geometric series and applying the Divergence Test is highlighted. Additionally, the instructor demonstrates how to break down complex series into simpler components that can be individually tested for convergence.
🔢 Working with Geometric Series and Shortcuts
The instructor discusses the properties of geometric series and provides a shortcut for determining the sum when the powers and indices do not match. The shortcut involves recognizing the first term of the series and using it with the common ratio to find the sum. The instructor also warns against the common mistake of misidentifying the first term and provides clear guidance on how to correctly apply the formula for the sum of a geometric series.
📝 Final Thoughts on Series Analysis
The instructor concludes the lesson with a reminder of the importance of the Divergence Test when analyzing series. They emphasize that checking the limit of the series' terms is a quick and effective way to determine divergence, which can save time on homework and problem-solving. The instructor also encourages students to be meticulous in their approach to avoid common pitfalls when working with series.
Mindmap
Keywords
💡Sequence
💡Series
💡Convergence
💡Divergence
💡Sigma Notation
💡Partial Sum
💡Limit
💡Geometric Series
💡Harmonic Series
💡Divergence Test
Highlights
Introduction to the concept of series, building upon the understanding of sequences.
Explaining the transition from sequences to series by adding terms together.
Introducing Sigma notation for representing sums in series.
Differentiating between sequences and series, emphasizing the addition of terms in series.
Discussing the concept of partial sums and their role in understanding series.
Describing the process of finding the sum of a series by examining partial sums.
The importance of recognizing when a series is finite and when it is infinite.
Teaching how to determine if a series converges or diverges using limits and partial sums.
The relationship between the convergence of a sequence of partial sums and the convergence of a series.
Using the limit of partial sums to find the sum of a convergent series.
The significance of the limit in determining the sum of an infinite series.
Providing a step-by-step approach to finding the sum of a series, including finding a formula for partial sums.
Illustrating the process with a simple example series and calculating its partial sums.
Demonstrating the concept of telescoping series and how they simplify the process of finding the sum.
The method of partial fractions as a tool for simplifying complex series.
Identifying and proving the formula for geometric series and their convergence criteria.
Teaching the formula for the sum of a geometric series and when it can be applied.
Using the Divergence test to quickly determine if a series is divergent.
Properties of convergent series, such as factoring out constants and splitting series into the sum of two series.
Highlighting the importance of checking the convergence of each part of a series when dealing with multiple series.
Providing a shortcut for dealing with geometric series when powers do not match the index.
Concluding with advice on using the Divergence test for series and emphasizing the importance of understanding the first term in a series.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: