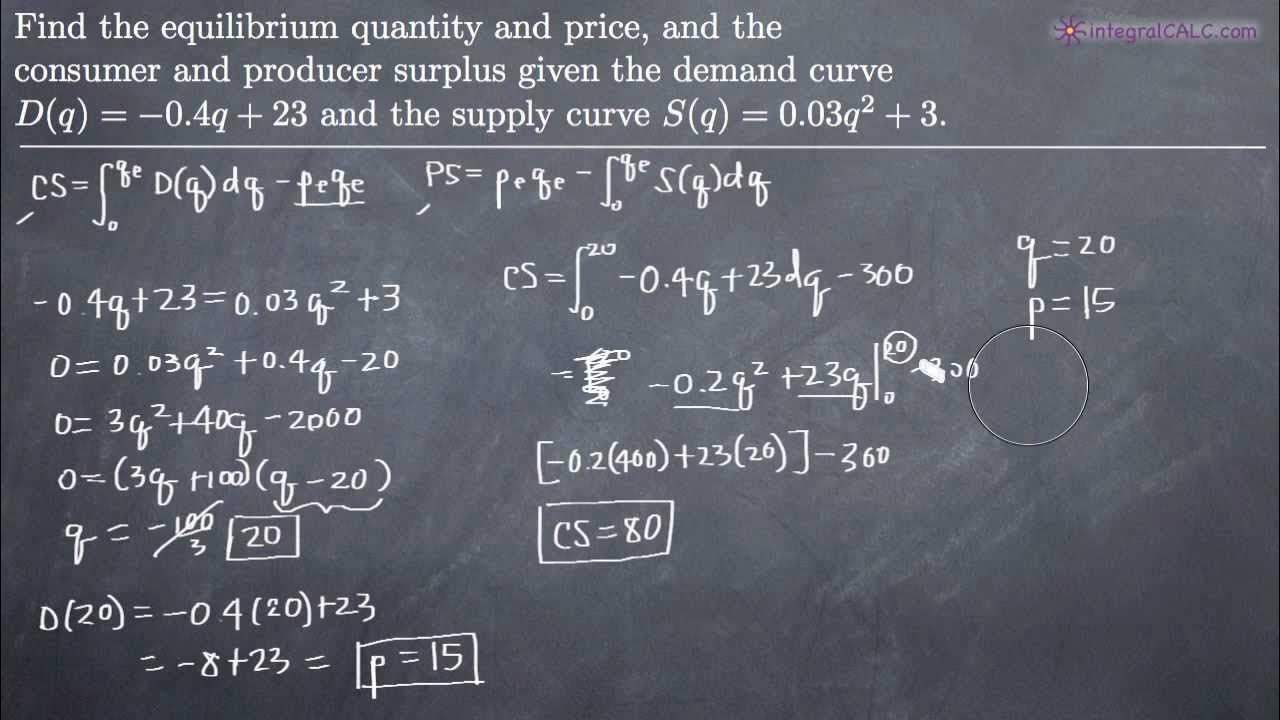Business Calculus: Producer and Consumer Surplus

Rajendra Dahal
4 Nov 202105:51
EducationalLearning
32 Likes 10 Comments

TLDRThe video script explains the calculation of consumer surplus (CS) and producer surplus (PS) in an economic context. It uses a given demand function and a supply function to find the equilibrium point at a price of 60 dollars and a quantity of 10 units (in hundreds). The CS is computed by integrating the demand function from 0 to 10 and subtracting the area under the price line, resulting in a CS of 13,333.33. Similarly, the PS is found by integrating the supply function and subtracting the total cost from the total revenue at equilibrium, yielding a PS of 116,666.66. The explanation highlights the process of integrating and evaluating functions to find economic surpluses.

Takeaways
  • 📈 The problem involves finding the consumer surplus (CS) and producer surplus (PS) given a demand function and a supply function.
  • 📊 The demand function D(x) is represented as -0.2x^2 + 80, where p is the unit price in dollars and x is the quantity demanded in units of a hundred.
  • 📉 The supply function S(x) is provided and the equilibrium point is given as (10, 60), where x is the quantity and p is the price.
  • 🔍 The equilibrium point notation used is x̄ for quantity and p̄ for price.
  • 🧮 To find the consumer surplus, the formula used is the integral from 0 to x̄ of the demand function minus p̄ * x̄.
  • 🔢 The integration of the demand function from 0 to 10 is performed and evaluated to find the consumer surplus.
  • 📉 The final consumer surplus value is calculated to be 13,333.33 dollars after adjusting for the unit measure in hundreds.
  • 💵 The producer surplus is calculated using the formula p̄ * x̄ minus the integral of the supply function from 0 to x̄.
  • 📐 The integration of the supply function from 0 to 10 is performed and evaluated to find the producer surplus.
  • 🔍 The final producer surplus value is calculated to be 11,666.67 dollars after adjusting for the unit measure in hundreds.
Q & A

  • What is the formula for calculating consumer surplus (CS)?

    -The consumer surplus (CS) is calculated by integrating the demand function from 0 to the equilibrium quantity (x̄) and then subtracting the total expenditure at the equilibrium price (p̄x̄). In the script, it is given as the integral from 0 to x̄ of the demand function (10 - 0.2x²) dx, minus p̄x̄.

  • What is the formula for calculating producer surplus (PS)?

    -Producer surplus (PS) is calculated by subtracting the integral of the supply function from 0 to the equilibrium quantity (x̄) from the total revenue at the equilibrium price (p̄x̄). In the script, it is given as p̄x̄ minus the integral from 0 to x̄ of the supply function (0.1x² + x + 40) dx.

  • What is the demand function in terms of x and p?

    -The demand function is given as d = 10 - 0.2x², where p is the unit price in dollars and x is the quantity demanded in units of a hundred.

  • What is the supply function given in the script?

    -The supply function is given as s = 0.1x² + x + 40, which represents the quantity supplied in the market as a function of the price.

  • What is the equilibrium point mentioned in the script?

    -The equilibrium point is given as (x̄, p̄) = (10, 60), which means the market reaches equilibrium when the quantity demanded equals the quantity supplied at a price of 60 dollars for 100 units of the product.

  • How is the consumer surplus calculated in the script?

    -The consumer surplus is calculated by integrating the demand function from 0 to 10, which is 10 - 0.2x², and then subtracting 600 (6 times 10 times the equilibrium price of 60). The result is then adjusted for the units of hundred, yielding a consumer surplus of 133,333.33 in dollars.

  • What is the process for calculating the producer surplus as described in the script?

    -The producer surplus is calculated by integrating the supply function from 0 to 10, which is 0.1x² + x + 40, and then subtracting this result from 600 (the equilibrium price times the equilibrium quantity). The final result is then adjusted for the units of hundred.

  • What is the final calculated value for consumer surplus in the script?

    -The final calculated value for consumer surplus is 133,333.33 dollars, after adjusting for the units of hundred.

  • What is the final calculated value for producer surplus in the script?

    -The final calculated value for producer surplus is approximately 116,666.67 dollars, after adjusting for the units of hundred.

  • Why is it necessary to adjust the final answers for the units of hundred?

    -The adjustment is necessary because the demand and supply functions are given in terms of x being the quantity demanded or supplied in units of a hundred, so the final surplus values need to reflect the actual monetary value.

  • What does the script imply about the relationship between consumer and producer surplus at the equilibrium point?

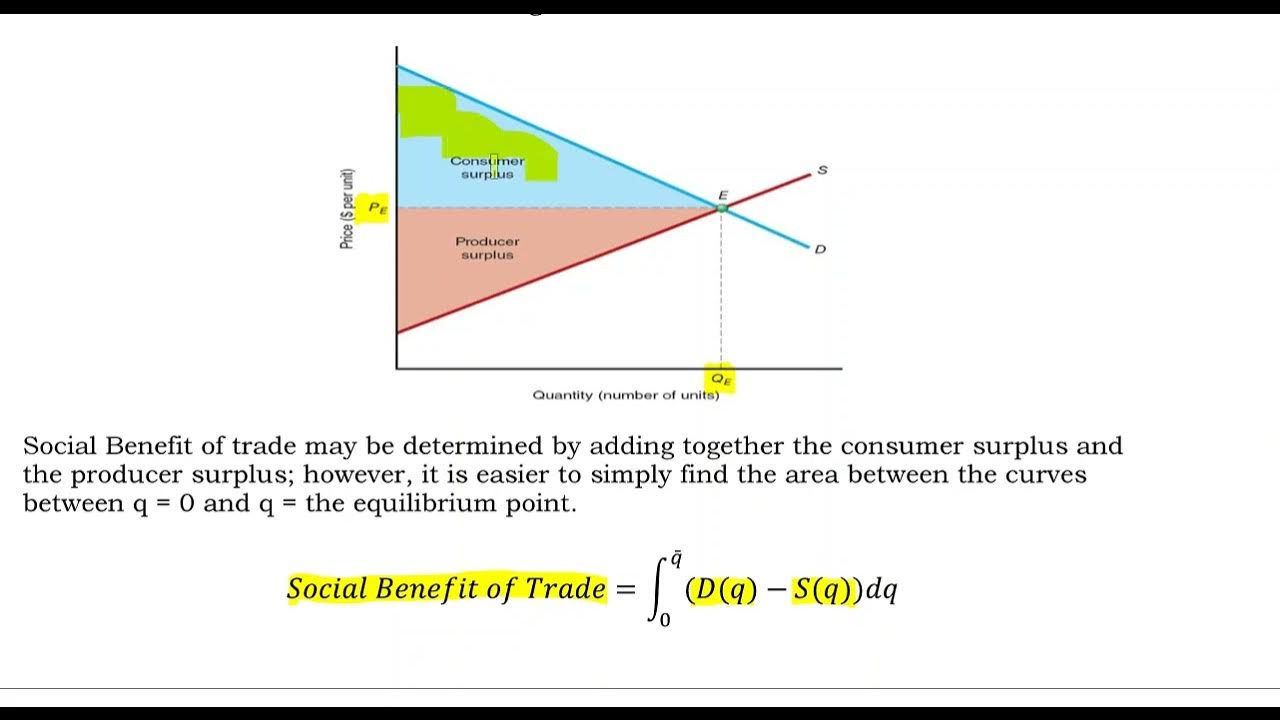
    -The script implies that at the equilibrium point, the sum of consumer and producer surplus represents the total welfare gained from the market transaction, which is the difference between what consumers are willing to pay and what they actually pay, and what producers are willing to accept and what they actually receive.

Outlines
00:00
📚 Calculating Consumer Surplus

The first paragraph of the script focuses on the calculation of consumer surplus (CS) in an economic context. It introduces the formula for CS and explains the process of finding the equilibrium point where the quantity demanded meets the quantity supplied. The demand function is given in terms of 'x', which represents the quantity demanded in units of a hundred. The script then proceeds to integrate the demand function from 0 to the equilibrium quantity 'x bar', subtracting the total area under the price line at 'p bar'. The final step is to convert the result into the correct units by multiplying by 100, yielding the consumer surplus amount.

05:01
💼 Determining Producer Surplus

The second paragraph continues the economic analysis by calculating the producer surplus (PS). It starts with the equilibrium quantity 'x bar' and the price 'p bar', then integrates the supply function from 0 to 'x bar'. The supply function is given in terms of 'x', and the integration process involves calculating the area under the supply curve up to the equilibrium point. The total revenue, represented by 'p bar' times 'x bar', is then subtracted from the integrated supply function to find the producer surplus. The result is adjusted for the units by multiplying by 100, providing the final figure for the producer surplus in dollars.

Mindmap
Keywords
💡Consumer Surplus
Consumer surplus is the difference between what consumers are willing to pay for a good or service and what they actually pay. It is a measure of the perceived benefit or economic welfare gained by consumers. In the video, the script calculates consumer surplus using the demand function and the equilibrium point, which is a central part of understanding market efficiency and consumer benefit.
💡Producer Surplus
Producer surplus is the difference between the minimum price that producers are willing to accept for a good or service and the actual price they receive. It represents the profit or economic welfare gained by producers. The video script describes the calculation of producer surplus using the supply function and the equilibrium quantity, which is crucial for assessing the profitability and market performance of producers.
💡Demand Function
A demand function is a mathematical relationship that shows the quantity of a good or service that consumers are willing to purchase at various prices. In the script, the demand function is given in terms of 'x' and 'p', where 'x' is the quantity demanded in units of a hundred, and 'p' is the unit price in dollars, illustrating how consumer demand varies with price.
💡Supply Function
A supply function is a mathematical relationship that shows the quantity of a good or service that producers are willing to supply at various prices. The script mentions the supply function, which is essential for understanding how the quantity supplied changes with price and is used to calculate producer surplus.
💡Equilibrium Point
The equilibrium point in economics is where the quantity demanded by consumers equals the quantity supplied by producers, resulting in a stable market price and quantity. The script identifies the equilibrium point as '(x bar, p bar)', which is used to calculate both consumer and producer surplus.
💡Integration
Integration is a fundamental concept in calculus that represents the process of finding the area under a curve between two points. In the video, integration is used to calculate the areas representing consumer and producer surplus, which is essential for understanding the total economic welfare in the market.
💡Anti-Derivative
An anti-derivative is a function that reverses the process of differentiation. In the context of the video, anti-derivatives are used to find the integral of the demand and supply functions, which is necessary for calculating the areas under the curves that represent consumer and producer surplus.
💡Economic Welfare
Economic welfare refers to the overall economic well-being of individuals or groups within an economy. The video script discusses consumer and producer surplus as measures of economic welfare, highlighting the importance of these concepts in assessing the benefits derived from market transactions.
💡Market Efficiency
Market efficiency is a state where resources are allocated in a way that maximizes the total welfare of consumers and producers. The script's discussion of consumer and producer surplus is directly related to market efficiency, as these surpluses indicate how well the market is meeting the needs and desires of both parties.
💡Units of a Hundred
In the script, the quantity demanded 'x' is measured in units of a hundred, which is a common practice for simplifying calculations and making the data more manageable. This unit conversion is important when interpreting the final results of the consumer and producer surplus calculations.
💡Calculus
Calculus is a branch of mathematics that deals with rates of change and accumulation. The video script uses calculus, specifically integration, to solve for consumer and producer surplus, demonstrating the practical application of this mathematical tool in economic analysis.
Highlights

Introduction to the task of finding consumer surplus (CS) and producer surplus (PS) using given formulas.

Explanation of the demand function d in terms of x, where p is unit price and x is quantity demanded in units of a hundred.

Clarification that x is given in hundreds, not as a direct quantity.

Introduction of the supply function that determines how much the company is willing to supply.

Identification of the equilibrium point as (1060), with x representing the independent variable.

Notation of equilibrium point as (x-bar, p-bar).

Calculation of consumer surplus using the integral of the demand function from 0 to x-bar and subtracting p-bar times x-bar.

Integration of the demand function terms: -0.2x^2 and 80.

Antiderivatives found for the demand function: x^3/3 for -0.2x^2 and 80x for the constant term.

Evaluation of the integral from 0 to 10 and subtraction of 600 (6 times 10 times p-bar).

Calculation result for consumer surplus: 1333.33, adjusted for units of a hundred.

Introduction to the calculation of producer surplus using the supply function integrated from 0 to x-bar.

Integration of the supply function terms: 0.1x^2, x, and 40.

Antiderivatives found for the supply function: x^3/3 for 0.1x^2, x^2/2 for x, and 40x for the constant term.

Evaluation of the integral and subtraction from 600 to find the producer surplus.

Calculation result for producer surplus: 11616, adjusted for units of a hundred.

Final consumer surplus rounded to 1333.33 and producer surplus rounded to 1166.67.

Transcripts

Browse More Related Video

Consumer and Producer Surplus (KristaKingMath)

Consumer Surplus (CS) and Producer Surplus (PS) Example

Consumers' Surplus Producers' Surplus from given Demand and Supply functions

consumers' surplus Example

Social Benefit of Trade (Gains from Trade)

consumer surplus and producer surplus

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
EconomicsConsumer SurplusProducer SurplusDemand FunctionSupply FunctionEquilibrium AnalysisMathematical IntegrationMarket EquilibriumEconomic TheoryQuantitative AnalysisPrice Determination