Perfect Substitutes Utility: Compensating Variation, Equivalent Variation, and Consumer Surplus

Economics in Many Lessons
21 Jul 202105:35
EducationalLearning
32 Likes 10 Comments

TLDRThis video tutorial explores the concept of consumer welfare using a perfect substitutes utility function. The scenario involves a consumer with a $12 income, facing a price increase for good x from $1 to $1.50. The video demonstrates how to calculate compensating variation, equivalent variation, and the change in consumer surplus. It concludes with the consumer's optimal choice to purchase only good x before and after the price increase, highlighting the impact of price changes on consumer behavior and welfare.

Takeaways
  • 📚 The video is about using a perfect substitutes utility function to calculate three measures of consumer welfare.
  • 💰 The consumer has an income of twelve dollars and faces different prices for goods X and Y, which form the budget constraint.
  • 🔍 The utility function is used to determine the marginal utility per dollar for goods X and Y, which helps decide the optimal consumption choice.
  • 🛒 The consumer opts to buy only good X before and after the price increase due to its higher marginal utility per dollar.
  • 📈 The compensating variation is calculated to find out how much additional income is needed to maintain the same utility level after a price increase.
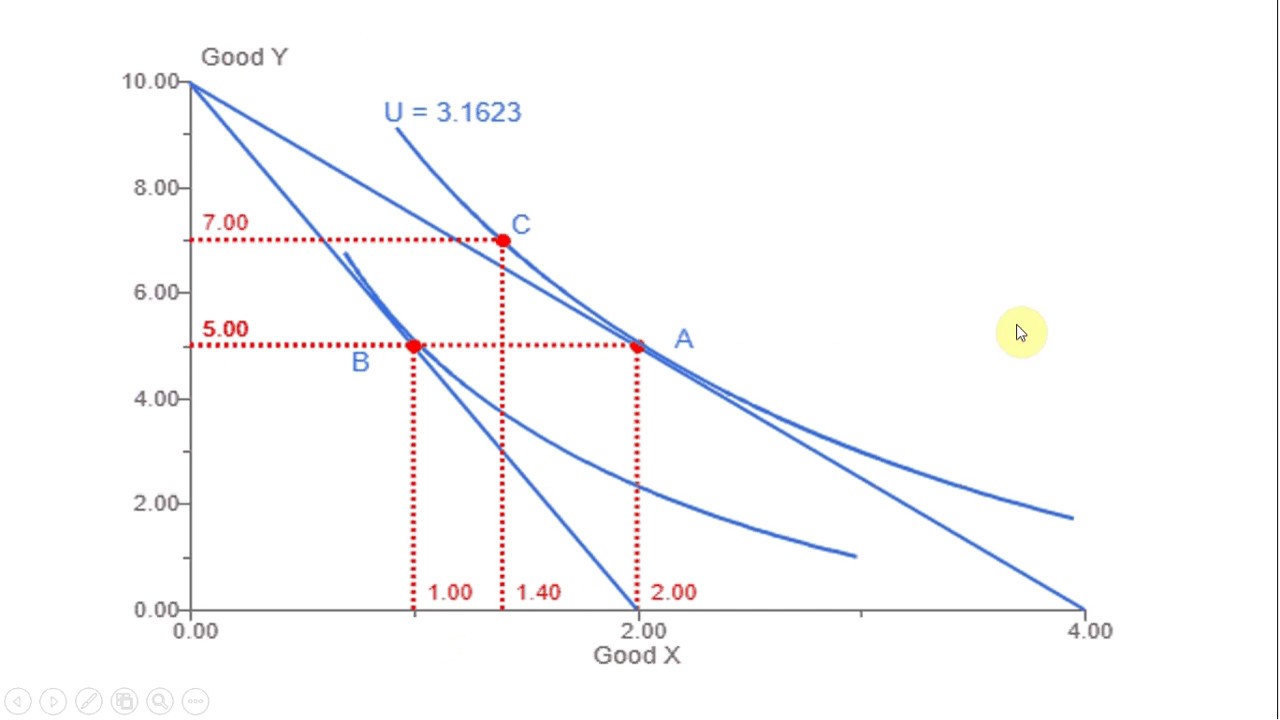
  • 💡 The compensating variation is found to be six dollars, which offsets the price increase of good X from one dollar to one dollar and fifty cents.
  • 📉 The equivalent variation measures the amount the consumer would be willing to pay to avoid the price increase, and it is calculated to be four dollars.
  • 🧮 The change in consumer surplus is determined by integrating the demand for good X over the price change, resulting in a loss of four dollars and 87 cents.
  • 📊 The video demonstrates the use of calculus to solve for the integral and evaluate the change in consumer surplus.
  • 📚 The script concludes with a summary of the three measures of consumer welfare calculated in the video.
Q & A

  • What is the utility function used in the video?

    -The utility function used in the video is a perfect substitutes utility function, where the consumer has a preference for one good over another based on the marginal utility per dollar spent.

  • What is the consumer's income in the scenario presented in the video?

    -The consumer's income in the scenario is twelve dollars.

  • What are the initial prices of goods X and Y in the video?

    -The initial price of good X is one dollar, and the price of good Y is two dollars.

  • How does the consumer determine which good to buy before the price increase?

    -The consumer determines which good to buy by comparing the marginal utility per dollar for each good. In this case, good X has a higher marginal utility per dollar, so the consumer chooses to buy good X.

  • What is the concept of compensating variation?

    -Compensating variation is the amount of money that would need to be given to a consumer to completely offset a price increase, so that the consumer's utility remains unchanged, staying on the same indifference curve.

  • How much is the price of good X increased to in the video?

    -The price of good X is increased from one dollar to one dollar and fifty cents.

  • What is the new budget constraint after the price increase of good X?

    -After the price increase of good X to one dollar and fifty cents, the new budget constraint is such that the consumer can only afford to buy eight units of good X with their twelve dollars of income.

  • What is the concept of equivalent variation?

    -Equivalent variation is the amount of money a consumer would be willing to give up in order to not face a price increase, maintaining the same level of utility as before the price change.

  • What is the amount of compensating variation calculated in the video?

    -The compensating variation calculated in the video is six dollars, which is the difference between the new income needed to maintain the same utility level after the price increase and the original income.

  • What is the amount of equivalent variation calculated in the video?

    -The equivalent variation calculated in the video is four dollars, which represents the amount the consumer would be willing to give up to avoid the price increase.

  • How is the change in consumer surplus calculated in the video?

    -The change in consumer surplus is calculated by integrating the demand function for good X from the original price to the new price and evaluating the integral, which in this case results in a loss of four dollars and 87 cents of consumer surplus.

Outlines
00:00
📚 Calculating Consumer Welfare with Utility Functions

This paragraph introduces a video on economic concepts, focusing on the use of a perfect substitutes utility function to measure consumer welfare. It explains the consumer's income, the prices of two goods (X and Y), and the budget constraint equation. The goal is to calculate compensating variation, equivalent variation, and change in consumer surplus due to a price increase of good X. The video uses the marginal utility per dollar approach to determine the optimal consumption choice, concluding that the consumer will only buy good X before and after the price increase, as it provides more utility per dollar spent.

05:00
📈 Consumer Surplus Impact of Price Increase

The second paragraph delves into the calculation of the compensating variation, which is the amount needed to offset the price increase and maintain the consumer's original utility level. It details the process of finding the new budget constraint after the price increase and determining the compensating variation as a monetary value. The paragraph also explains the equivalent variation, which is the amount the consumer would willingly sacrifice due to the price increase, and how it is calculated using the original and new budget constraints. Finally, the video addresses the change in consumer surplus, using calculus to integrate the demand function and determine the loss in consumer surplus due to the price increase of good X.

Mindmap
Keywords
💡Perfect Substitutes Utility Function
A perfect substitutes utility function is a specific type of utility function where consumers are indifferent between consuming more of one good and less of another, as long as the overall utility remains the same. In the context of the video, it is used to determine the optimal consumption choice for a consumer with a given income and prices for two goods, X and Y. The function helps in calculating measures of consumer welfare, such as compensating variation and equivalent variation.
💡Consumer Welfare
Consumer welfare refers to the economic concept that measures the economic well-being of consumers, often in terms of the satisfaction they derive from consumption. In the video, three measures of consumer welfare are calculated: compensating variation, equivalent variation, and change in consumer surplus. These measures help to understand the impact of a price change on a consumer's utility.
💡Compensating Variation
Compensating variation is an economic measure that represents the amount of money that would need to be given to a consumer to keep them at the same level of utility after a price change. In the video, it is calculated by determining the income level that would provide the same utility as the original scenario with the new, higher price of good X.
💡Equivalent Variation
Equivalent variation is another economic measure that indicates the amount of money a consumer would be willing to give up to avoid a price increase, thus maintaining the same level of utility. In the video, it is calculated by finding the income level that would provide the same utility as the scenario with the new price and the original income.
💡Consumer Surplus
Consumer surplus is the difference between what consumers are willing to pay for a good and what they actually pay. It is a measure of the perceived benefit of a good to the consumer. In the video, the change in consumer surplus is calculated after a price increase for good X, indicating the loss in consumer benefit.
💡Marginal Utility
Marginal utility is the additional satisfaction a consumer gets from consuming one more unit of a good. In the video, the marginal utility per dollar for good X and good Y is compared to determine which good provides more utility for the consumer's money, guiding the consumer's purchasing decision.
💡Budget Constraint
A budget constraint is the limit on consumption set by a consumer's income and the prices of goods. In the video, the budget constraint is used to determine the maximum quantity of goods X and Y the consumer can buy with their income, which is crucial for calculating compensating and equivalent variations.
💡Price Increase
A price increase refers to a rise in the cost of a good or service. In the video, the price of good X increases from $1 to $1.50, which affects the consumer's purchasing power and leads to the calculation of compensating and equivalent variations to measure the impact on consumer welfare.
💡Income
Income is the total monetary compensation received by an individual or household over a period of time. In the video, the consumer's income is $12, which is used in conjunction with the prices of goods X and Y to determine the consumer's optimal consumption choice and the effects of a price change.
💡Indifference Curve
An indifference curve on a graph represents all the combinations of two goods that provide the consumer with the same level of satisfaction or utility. In the video, the concept of staying on the same indifference curve is used to explain the purpose of calculating compensating variation, which is to maintain the consumer's utility level despite a price change.
Highlights

Introduction to using the perfect substitutes utility function to calculate consumer welfare measures.

Consumer has an income of twelve dollars with goods priced at one dollar for good x and two dollars for good y.

Formation of the budget constraint equation: income equals price of good x times units of good x plus price of good y times units of good y.

Calculation of compensating variation, equivalent variation, and change in consumer surplus due to a price increase of good x.

Determination of which good provides the most marginal utility per dollar, favoring good x over good y.

Consumer's decision to buy only good x before and after the price increase, as it remains the more efficient choice.

Calculation of compensating variation as six dollars to offset the price increase and maintain the same utility level.

Explanation of compensating variation as the difference in income needed to achieve the same utility with the new price.

Introduction to equivalent variation, the amount a consumer would give up to avoid the price increase.

Calculation of equivalent variation as four dollars based on the new utility level with the higher price of good x.

Analysis of the original and new budget constraints to determine the change in consumer's purchasing power.

Calculation of consumer surplus change using integral calculus to find the area between the demand curve and the new price.

Determination of the change in consumer surplus as negative four dollars and 87 cents due to the price increase.

Summary of the three measures of consumer welfare: compensating variation, equivalent variation, and change in consumer surplus.

Conclusion emphasizing the usefulness of the video in understanding the impact of price changes on consumer welfare.

Transcripts

Browse More Related Video

Three Measures of Consumer Welfare: Compensating Variation, Equivalent Variation, Consumer Surplus

16. Compensating Variation and Equivalent Variation

Consumer Welfare: Compensating Variation & Equivalent Variation

How to Calculate Compensating Variation and Equivalent Variation

Mathematically Solving for the Income and Substitution Effect of a Price Change

(M4E8) [Microeconomics] Consumer Surplus: Compensating and Equivalence Variations

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Consumer WelfareUtility FunctionPrice IncreaseCompensating VariationEquivalent VariationConsumer SurplusEconomic AnalysisDemand CurveIncome EffectSubstitute GoodsEconomic Theory