Infinite Series

RH Mathematics

24 Feb 202222:59

EducationalLearning

32 Likes 10 Comments

TLDRThis video script delves into the concept of infinite series in calculus, starting with the basics of sequences and moving on to series definitions and notation. It explains the divergence test for series, highlighting examples of divergent and possibly convergent series. The script introduces geometric series, their tests for convergence, and the formula for their sums. It also touches on power series, discussing their convergence based on the common ratio. The video aims to prepare viewers for deeper explorations into series in subsequent lessons.

Takeaways

📚 The video introduces the concept of infinite series and sequences, with an assumption of no prior knowledge from the viewers.
🔢 A sequence is defined as an ordered list of numbers or a function that takes in whole numbers.
📈 The script explains series using the sigma notation, emphasizing the sum of terms from n=1 to n=p.
🌐 The focus of the video is on infinite series, which extend to infinity, and the importance of the first step in analyzing a series by writing out its terms.
📊 The divergence test is highlighted as a method to determine if a series diverges by checking if the limit of its terms is not zero.
❌ The video provides examples of series that diverge using the divergence test, such as series with terms growing faster than their denominators.
✅ It mentions that a series may possibly converge if the limit of its terms is zero, as demonstrated with the natural log of n divided by n squared plus 1.
🍰 An analogy of eating a cake over several days illustrates how a series can converge to a total, showing the concept of partial sums and convergence.
📉 The harmonic series is introduced as an example of a series that diverges even though its terms approach zero.
🔄 The geometric series is discussed, with emphasis on the common ratio and the condition for convergence being the absolute value of the ratio being less than one.
🔢 The formula for the sum of a convergent geometric series is presented, along with a strategy to avoid fraction arithmetic errors.

Q & A

What is the main topic of discussion in this video?
-The main topic of discussion in this video is infinite series, which will be explored in depth over the next two units in calculus BC.
What is a sequence in the context of this video?
-A sequence, in this context, is an ordered list of numbers that can also be represented as a function taking in whole numbers only, such as the sequence 10, 20, 30, 40, 50, 60, and so on.
What is the large sigma operator used for in the script?
-The large sigma operator is used to denote the sum of a series, indicating that you are adding together a sequence of terms.
What is the difference between a series and a sequence according to the video?
-A sequence is an ordered list of numbers or a function with whole number inputs, while a series is the sum of the terms in a sequence, as indicated by the large sigma operator.
What is the divergence test mentioned in the video?
-The divergence test is a theorem stating that if the limit of the terms of a series is not zero, then the series definitely diverges, meaning it does not converge to a finite value.
Why is the series sum from n=1 to infinity of 2n an example of divergence according to the video?
-The series sum from n=1 to infinity of 2n is an example of divergence because as n gets larger, the terms 2n keep increasing without bound, indicating the series cannot converge to a finite value.
What is the harmonic series and why does the video mention it diverges?
-The harmonic series is the series sum from n=1 to infinity of 1/n. The video mentions it diverges because, despite the terms getting smaller, they do not approach zero quickly enough to ensure convergence.
What is a geometric series and how is it defined in the video?
-A geometric series is a series where each term is a constant multiple, known as the common ratio, of the previous term. In the video, examples given include 1/2^n and 1.05^n.
What is the condition for a geometric series to converge according to the video?
-According to the video, a geometric series converges if and only if the absolute value of the common ratio is less than one.
What is a power series and how does it relate to the discussion in the video?
-A power series is an infinite series that includes variables, often considered as an infinite degree polynomial. The video introduces the concept and discusses the conditions under which it converges.
How does the video explain the convergence of the series sum from n=0 to infinity of (x+1)^n / 3^n?
-The video explains that this series is a geometric series with a common ratio of (x+1)/3. It converges if the absolute value of this ratio is less than one, which is determined by solving the inequality |(x+1)/3| < 1.

Outlines

00:00

📚 Introduction to Infinite Series in Calculus

The video begins with an introduction to infinite series, a topic that will be explored extensively in the upcoming calculus units. The instructor clarifies that no prior knowledge of series is assumed, as some precalculus classes cover them while others do not. The concept of sequences as ordered lists of numbers is introduced, with the sequence being a function that takes only whole numbers. The instructor emphasizes that while sequences are important, the focus is on what is contained within a series. The anatomy of a series is explained using the sigma notation, including the index, starting point, and terms being summed. The video sets the stage for a deep dive into series, including the investigation of infinite series that extend to infinity.

05:01

🔍 The Divergence Test and Series Examples

This paragraph delves into the divergence test, a theorem stating that if the limit of the terms of a series does not approach zero, the series must diverge. The instructor provides examples of series and applies the divergence test to determine if they converge or diverge. The series involving powers of 2 and 1.05 are shown to diverge due to their terms growing without bound. However, the series with terms of 5n/(10n+3) is identified as diverging because its terms approach a non-zero limit. The instructor also mentions a series involving the natural log of n, which suggests potential convergence due to the terms approaching zero. The concept of convergence is introduced, with the partial sums of a series being used to determine if the series converges to a finite value.

10:01

🎂 The Concept of Convergence with a Cake Analogy

Using a birthday cake analogy, the instructor illustrates the concept of convergence. The scenario involves eating half of the cake each day, with the amount eaten represented as a series. The instructor shows that as days go by, the total amount eaten approaches the whole cake, demonstrating convergence. The series of 1/2^n is used as an example, with the instructor explaining that the partial sums approach one, indicating convergence to that value. The importance of understanding convergence in calculus is highlighted, especially in the context of series that do not have a simple formula for their sum.

15:02

📉 Harmonic Series and Geometric Series Divergence

The instructor introduces the harmonic series, which is a series of the reciprocals of natural numbers, and states that it diverges despite its terms approaching zero. This serves to emphasize that terms approaching zero is necessary but not sufficient for convergence. The concept of geometric series is then explored, with examples provided and the divergence of certain geometric series explained using the divergence test. The instructor also discusses the geometric series test, which determines convergence based on the common ratio's absolute value being less than one. The formula for the sum of a convergent geometric series is introduced, and an example from a past calculus exam is used to demonstrate its application.

20:04

🔢 Power Series and Their Convergence Criteria

The final paragraph introduces power series, which are series involving variables and can be thought of as infinite-degree polynomials. The instructor explains how to identify the convergence of a power series by writing out its terms and determining the common ratio. An example is given where the series involves an offset index, and the instructor demonstrates how to find the interval of x values for which the series converges by solving an inequality involving the common ratio. The importance of understanding the convergence of power series is highlighted, setting the stage for further exploration in future lessons.

Mindmap

Keywords

💡Infinite Series

An infinite series is the sum of the terms in a sequence that continues indefinitely. In the context of the video, the theme revolves around understanding and analyzing such series in calculus. The script discusses infinite series as a central concept, using examples like the sum of '2n' from n=1 to infinity, to illustrate the concept of divergence.

💡Divergence Test

The divergence test is a method used to determine whether an infinite series diverges. It states that if the limit of the series' terms as n approaches infinity is not zero, the series must diverge. The script uses the divergence test to analyze series like 2^n/n^3, concluding that it diverges because the terms do not approach zero.

💡Convergence

Convergence in the context of series refers to the property of an infinite series where the sum of its terms approaches a finite value. The video explains that if the limit of the partial sums exists, the series is said to converge. The script provides the example of the series 1/2^n, showing that it converges to 1.

💡Sequence

A sequence is an ordered list of numbers, and it can also be thought of as a function that takes in whole numbers. In the video, sequences are introduced as the building blocks of series, with the script using the example of a simple counting sequence like 10, 20, 30, etc., to explain the concept.

💡Sigma Notation

Sigma notation is a symbol used in mathematics to represent the sum of a sequence of terms. The script introduces the large sigma symbol to denote the summation in a series, such as in the series ∑ from n=1 to ∞ of 2n, where it signifies the addition of all terms of the form 2n for n starting from 1 to infinity.

💡Geometric Series

A geometric series is a type of series where each term is a constant multiple, known as the common ratio, of the previous term. The video discusses geometric series as a special case of series that can be easily analyzed for convergence. Examples from the script include (1/2)^n and 1.05^n, explaining their behavior based on the common ratio.

💡Harmonic Series

The harmonic series is a specific type of series where the terms are the reciprocals of the natural numbers, such as 1/1 + 1/2 + 1/3 + ... The script mentions the harmonic series as an example of a series that diverges, despite its terms approaching zero.

💡Power Series

A power series is an infinite series where the terms are powers of a variable, often x. The video introduces power series as a significant topic in calculus, discussing their convergence and the importance of understanding their behavior. The script uses an example of a power series with terms involving (x+1)/3^n to illustrate the concept.

💡Common Ratio

The common ratio in a geometric series is the factor by which each term is multiplied to get the next term. The video explains that the convergence of a geometric series is determined by the absolute value of the common ratio being less than one. The script uses the series 3/2 * (3/8)^n to demonstrate finding the common ratio and applying the convergence criteria.

💡Partial Sums

Partial sums refer to the sum of the first k terms of an infinite series. The script explains that the definition of convergence for an infinite series is related to the limit of its partial sums. The example of eating a cake over several days is used to illustrate the concept of partial sums and how they approach the total amount of the cake eaten.

Highlights

Introduction to infinite series in calculus BC, assuming no prior experience with series.

Sequences defined as ordered lists of numbers and functions taking whole numbers.

Explanation of the anatomy of a series with the large sigma operator.

Series defined as the sum of terms with an index and formula.

Focus on infinite series in AP Calculus and their investigation.

Use of the divergence test to determine if a series diverges.

Demonstration of the divergence test with examples.

Explanation of the geometric series and its properties.

Geometric series test to ascertain convergence based on the common ratio.

Formula for the sum of a convergent geometric series.

Example from the 1997 BC exam to find the value a series converges to.

Introduction to power series and their significance in calculus.

Analysis of a power series with an offset index.

Determination of values of x for which a power series converges.

Explanation of how to handle series with different powers of n.

The importance of practicing problem-solving with series.

Encouragement to return for further learning about series.

Transcripts

Browse More Related Video

Calculus BC Unit 11 Recap

Calculus 2 Lecture 9.6: Absolute Convergence, Ratio Test and Root Test For Series

Comparison Tests | MIT 18.01SC Single Variable Calculus, Fall 2010

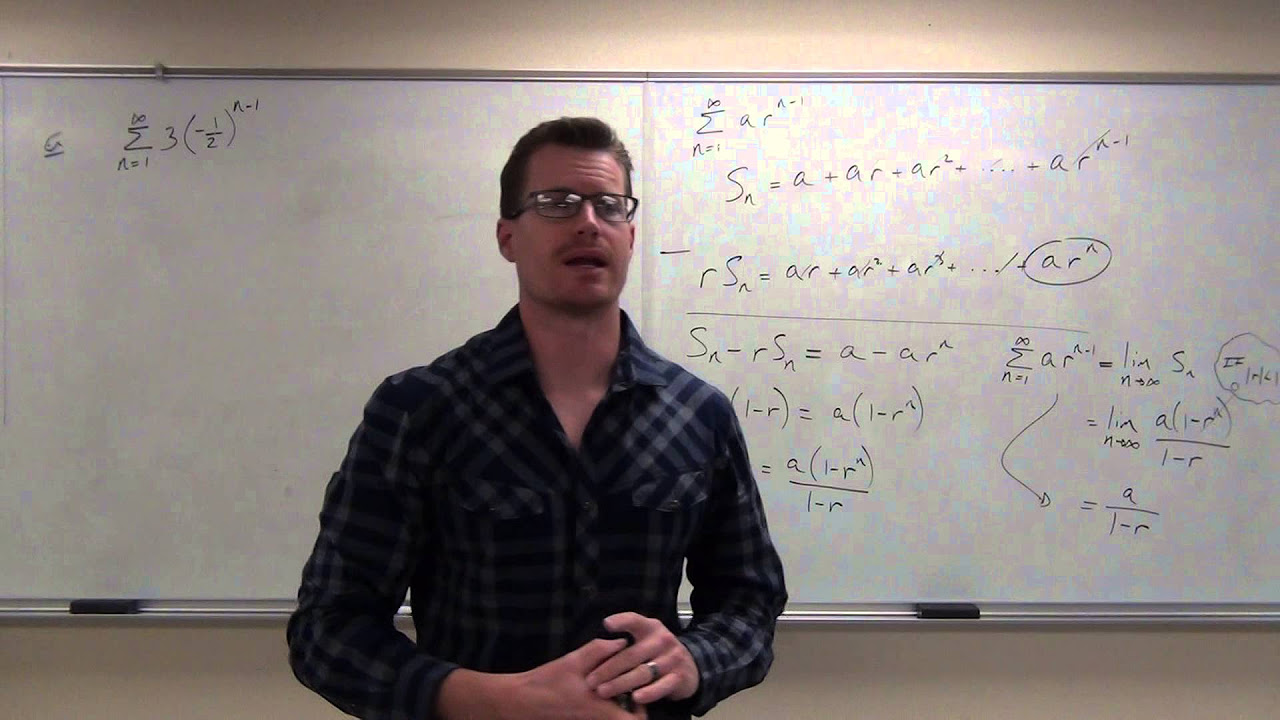
Calculus 2 Lecture 9.2: Series, Geometric Series, Harmonic Series, and Divergence Test

Tests for Convergence

Unit 10 Study Guide - AP Calculus (BC Only)

Related Tags

Infinite Series Calculus BC Sequences Divergent Test Convergence Geometric Series Harmonic Series Power Series Math Education Series Convergence