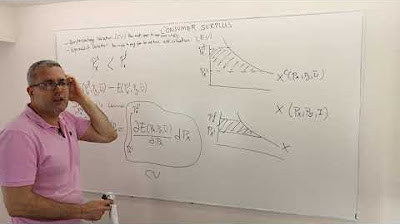
Three Measures of Consumer Welfare: Compensating Variation, Equivalent Variation, Consumer Surplus
TLDRThis educational video explores three measures of consumer welfare in response to price changes, using a quasi-linear utility function as an example. It explains consumer surplus, compensating variation, and equivalent variation, illustrating how each measure evaluates the impact of price changes on consumer well-being. The video demonstrates calculations for these measures with a specific price increase scenario, revealing a consistent two-dollar welfare loss across all methods for a normal good, and emphasizes the simplicity of estimating consumer surplus despite its limitations.
Takeaways
- 📈 The video discusses three measures of consumer welfare in response to a price change: consumer surplus, compensating variation, and equivalent variation.
- 💰 Consumer surplus is calculated as the dollar difference between what a consumer is willing to pay and what they actually spend, but it doesn't hold utility constant.
- 🔄 Compensating variation measures the amount of money needed to compensate a consumer for a price increase so that it's not harmful, considering utility is held constant.
- 🔄 Equivalent variation measures how much money a consumer would be willing to give up to avoid a price increase, also holding utility constant.
- 📚 The script uses a quasi-linear utility function to illustrate the calculation of these measures, considering a consumer with a fixed income.
- 🛒 The example involves a price increase of good X from $1 to $2, with the original budget constraint and utility maximization under the new prices.
- 📉 The compensating variation is calculated by determining the income difference needed to maintain the same utility level after the price increase.
- 📈 The equivalent variation is found by calculating the income difference needed to achieve the same utility level at the original utility function with the new prices.
- 📊 For a normal good, the welfare effect of a price change is such that compensating variation exceeds the change in consumer surplus, which in turn exceeds the change in equivalent variation.
- 🔄 For a quasi-linear utility function, all three measures give the same welfare effect for a good with no income effect.
- 📉 For an inferior good, the inequality signs for the welfare effects would be flipped.
- 🔎 For small price changes, all three measures of consumer welfare are similar, suggesting that uncompensated demands might be easier to estimate despite their limitations.
Q & A
What are the three measures of consumer welfare discussed in the video?
-The three measures of consumer welfare discussed are consumer surplus, compensating variation, and equivalent variation.
What is the main issue with using consumer surplus to measure the effect of a price change on consumer welfare?
-Consumer surplus does not hold utility constant when analyzing the effect of a price change, as it includes both substitution and income effects.
How is compensating variation defined in the context of this video?
-Compensating variation is the amount of money a consumer needs to be compensated so that a price increase does not harm them, holding utility constant.
What is the process to calculate compensating variation?
-To calculate compensating variation, first maximize utility at the original prices, then find the income level necessary with the new prices to achieve the same utility, and the difference in income levels is the compensating variation.
What is equivalent variation and how is it calculated?
-Equivalent variation is the amount of money a consumer would be willing to give up to avoid a price increase, holding utility constant. It is calculated by maximizing utility at the new prices with the original income and then finding the income level necessary with the original prices to achieve the same utility.
How does the welfare effect of a price change differ for a normal good and an inferior good?
-For a normal good, compensating variation exceeds the change in consumer surplus, which exceeds the change in equivalent variation. For an inferior good, these inequality signs are flipped.
What is a quasi-linear utility function and why is it used in this video?
-A quasi-linear utility function is a type of utility function where the utility of one good is additively separable from income. It is used in this video to simplify the analysis of consumer welfare measures without income effects.
What is the consumer's original income and the prices of goods x and y in the example provided?
-The consumer's original income is ten dollars, with the original price of good x being one dollar and the price of good y being two dollars.
What is the new price of good x after the increase, and how does this affect the calculation of compensating variation?
-The new price of good x is two dollars. This increase affects the calculation of compensating variation by requiring a new income level to achieve the same utility as before the price increase.
How much is the compensating variation in the example with a price increase of good x from one to two dollars?
-The compensating variation in the example is two dollars, which is the difference between the new required income of twelve dollars and the original income of ten dollars.
What is the change in consumer surplus when the price of good x increases from one to two dollars?
-The change in consumer surplus is a loss of two dollars due to the price increase of good x from one to two dollars.
Outlines
📊 Introduction to Consumer Welfare Measures
This paragraph introduces the concept of consumer welfare and its measurement through three different methods in the context of a price change. The focus is on using a quasi-linear utility function to analyze the impact of price changes on consumer welfare. The methods discussed include consumer surplus, compensating variation, and equivalent variation. Consumer surplus is the difference between what consumers are willing to pay and what they actually pay. Compensating variation measures the amount of money needed to offset the negative utility impact of a price increase, while equivalent variation measures the amount of money a consumer would forgo to avoid a price increase. The paragraph also touches upon the challenges of estimating these measures and the implications of different types of goods on welfare calculations.
🔍 Calculating Compensating Variation
The second paragraph delves into the calculation of compensating variation using a specific utility function and given prices and income. It describes a scenario where the price of good x increases from one to two dollars, and the consumer has an initial income of ten dollars. The process involves maximizing utility at the original prices to determine the consumer's optimal consumption levels, then recalculating at the new prices to find the income level that would yield the same utility. The compensating variation is the difference between the original and new income levels required to maintain the same utility, which in this case is two dollars, indicating a two-dollar welfare loss due to the price increase.
📉 Equivalent Variation and Change in Consumer Surplus
The final paragraph discusses the calculation of equivalent variation and the change in consumer surplus. Equivalent variation is determined by finding the income level at the original prices that would provide the same utility as the new price scenario, resulting in a two-dollar difference, consistent with the compensating variation. The change in consumer surplus is calculated by integrating the demand curve, reflecting a two-dollar decrease due to the price increase of good x. The paragraph concludes that all three measures of consumer welfare indicate a two-dollar welfare loss, reinforcing the consistency of these measures for small price changes.
Mindmap
Keywords
💡Consumer Welfare
💡Quasi-Linear Utility Function
💡Consumer Surplus
💡Compensating Variation
💡Equivalent Variation
💡Price Change
💡Income Effect
💡Substitution Effect
💡Ordinary Demand
💡Budget Constraint
💡Marginal Utility
Highlights
Introduction to three measures of consumer welfare in response to a price change using a quasi-linear utility function.
Explanation of consumer surplus as the dollar difference between the maximum willingness to pay and actual market expenditure.
Limitations of consumer surplus in holding utility constant during price change analysis.
Introduction to compensating variation as a measure that holds utility constant post-price change.
Methodology for calculating compensating variation through utility maximization at original and new prices.
Explanation of equivalent variation as another measure of welfare that considers the amount a consumer would forgo due to a price increase.
Step-by-step calculation of equivalent variation using utility maximization at new and original prices.
The relationship between compensating variation, change in consumer surplus, and equivalent variation for normal goods.
Special case of a quasi-linear utility function where all three welfare measures yield the same value for a good with no income effect.
Inversion of the welfare effect inequality for inferior goods.
Argument for the practicality of consumer surplus despite its limitations due to easier estimation.
Detailed walkthrough of calculating compensating variation with a given utility function and price change.
Demonstration of maximizing utility under a new price scenario to find compensating variation.
Calculation of equivalent variation by determining the income level that replicates original utility at new prices.
Analysis of the change in consumer surplus through integral calculus following a price increase.
Conclusion that all three measures indicate a two-dollar welfare loss due to the price increase.
Final summary emphasizing the similarity of the three measures for small price changes and the ease of estimating uncompensated demands.
Transcripts
Browse More Related Video

Perfect Substitutes Utility: Compensating Variation, Equivalent Variation, and Consumer Surplus

16. Compensating Variation and Equivalent Variation

Consumer Welfare: Compensating Variation & Equivalent Variation
(M4E8) [Microeconomics] Consumer Surplus: Compensating and Equivalence Variations
Calculating the area of Deadweight Loss (welfare loss) in a Linear Demand and Supply model

How to Calculate Compensating Variation and Equivalent Variation
5.0 / 5 (0 votes)
Thanks for rating: