AP Calculus BC Lesson 10.1
TLDRThis transcript introduces sequences and series in AP Calculus BC, explaining the difference between finite and infinite sequences and how to represent them with explicit formulas. It delves into the concept of series as the sum of sequence terms, using summation notation, and discusses the convergence and divergence of infinite series. The role of partial sums in determining the convergence of a series is highlighted, with examples illustrating the process of finding terms, partial sums, and the series sum. The importance of understanding the relationship between a sequence's partial sums and its convergence properties is emphasized, providing a foundation for further study in calculus.
Takeaways
- 📚 Introduction to sequences and series, distinguishing between finite and infinite sequences.
- 🔢 Explanation of explicit formulas for sequences, such as a_n = 2n + 2, and how to find specific terms using the formula.
- 📈 Understanding the concept of partial sums (S_n) and how they relate to the convergence of a series.
- 🌐 Divergent series example: the series from n=1 to Infinity of 2n + 2, which increases without bound.
- 🌐 Convergent series example: the series from n=1 to Infinity of 1/(3^n), which approaches 1 as n approaches Infinity.
- 🔑 The relationship between the limit of partial sums (S_n) and the convergence or divergence of an infinite series.
- 📊 Process of determining if a sequence converges or diverges by examining its pattern and partial sums.
- 📈 Example of divergent series: the series from n=1 to Infinity of 5n^2, which grows without bound.
- 🔢 Explanation of how to find the nth term of a sequence given an explicit formula, such as a_n = (-1)^n + 2.
- 📊 Method for calculating the sum of the first n terms of a series and the sum of an infinite series using limits.
- 🔍 Identification of the correct nth partial sum that converges to a given value by analyzing the limit as n approaches Infinity.
Q & A
What is the difference between a finite sequence and an infinite sequence?
-A finite sequence is an ordered list of terms with a limited number of elements, such as 4, 6, 8, 10. An infinite sequence, on the other hand, continues indefinitely, often represented with a formula and ellipsis, like 4, 6, 8, 10, ... to indicate the ongoing pattern.
How is the nth term of a sequence denoted?
-The nth term of a sequence is denoted as a_sub_n, where 'n' represents the position of the term in the sequence. For instance, a_sub_1 would be the first term, a_sub_2 the second term, and so on.
What is the explicit formula for the sequence 4, 6, 8, 10, ...?
-The explicit formula for the given sequence is a_sub_n = 2n + 2, where 'n' is the position of the term in the sequence.
What is a series in the context of mathematics?
-A series is the sum of the terms in a sequence. It can be finite or infinite, and is often represented using summation notation, such as the sum from n=1 to n=4 of 2n + 2.
How do you find the sum of the first n terms of a sequence?
-The sum of the first n terms of a sequence, also known as the partial sum, is denoted as S_sub_n. It is found by adding the terms a_1, a_2, ..., a_n together.
What happens to the series when the sequence of partial sums diverges?
-If the sequence of partial sums S_sub_n diverges, meaning it increases without bound or does not approach a specific value, then the infinite series also diverges. It does not converge to a specific sum but instead approaches positive or negative infinity.
What is the relationship between the sum of an infinite series and the limit of its sequence of partial sums?
-The sum of an infinite series from n=1 to infinity of a_sub_n is equal to the limit as n approaches infinity of the sequence of partial sums S_sub_n. This means the series converges to the value that the sequence of partial sums approaches as more terms are added.
How can you determine if the series 1/(2^n) converges or diverges?
-The series 1/(2^n) converges because the terms of the sequence decrease and approach zero as n increases. The sequence of partial sums approaches a limit, which can be found to be 1, indicating that the series converges to this value.
What is the pattern observed in the sequence given by a_sub_n = (-1)^n + 2?
-The sequence oscillates between 1 and 3, depending on whether n is odd or even. For odd values of n, a_sub_n is 1, and for even values, it is 3.
What is the sum of the infinite series from n=1 to infinity of (-3/n)?
-The sum of this infinite series is not directly given, but by examining the first few terms and the pattern, we can infer that the series diverges since the terms do not approach a limit as n increases.
Given the nth partial sum S_sub_n = (2^n) / (3n + 8) for an infinite series, what is the sum of the series?
-The sum of the series is found by taking the limit as n approaches infinity of the nth partial sum S_sub_n, which in this case is (2/3) as the terms 2^n and 3n in the denominator cancel out, leaving 2/3.
What expression defines the sequence 1, 3, 1, 9, 1, 27, 1, 81...?
-The expression for the sequence is a_sub_n = 1 / (3^n), where 'n' is the position of the term in the sequence, and this pattern is observed as the sequence follows the powers of 3.
Outlines
🔢 Introduction to Sequences and Series
This paragraph introduces the foundational concepts of sequences and series within the context of AP Calculus BC. It distinguishes between finite and infinite sequences, using a simple numeric sequence as an example to illustrate the concept of an explicit formula, which defines the nth term of a sequence. The role of 'n' as the position indicator within a sequence is clarified, and the paragraph transitions into the concept of series, defined as the sum of sequence terms, demonstrated through summation notation. The distinction between finite and infinite series is made, setting the stage for deeper exploration of infinite series and concepts like divergence, partial sums, and their relevance in understanding the behavior of series over infinite terms.
📊 Working with Sequences and Series
The second paragraph delves into practical examples of calculating terms in a sequence and sums of series. It starts with a specific sequence formula and asks for the first five terms and the sum of the first four terms, S Sub 4, demonstrating the process of plugging in values to find specific terms. The narrative continues with another example sequence, emphasizing the difference between finding a specific term in a sequence (a sub 3) and the sum of terms up to a certain point (S Sub 3). The paragraph underscores the importance of understanding series as the sum of sequence terms and introduces the concept of partial sums and their convergence or divergence, laying the groundwork for understanding how sequences and series behave over infinite terms.
🔄 Convergence and Divergence in Series
This paragraph examines the concepts of convergence and divergence in series, starting with an example series to illustrate how a sequence's terms and their partial sums can indicate whether a series converges to a value or diverges. The explanation includes a detailed analysis of the sequence and its partial sums, leading to the conclusion that the series converges to 1. The narrative progresses to more examples, demonstrating through term analysis and partial sums whether each series converges or diverges, emphasizing the practical application of these concepts in determining the behavior of series over infinite terms.
🧐 Analyzing Sequence Patterns and Series Behavior
The fourth paragraph focuses on analyzing specific sequences and the behavior of their corresponding series. It starts with a sequence where the terms oscillate between two values, concluding that the sequence diverges due to its lack of convergence to a single value. The narrative then transitions to a series example, guiding through the process of finding the first five terms of the sequence's partial sums to conclude about the series' convergence or divergence. This segment reinforces the difference between sequence and series analysis and the importance of partial sums in understanding series behavior.
📈 Advanced Series Analysis Techniques
The fifth paragraph introduces more advanced techniques for analyzing series, starting with an example where the nth partial sum is given, and the task is to find the series' sum. The explanation includes taking the limit of the nth partial sum as n approaches infinity, illustrating a method to determine a series' convergence to a specific value. Several examples follow, each presenting a different scenario of series and their nth partial sums, and demonstrating how to use limits to conclude the series' behavior, highlighting the diversity of approaches in series analysis.
Mindmap
Keywords
💡Sequence
💡Series
💡Explicit Formula
💡Partial Sums
💡Convergence
💡Divergence
💡Limit
💡nth Term
💡Summation Notation
💡Diagonal Asymptote
Highlights
Introduction to sequences and series in AP Calculus BC.
Definition of finite and infinite sequences with examples.
Explanation of explicit formulas for sequences and how to use them.
How to find specific terms in a sequence using the explicit formula.
Definition and calculation of a series as the sum of terms in a sequence.
Use of summation notation in representing series.
Explanation of partial sums and their role in series.
How the limit of partial sums determines the convergence or divergence of an infinite series.
Example of a series that diverges and the concept of divergence.
Method to find the first five terms of a sequence given an explicit formula.
Procedure to calculate the sum of a series using the limit of partial sums.
Explanation of the convergence of the series 1/(2^n) and its sum.
Analysis of a series with a given formula for the nth partial sum and determination of the series sum.
Guidelines for identifying the correct nth partial sum that converges to a given value.
Method to derive the explicit formula for a sequence from a given list of terms.
Discussion on the convergence or divergence of a sequence and its relation to series convergence.
Transcripts
Browse More Related Video
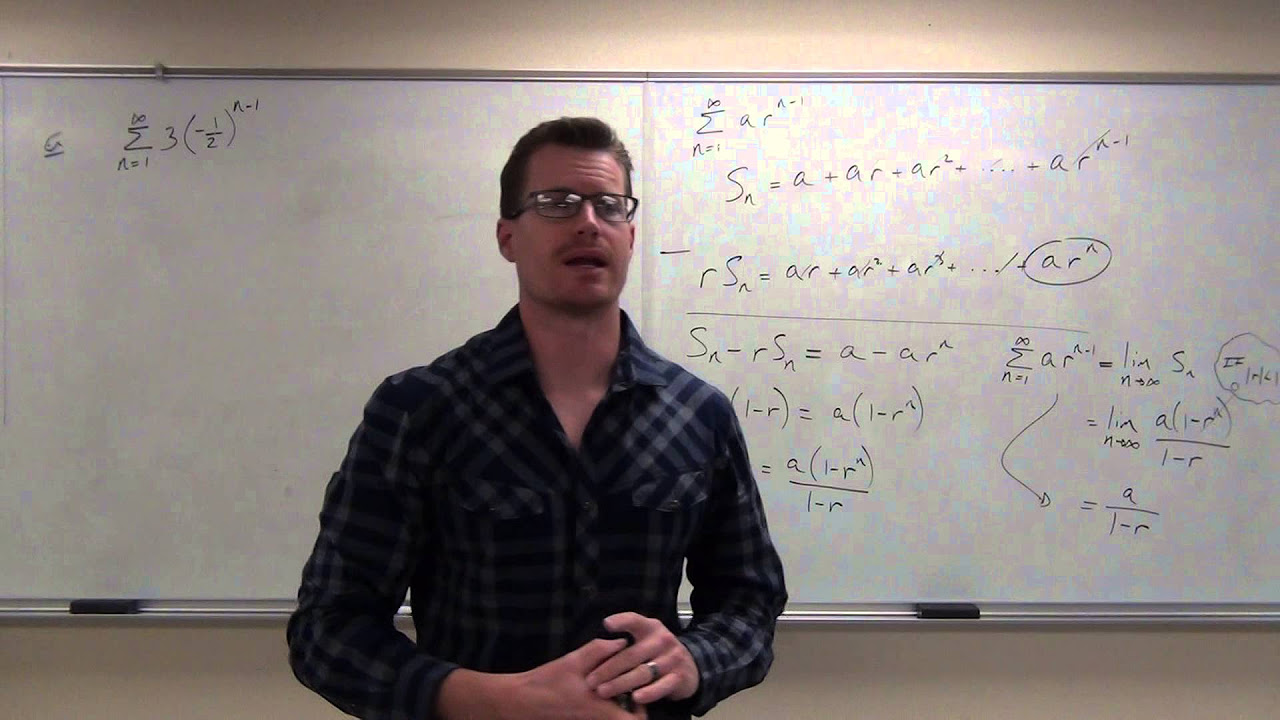
Calculus 2 Lecture 9.2: Series, Geometric Series, Harmonic Series, and Divergence Test

Unit VII: Lec 1 | MIT Calculus Revisited: Single Variable Calculus

Ch. 12.1 Sequences and Summation Notation

Calculus BC – 10.10 Alternating Series Error Bound

Lesson 18 - Integral Test (Calculus 2 Tutor)

Partial sums intro | Series | AP Calculus BC | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: