What are Degrees of Freedom?

3than_224
3 Jun 201506:14
EducationalLearning
32 Likes 10 Comments

TLDRThe video script delves into the concept of 'degrees of freedom' (DF), a term frequently encountered in statistics and psychology. Initially challenging to grasp, the presenter aims to clarify its meaning through an example involving a distribution of numbers, illustrating how deviations from a mean must sum to zero. The script explains that degrees of freedom represent the number of values in a system that can independently vary, often calculated as one less than the total number of values (n-1). This concept is crucial for understanding statistical calculations and the presenter hopes to help viewers build a better grasp of the underlying principles.

Takeaways
  • 📚 Degrees of freedom is a term often used in statistics, first encountered by the speaker in an introductory psychology class.
  • 🤔 The concept of degrees of freedom can be challenging to understand, as it was for the speaker's professor and classmates.
  • 📝 The degrees of freedom is denoted by the symbol DF and is crucial for various statistical calculations.
  • 🧩 Understanding degrees of freedom can help in reconstructing formulas and solving statistical problems.
  • 🔢 Degrees of freedom refers to the number of values within a system that are free to vary.
  • 📈 The speaker uses an example of a distribution of numbers (like the number of apples people have) to illustrate degrees of freedom.
  • 🍎 In the example, the mean number of apples is calculated, and deviations from the mean are determined for each person.
  • ⚖️ Deviations from the mean in a system must sum up to zero, which is a key rule in understanding variability.
  • 🔗 Knowing two of the three deviations, the third is restricted and not free to vary, which is central to the concept of degrees of freedom.
  • 📉 The degrees of freedom for a system of three numbers is two, as only two numbers can be freely assigned before the third is determined.
  • 📐 The general formula for degrees of freedom is n minus 1, where n is the total number of values in a set or distribution.
Q & A

  • What is the term 'degrees of freedom' often used in?

    -The term 'degrees of freedom' is most often used in statistics classes.

  • Why is understanding the concept of degrees of freedom important?

    -Understanding the concept of degrees of freedom is important because it is used in many different statistical calculations and can help in remembering and applying formulas.

  • What is the symbol used for degrees of freedom?

    -The symbol used for degrees of freedom is DF, sometimes with dots in between them.

  • What does the term 'degrees of freedom' represent in a statistical context?

    -In a statistical context, 'degrees of freedom' represents the number of values within a system that are free to vary.

  • Can you provide an example to illustrate the concept of degrees of freedom?

    -An example given in the script is a distribution of three numbers (e.g., number of apples people have). The mean is calculated, and deviations from the mean are determined. The degrees of freedom for this system is two because the third value is determined by the requirement that the deviations sum to zero.

  • Why do the deviations in a system have to sum up to zero?

    -The deviations in a system have to sum up to zero because it is a rule when discussing variability in statistics.

  • How is the last value in a system of deviations determined?

    -The last value in a system of deviations is determined by the requirement that the total sum of deviations equals zero.

  • What is the general formula for calculating degrees of freedom in a set of numbers?

    -The general formula for calculating degrees of freedom is DF = n - 1, where n is the number of values or terms within a distribution or set of numbers.

  • How does the concept of degrees of freedom relate to the idea of a system of numbers?

    -The concept of degrees of freedom relates to a system of numbers by determining how many of those numbers can vary independently while still maintaining the constraints of the system, such as the sum of deviations being zero.

  • What is the significance of degrees of freedom in statistical analysis?

    -The significance of degrees of freedom in statistical analysis is that it helps in understanding the variability within a dataset and is crucial for many statistical tests and calculations.

Outlines
00:00
📚 Understanding Degrees of Freedom in Statistics

The first paragraph of the video script introduces the concept of degrees of freedom (DF), a term frequently encountered in statistics. The speaker reminisces about their initial struggle to grasp the term during an introductory psychology and statistics class. The script highlights the importance of understanding degrees of freedom beyond just calculating it, as it plays a crucial role in various statistical calculations. The speaker suggests that understanding the concept can help in reconstructing formulas when forgotten. An example is used to illustrate degrees of freedom, explaining it as the number of values in a system that can vary freely. The example involves a distribution of three numbers, such as the number of apples people have, and how these numbers deviate from the mean. It's explained that since deviations must sum up to zero, the last value in the system is not free to vary, thus reducing the degrees of freedom by one. This example aims to clarify the abstract definition of degrees of freedom, which is the amount of values that are unrestricted in a system.

05:02
📐 General Equation for Degrees of Freedom

The second paragraph delves into the general equation for calculating degrees of freedom. It simplifies the concept by stating that degrees of freedom is typically calculated as the total number of values (n) minus one (n - 1). The speaker emphasizes that this formula is applicable in various statistical distributions or sets of numbers. The rationale is that once all but one of the values in a distribution are determined, the last value is inherently restricted by the requirement that the sum of the distribution equals a certain value. This restriction means that only one less than the total number of values can vary freely, hence the formula n - 1. The paragraph concludes by reinforcing the explanation provided in the first paragraph and thanks the viewers for their attention.

Mindmap
Keywords
💡Degrees of Freedom (DF)
Degrees of Freedom (DF) is a fundamental concept in statistics that refers to the number of values within a system that are free to vary. In the context of the video, it is used to explain how certain statistical calculations are made, particularly those involving the variance of a dataset. The script uses the example of a distribution of numbers (e.g., the number of apples people have) to illustrate how deviations from the mean sum up to zero, thereby limiting the last value's freedom to vary, which is why the degrees of freedom for a system of three numbers is two (n-1, where n is the total number of values).
💡Statistics
Statistics is a branch of mathematics that deals with the collection, analysis, interpretation, presentation, and organization of data. In the video, the concept of degrees of freedom is introduced as a term often encountered in statistics classes, specifically in an introductory psychology course. It is a key component in various statistical calculations, which is why understanding it is essential for students and practitioners in the field.
💡Variance
Variance is a measure of the dispersion or spread of a set of data points. It is calculated as the average of the squared differences from the mean. In the script, variance is mentioned in the context of calculating how much each person deviates from the mean number of apples. Understanding variance is crucial for assessing the degree of variation within a dataset, which is directly related to the concept of degrees of freedom.
💡Mean
The mean, often referred to as the average, is a measure of central tendency in a set of numbers. It is calculated by summing all the values and then dividing by the number of values. In the video, the mean is used to find the average number of apples among three groups of people. The mean is essential for calculating deviations, which in turn are used to determine the degrees of freedom.
💡Deviation
Deviation refers to the difference between an individual data point and the mean of a dataset. In the script, deviations are calculated to find out how much each person's number of apples deviates from the mean. These deviations are crucial for understanding the concept of degrees of freedom because they must sum to zero, which restricts the last value in the system.
💡Psychology
Psychology is the scientific study of the human mind and its functions, particularly those affecting behavior. The video mentions that the concept of degrees of freedom was first encountered in an introductory psychology class. This indicates that statistical concepts like degrees of freedom are relevant in understanding and analyzing psychological data.
💡Formula
A formula in mathematics or statistics is a concise way of expressing information symbolically as relations between quantities. The script mentions the formula for degrees of freedom, which is n-1, where n is the total number of values in a dataset. Understanding formulas is essential for performing statistical calculations and for grasping the underlying principles of statistical concepts.
💡Distribution
A distribution in statistics refers to the way data points are spread across a range of values. The script uses the example of a distribution of numbers to explain the concept of degrees of freedom. The distribution is a key element in understanding how the values are spread and how the degrees of freedom are determined based on the constraints of the system.
💡System
In the context of the video, a system refers to a set of values or data points that are being analyzed. The script uses the term to describe a set of numbers, such as the number of apples people have, and how these numbers interact with each other to determine the degrees of freedom. The system is a fundamental concept in understanding how statistical calculations are made.
💡Education
Education is the process of acquiring knowledge, skills, values, and habits. The video script discusses the challenges of learning the concept of degrees of freedom in an educational setting, specifically mentioning the difficulty the professor had in explaining it. This highlights the importance of clear teaching and understanding in the educational process, especially for complex statistical concepts.
Highlights

Degrees of freedom is a crucial term in statistics, often misunderstood but essential for various calculations.

The concept was challenging to grasp initially, even for the speaker during their introduction to statistics.

Degrees of freedom (DF) is symbolized by the term 'DF' and sometimes represented with dots between the letters.

The formal definition of degrees of freedom is the number of values within a system that are free to vary.

Understanding degrees of freedom can help in reconstructing formulas and solving statistical problems.

An example is used to clarify the concept, involving a distribution of three numbers representing the number of apples people have.

The mean of the distribution is calculated, and deviations from the mean are determined for each person.

Deviations from the mean in a system must sum up to zero, a key rule in variability calculations.

The last value in a system of deviations is not free to vary and is therefore not included in the degrees of freedom.

The general formula for degrees of freedom is n minus 1, where n is the number of values or terms within a distribution.

The concept is that you can figure out all numbers in a distribution except for one, which is restricted.

The degrees of freedom for a system of three numbers is two, as only two numbers can vary freely.

The speaker uses the analogy of assigning arbitrary values to the first two numbers in a system, with the third being determined.

The importance of understanding the concept of degrees of freedom is emphasized for its practical applications in statistics.

The video aims to provide clarity on a concept that is often confusing but fundamental to statistical analysis.

The speaker shares their personal experience of learning about degrees of freedom and the challenges they faced.

The explanation is designed to help viewers build a mental model of degrees of freedom, facilitating a deeper understanding.

The video concludes with a hope that the explanation aids viewers in grasping the concept of degrees of freedom.

Transcripts

Browse More Related Video

Degrees of Freedom Explained

Degrees Of Freedom Explained | What is Degrees of freedom | Degrees of freedom in statistics

what are degrees of freedom?

Standard Deviation & Degrees of Freedom Explained | Statistics Tutorial | MarinStatsLectures

The Sample Variance and its Chi Squared Distribution

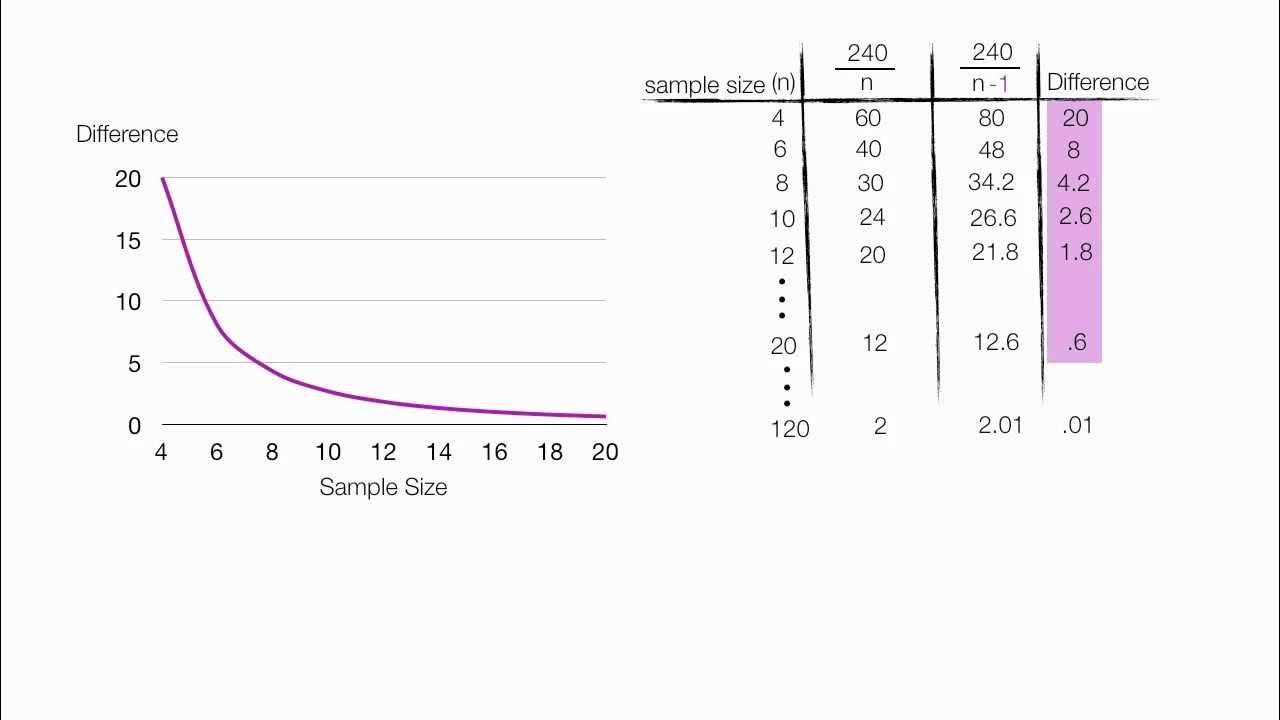
Why are degrees of freedom (n-1) used in Variance and Standard Deviation

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Degrees of FreedomStatisticsEducationVarianceMeanDeviationPsychologyCalculationIntro StatsConcept Clarity