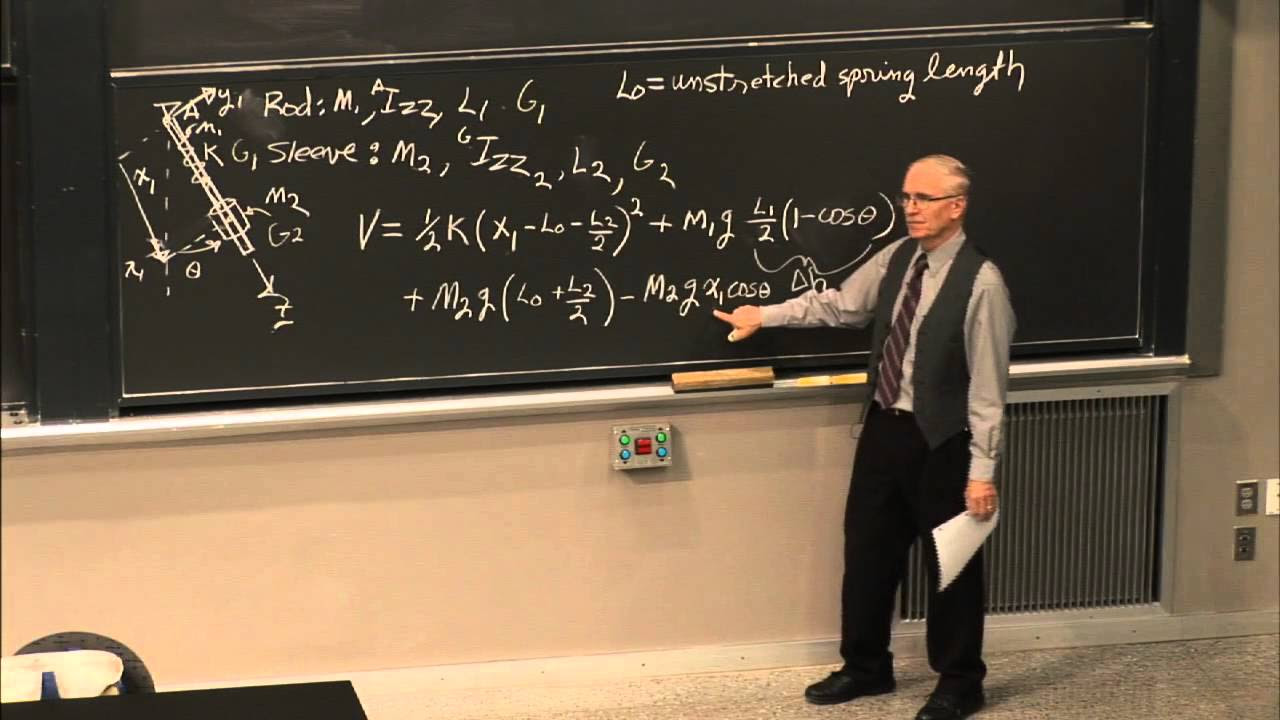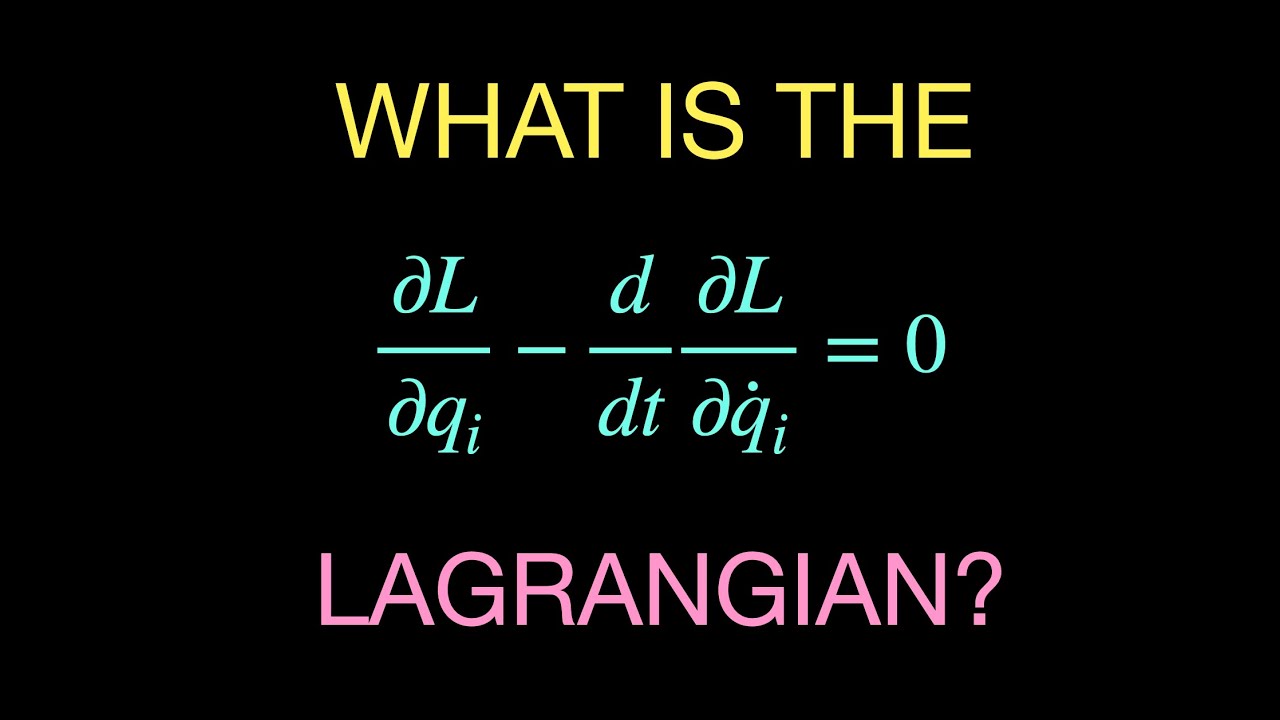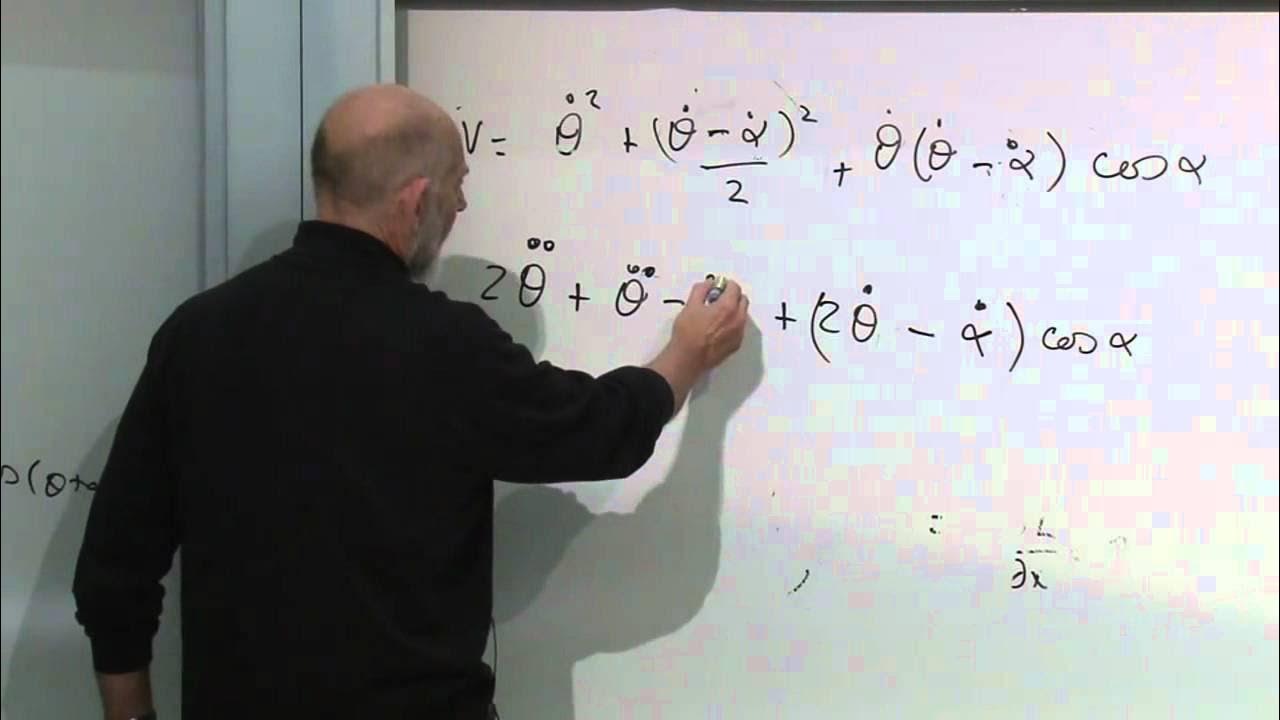Lagrangian Mechanics II: Degrees of freedom, generalized coordinates and a cylinder
TLDRThis video delves into the application of Lagrangian mechanics to solve a complex system, focusing on the concepts of degrees of freedom and generalized coordinates. It uses a cylinder as an example to illustrate the translational and rotational degrees of freedom, highlighting how constraints can reduce these. The video then guides through the process of formulating the Lagrangian for a constrained cylinder pendulum, calculating its kinetic and potential energies, and deriving the equations of motion using Euler-Lagrange equations. The challenge of solving non-linear differential equations is introduced, with a promise of exploring linearization and numerical methods in upcoming videos.
Takeaways
- 📚 The script introduces the concept of Lagrangian mechanics and its application to complex systems beyond simple one-dimensional cases.
- 🔍 It discusses the importance of understanding degrees of freedom and generalized coordinates in the context of rigid body motion.
- 📏 The video explains that a rigid body, such as a cylinder, has three translational and three rotational degrees of freedom, totaling six.
- 🧩 The concept of constraints is introduced, showing how they can reduce the degrees of freedom in a mechanical system.
- 🔄 The script uses the example of a cylindrical pendulum to illustrate the application of Lagrangian mechanics to constrained systems.
- 📐 It demonstrates how to choose generalized coordinates, such as angles theta 1 and theta 2, to simplify the description of motion.
- 🔧 The video outlines the process of calculating the kinetic and potential energies required to formulate the Lagrangian of the system.
- 📉 The moment of inertia and angular velocity are discussed as key components in calculating the rotational kinetic energy.
- 📚 The Euler-Lagrange equation is applied to derive the equations of motion for the system, highlighting the complexity of non-linear differential equations.
- 🔬 Two methods for solving the equations of motion are mentioned: linearization for small oscillations and numerical integration for more exact solutions.
- 🎥 The script concludes with a teaser for future videos that will focus on solving and interpreting the derived equations of motion.
Q & A
What are the fundamental concepts established in the last video before discussing the Lagrangian approach for a complex system?
-The fundamentals of Lagrangian mechanics were established, including how to obtain equations of motion for a simple one-dimensional system by using the Lagrangian and the Euler-Lagrange equation.
What are degrees of freedom and generalized coordinates in the context of mechanics?
-Degrees of freedom are the minimum number of independent coordinates needed to describe the position and orientation of a system. Generalized coordinates are a set of coordinates that uniquely define the position and orientation of a system, simplifying the description of motion.
How many translational degrees of freedom does a point in three-dimensional space have?
-A point in three-dimensional space has three translational degrees of freedom, as it requires three independent coordinates to describe its position.
Why does a rigid body not have an infinite number of degrees of freedom despite being composed of many atoms?
-A rigid body does not have an infinite number of degrees of freedom because the distances between any two points on the body are assumed to remain constant, which simplifies the description of motion in terms of rotations about a reference point.
How many rotational degrees of freedom does a rigid body have?
-A rigid body has three rotational degrees of freedom, corresponding to the three independent ways it can be rotated about the axes of a coordinate system.
What is the total number of degrees of freedom for a cylinder when considering both translation and rotation?
-A cylinder has a total of six degrees of freedom when considering both translation (three degrees) and rotation (three degrees).
What is a constraint in a mechanical system and how does it affect the degrees of freedom?
-A constraint in a mechanical system is a condition that restricts the motion of the system. Each constraint reduces the number of degrees of freedom by one, as it allows one coordinate to be expressed in terms of others or demands that some coordinate is constant.
How can the motion of a cylinder be described with constraints?
-The motion of a cylinder can be described with constraints such as attaching it to a pivot with a light string of constant length, preventing twisting, and restricting it to swing in a specific plane, which reduces the degrees of freedom.
What is the moment of inertia and why is it important in calculating the kinetic energy of a rotating body?
-The moment of inertia is a measure of how the mass of a body is distributed about an axis of rotation. It is important in calculating the kinetic energy of a rotating body because it quantifies the resistance of the body to changes in its rotational motion.
How is the angular velocity of a rotating cylinder related to the rate of change of its orientation angle?
-The angular velocity of a rotating cylinder is directly related to the rate of change of its orientation angle, as it represents the speed at which the angle changes over time.
What is the Lagrangian and how is it used to derive the equations of motion for a system?
-The Lagrangian is a function that combines the kinetic and potential energies of a system. It is used to derive the equations of motion by applying the Euler-Lagrange equations to the generalized coordinates, resulting in a set of differential equations that describe the system's motion.
What are the two methods mentioned for solving the non-linear differential equations derived from the Lagrangian of a system?
-The two methods mentioned are linearizing the system to obtain an approximate solution for small oscillations, which involves concepts from linear algebra, and numerical integration of the equations to obtain a more exact solution.
Outlines
📚 Introduction to Degrees of Freedom and Generalized Coordinates
This paragraph introduces the fundamental concepts of degrees of freedom and generalized coordinates in the context of Lagrangian mechanics. The discussion begins with the example of a rigid body, specifically a cylinder, and explains how three independent Cartesian coordinates are necessary to describe its position. The center of mass is highlighted as a convenient reference point, and it's noted that three coordinates are needed to define its location and the three possible translational directions. The paragraph then delves into the concept of rotational degrees of freedom, explaining that any arbitrary rotation can be broken down into three basic rotations about the body's axes. The rigidity of the body is emphasized, which reduces the seemingly infinite degrees of freedom to a manageable number by assuming constant distances between points. The paragraph concludes by discussing how constraints in a mechanical system can reduce the degrees of freedom, using the example of a cylindrical pendulum with constraints that limit its motion.
🔍 Exploring Generalized Coordinates and Kinetic Energy
In this paragraph, the focus shifts to the selection of generalized coordinates suitable for describing the motion of the cylinder in a constrained system. The concept of generalized coordinates is introduced as a means to uniquely define the position and orientation of the cylinder with just two numbers. The paragraph explains the choice of these coordinates: one for the translation along the circular path (denoted as theta 1) and another for the orientation relative to the vertical (denoted as theta 2). Following this, the kinetic energy of the system is explored, which is divided into translational and rotational components. The moment of inertia, a measure of mass distribution about an axis of rotation, is discussed, along with its calculation for the cylinder. The angular velocity, derived from the rate of change of theta 2, is identified as a key factor in the rotational kinetic energy. The translational kinetic energy is then calculated by determining the velocity of the center of mass, expressed in terms of the chosen angles. The paragraph concludes with a simplified expression for the total kinetic energy, incorporating both translational and rotational components.
📉 Deriving the Lagrangian and Equations of Motion
The final paragraph of the script details the process of formulating the Lagrangian for the constrained cylinder system and deriving the equations of motion. The Lagrangian is constructed by combining the kinetic and potential energies, with the latter calculated based on the mass, gravitational acceleration, and z-coordinate of the center of mass. The paragraph then describes the application of the Euler-Lagrange equations to the chosen generalized coordinates (theta 1 and theta 2). The process involves differentiating the Lagrangian with respect to the angles and their rates of change, leading to a set of differential equations that govern the motion of the system. The paragraph acknowledges the nonlinearity of these equations due to the presence of squares and trigonometric functions, which makes finding exact solutions challenging. Two methods for solving the system are briefly mentioned: linearization for small oscillations and numerical integration for a more exact solution. The paragraph ends with a teaser for future videos that will focus on solving and interpreting these equations.
Mindmap
Keywords
💡Lagrangian Mechanics
💡Euler-Lagrange Equation
💡Degrees of Freedom
💡Generalized Coordinates
💡Rigid Body
💡Center of Mass
💡Moment of Inertia
💡Angular Velocity
💡Kinetic Energy
💡Potential Energy
💡Constraints
Highlights
Introduction to the concept of degrees of freedom and generalized coordinates in the context of Lagrangian mechanics.
Explanation of how a rigid body like a cylinder can be described using three translational and three rotational degrees of freedom.
Discussion on the reduction of degrees of freedom due to constraints in mechanical systems.
Illustration of how a cylindrical pendulum can be constrained to reduce its degrees of freedom.
Introduction of generalized coordinates as a method to simplify the description of complex systems.
Use of angles theta1 and theta2 to describe the position and orientation of the cylinder in a pendulum system.
Decomposition of the kinetic energy of the cylinder into translational and rotational components.
Explanation of the moment of inertia and its role in calculating rotational kinetic energy.
Derivation of the expression for the angular velocity of the cylinder in terms of theta2.
Method to find the velocity of the center of mass by differentiating the position vector.
Simplification of the kinetic energy expression using trigonometric identities.
Calculation of the potential energy of the cylinder based on its position relative to the origin.
Construction of the Lagrangian for the pendulum system using the derived kinetic and potential energy expressions.
Application of the Euler-Lagrange equations to derive the equations of motion for the cylinder.
Introduction of dimensionless constant alpha to simplify the equations of motion.
Challenge of solving non-linear differential equations due to the presence of squares and trigonometric functions.
Proposal of two methods to solve the system: linearization for small oscillations and numerical integration for more exact solutions.
Teaser for upcoming videos that will focus on solving and interpreting the derived equations of motion.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: