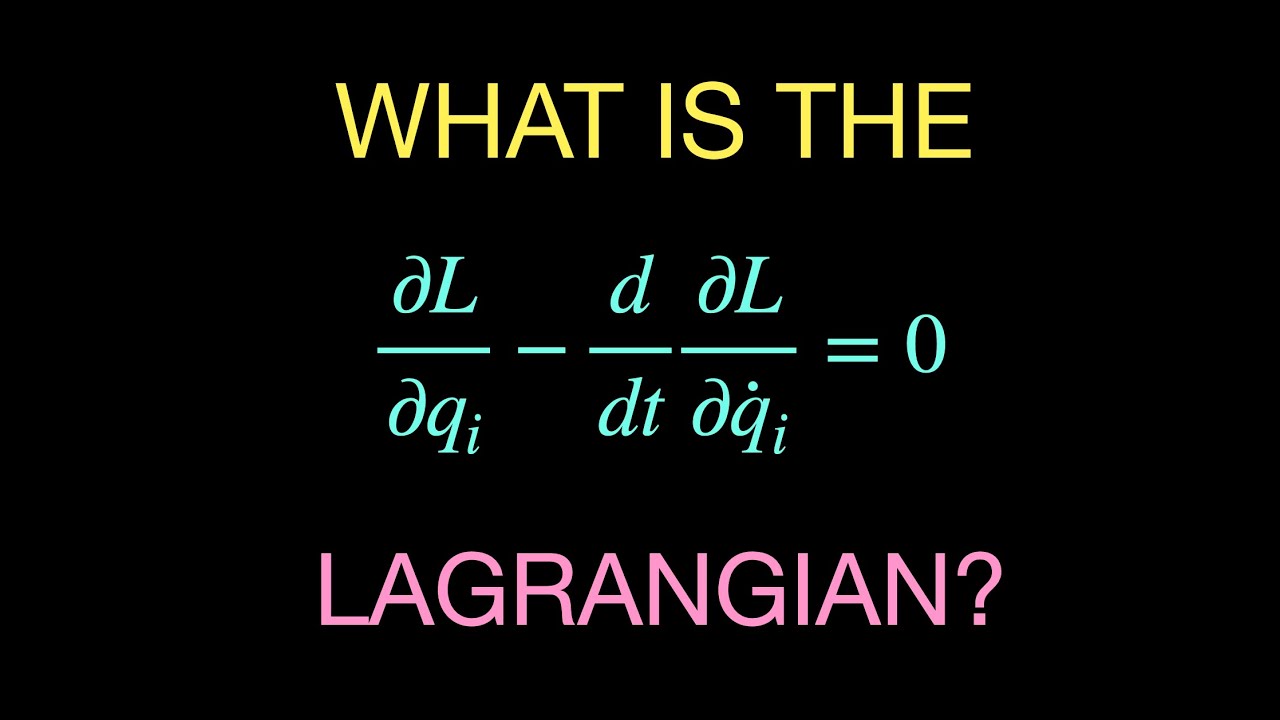Lagrangian and Hamiltonian Mechanics in Under 20 Minutes: Physics Mini Lesson
TLDRIn this physics mini-lesson, Elliott introduces the three formulations of classical mechanics: Newtonian, Lagrangian, and Hamiltonian. Using the simple pendulum as an example, he explains Newton's approach with F=ma, then delves into the Lagrangian method, emphasizing the principle of least action and the Euler-Lagrange equation. Finally, he covers Hamiltonian mechanics, highlighting the phase space and energy conservation, providing a foundation for understanding quantum mechanics and offering animations and problem sheets for deeper exploration.
Takeaways
- 📚 The video introduces three formulations of classical mechanics: Newtonian, Lagrangian, and Hamiltonian mechanics.
- 🔍 Newtonian mechanics, based on F=ma, is taught first but is less used by modern physicists compared to the other two formulations.
- 🌐 Lagrangian and Hamiltonian mechanics are essential for understanding quantum mechanics and the physics of small objects like elementary particles.
- 📏 The simple pendulum is used as an example to illustrate each approach, with the pendulum's motion described using different coordinates.
- 📉 Newton's method involves writing the total force as F=ma, while the Lagrangian approach starts with the kinetic and potential energy.
- 📘 The Lagrangian L is defined as the difference between kinetic and potential energy, and it leads to the Euler-Lagrange equation.
- 📚 The Euler-Lagrange equation is derived from the principle of least action, which states that the actual path of a particle minimizes the action.
- 🔄 The Hamiltonian H is the total energy of the system, and it leads to Hamilton's equations, which are a pair of first-order differential equations.
- 🔄 Hamilton's equations provide a geometric perspective by connecting mechanics to a flow on phase space, where position and momentum define the state of the system.
- 🔗 The Lagrangian and Hamiltonian approaches are not only useful in classical mechanics but are also fundamental to quantum mechanics.
- 🎓 The video encourages viewers to explore these concepts further, offering resources such as notes, animations, and problem sheets for practice.
Q & A
What are the three formulations of classical mechanics mentioned in the video?
-The three formulations of classical mechanics mentioned in the video are Newtonian mechanics, Lagrangian mechanics, and Hamiltonian mechanics.
What is the basic equation used in Newtonian mechanics?
-The basic equation used in Newtonian mechanics is F = ma, which states that the force acting on an object is equal to the mass of the object times its acceleration.
What is the Lagrangian formalism and how does it differ from Newtonian mechanics?
-The Lagrangian formalism is an alternative approach to mechanics that involves writing down the kinetic energy, potential energy, and their difference, known as the Lagrangian. It differs from Newtonian mechanics by using the Euler-Lagrange equation to derive the equations of motion, rather than starting with the total force.
What is the Hamiltonian formalism and how does it relate to the Lagrangian formalism?
-The Hamiltonian formalism is another approach to mechanics that starts with the total energy of the system, known as the Hamiltonian. It relates to the Lagrangian formalism by providing a pair of first-order differential equations for the coordinates and their conjugate momenta, as opposed to the single second-order equation from the Lagrangian.
How does the simple pendulum example illustrate the application of these mechanics?
-The simple pendulum example is used to demonstrate how each formulation of mechanics can be applied to derive the equation of motion for the pendulum. It shows the transition from Newtonian mechanics with F = ma, to the Lagrangian approach using the Euler-Lagrange equation, and finally to the Hamiltonian approach with its first-order equations.
What is the principle of least action and how does it relate to the Euler-Lagrange equation?
-The principle of least action states that of all possible paths a particle could follow, the one it actually chooses is the path that minimizes or extremizes the action, which is the integral of the Lagrangian. The Euler-Lagrange equation is the condition for this action to be minimized, and it is used to derive the equations of motion in the Lagrangian formalism.
Why are Lagrangian and Hamiltonian mechanics important for understanding quantum mechanics?
-Lagrangian and Hamiltonian mechanics are important for understanding quantum mechanics because they provide a framework for transitioning from classical mechanics to quantum mechanics. In quantum mechanics, functions on phase space in classical mechanics turn into operators on the quantum state space, and the Hamiltonian becomes an operator that governs the time evolution of the quantum state.
Outlines
📚 Introduction to Classical Mechanics
In this physics mini-lesson, Elliott introduces the three main formulations of classical mechanics: Newtonian, Lagrangian, and Hamiltonian mechanics. Newtonian mechanics, which is typically taught first, involves applying F=ma to simple systems. The video will focus on the latter two, which are more widely used by modern physicists and are essential for understanding quantum mechanics. The simple pendulum is used as an example to illustrate each approach. Elliott provides a brief review of Newtonian mechanics and encourages viewers to watch a linked video for a more in-depth look at pendulums. The video sets up the stage for a deeper dive into the Lagrangian and Hamiltonian approaches.
🔍 Exploring Lagrangian Mechanics
The second paragraph delves into the Lagrangian formalism of mechanics, which is more mathematically sophisticated than Newton's approach. The Lagrangian L is defined as the difference between kinetic and potential energy. For the pendulum example, the kinetic energy is given by \( \frac{1}{2} m l^2 \theta \dot{}^2 \) and the potential energy by \( -mgl \cos(\theta) \). The Lagrangian is then used to derive the Euler-Lagrange equation, which provides the equation of motion for the system. This approach is advantageous as it does not require dealing with vectors and can handle constraints and symmetries more easily. The paragraph concludes by highlighting the practicality of the Lagrangian method for quickly obtaining equations of motion.
📘 Hamiltonian Mechanics and Phase Space
The third paragraph introduces Hamiltonian mechanics, which starts with the total energy (kinetic plus potential) and defines the Hamiltonian H in terms of position, momentum, and energy. For the pendulum, the Hamiltonian is expressed as \( \frac{p^2}{2ml^2} - mgl \cos(\theta) \). Hamilton's equations are then used to derive a pair of first-order differential equations for position and momentum. This approach provides a geometric perspective on the mechanics of the pendulum, connecting it to a flow on phase space. The energy conservation principle is emphasized, as the system's trajectory in phase space must lie on a line of constant energy. The paragraph concludes with an invitation to explore animations that visualize the phase space flow of the pendulum.
🌐 Conclusion and Further Exploration
In the concluding paragraph, the video summarizes the importance of Lagrangian and Hamiltonian mechanics not only in classical mechanics but also in quantum mechanics. It explains how these classical concepts translate into quantum mechanics, with functions on phase space becoming operators on quantum state spaces. The Schrödinger equation is mentioned, which describes how the state of a quantum system evolves over time using the Hamiltonian operator. The video encourages viewers to explore further, providing links to notes, animations, and problem sheets for practice. It ends with a call to like, subscribe, and comment on topics of interest for future videos.
Mindmap
Keywords
💡Classical Mechanics
💡Newtonian Mechanics
💡Lagrangian Mechanics
💡Hamiltonian Mechanics
💡Euler-Lagrange Equation
💡Phase Space
💡Action
💡Momentum
💡Simple Pendulum
💡Quantum Mechanics
Highlights
Introduction to the three formulations of classical mechanics: Newtonian, Lagrangian, and Hamiltonian mechanics.
Newtonian mechanics is the foundation taught in introductory physics classes, using F=ma for simple systems.
Lagrangian and Hamiltonian mechanics are essential for understanding quantum mechanics and the physics of small objects.
The simple pendulum is used as an example to illustrate each approach in the lesson.
Setting up coordinates to describe the pendulum's position using arc length or angle theta.
Review of Newtonian mechanics applied to the pendulum, including the equation of motion for theta.
Special case of the pendulum's motion when theta is small, resulting in a simple sine or cosine solution.
Introduction of the Lagrangian formalism, starting with kinetic and potential energy.
Derivation of the Euler-Lagrange equation from the Lagrangian, leading to the pendulum's equation of motion.
The principle of least action and its relation to the Euler-Lagrange equation.
Hamiltonian mechanics starting with the total energy and defining the Hamiltonian function.
Hamilton's equations transforming the single second-order differential equation into a pair of first-order equations.
The geometric perspective of mechanics provided by Hamiltonian mechanics and the concept of phase space.
Conservation of energy in the pendulum system and its representation in phase space.
Animations provided to visualize the pendulum's motion and phase space flows.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: