Lagrangian Mechanics: How powerful is it?

The Science Asylum
9 Jul 201910:01
EducationalLearning
32 Likes 10 Comments

TLDRThis episode dives into Lagrangian Mechanics, a powerful alternative to Newtonian mechanics for modeling complex systems like the double pendulum. It explains how Lagrangian Mechanics, which considers the entire path of an object, uses energy concepts like kinetic and potential to predict motion through the principle of stationary action. The video contrasts this approach with Newtonian mechanics and highlights its utility in scenarios where traditional methods fall short, especially in quantum mechanics.

Takeaways
  • 📚 Newtonian mechanics is a fundamental way to model motion based on forces, but it can be complex for systems like the double pendulum.
  • 🔧 Lagrangian Mechanics offers a powerful alternative to Newtonian mechanics, especially for complex systems where Newtonian methods become cumbersome.
  • 🤔 Lagrangian Mechanics was developed by Joseph-Louis Lagrange and is based on the principle of least action, which seeks the path of motion with minimal energy variation.
  • 💡 The concept of 'action' in Lagrangian Mechanics is crucial, representing the efficiency of a path and guiding the principle of stationary action.
  • 🚀 Lagrangian Mechanics considers the entire path of an object rather than just the forces at a single moment, providing a holistic view of motion.
  • 📈 Energy, both kinetic and potential, plays a central role in Lagrangian Mechanics, with the Lagrangian being a scalar quantity combining these energies.
  • 🔍 Lagrangian Mechanics uses generalized coordinates, or 'degrees of freedom,' which are specific to the scenario and simplify the analysis of complex systems.
  • 🌐 Configuration space is an abstract representation used in Lagrangian Mechanics to map out possible configurations of a system, distinct from our 3D physical space.
  • 🔄 The principle of stationary action states that objects follow the path with the least variation in action, not necessarily checking all paths.
  • 🛠 Both Newtonian and Lagrangian Mechanics are tools for predicting motion, with the choice of method depending on the complexity and nature of the system.
  • 🌐 Lagrangian Mechanics is particularly useful in quantum mechanics, where the concept of force is less defined, and it provides a bridge to more abstract physical theories.
Q & A

  • What is Lagrangian mechanics, and how does it differ from Newtonian mechanics?

    -Lagrangian mechanics is a method in physics for predicting the path an object will take by considering the entire path at once and focusing on the energy of the system rather than forces. Unlike Newtonian mechanics, which relies on step-by-step calculations using forces, Lagrangian mechanics uses the concept of stationary action, where the actual path an object takes minimizes the variation in action, a quantity derived from kinetic and potential energies.

  • Why might Newtonian mechanics be less suitable for complex systems like a double pendulum?

    -Newtonian mechanics becomes challenging for complex systems like a double pendulum because it requires tracking multiple changing forces over time, which can lead to chaotic behavior where small differences in initial conditions result in vastly different outcomes. This complexity makes it difficult to predict motion accurately using Newton's laws alone.

  • What is the principle of stationary action in Lagrangian mechanics?

    -The principle of stationary action states that the path taken by an object between two points is the one that minimizes the variation in a quantity called 'action,' which is a measure of the efficiency of a path based on the Lagrangian, a combination of kinetic and potential energy.

  • Why does Lagrangian mechanics use generalized coordinates, and what are they?

    -Lagrangian mechanics uses generalized coordinates, or degrees of freedom, to simplify the description of a system's motion. These coordinates are specific to the system being analyzed and are not necessarily the standard three-dimensional spatial coordinates. For example, a simple pendulum's motion can be described by the angle of its string, which is a single degree of freedom.

  • How does the concept of 'action' help in predicting the motion of an object?

    -The concept of action helps in predicting motion by providing a way to evaluate different possible paths an object could take. The path with the least variation in action is the one the object will follow. This approach allows for a more holistic view of motion, especially in complex systems where forces are difficult to track.

  • What historical developments led to the creation of Lagrangian mechanics?

    -Lagrangian mechanics was developed by Joseph-Louis Lagrange in 1788, building on earlier ideas from Pierre de Fermat, who proposed that light follows the path of least time, and even earlier contributions from ibn al-Haytham in the 11th century. Lagrange expanded these ideas to matter, leading to the formulation of Lagrangian mechanics.

  • What role does energy play in Lagrangian mechanics?

    -In Lagrangian mechanics, energy is central to understanding motion. The Lagrangian is a combination of kinetic energy (associated with motion) and potential energy (associated with position). The variation of this Lagrangian over a path is what determines the action, guiding the object's motion along the path of least variation in energy.

  • Why isn't Lagrangian mechanics used all the time if it's so powerful?

    -Lagrangian mechanics is not always used because it is often more complex than necessary for simple systems. Newtonian mechanics is usually sufficient for straightforward scenarios where forces and motion are easy to track. Lagrangian mechanics is more useful for systems where forces are complex or where energy considerations provide a clearer understanding.

  • How does Lagrangian mechanics apply to quantum mechanics?

    -In quantum mechanics, where the concept of force becomes less meaningful, Lagrangian mechanics provides a useful framework. It allows for the consideration of all possible paths a particle might take, with the actual path being the one that minimizes the variation in action, making it a powerful tool in the quantum realm.

  • What is a configuration space in the context of Lagrangian mechanics?

    -A configuration space is an abstract space used in Lagrangian mechanics to represent all possible configurations of a system. Each point in this space corresponds to a specific set of generalized coordinates, or degrees of freedom. For example, the configuration space for a double pendulum would be a two-dimensional grid representing the angles of the two pendulum strings.

Outlines
00:00
📚 Introduction to Lagrangian Mechanics

This paragraph introduces the concept of Lagrangian Mechanics as an alternative to Newtonian mechanics for modeling complex systems like the double pendulum. It explains that mechanics is a branch of physics dealing with motion and highlights different methods to predict object paths, including Newtonian, Lagrangian, Hamiltonian, and quantum mechanics. The paragraph emphasizes the usefulness of each method in different scenarios and introduces the double pendulum as an example of a system too complicated for Newtonian mechanics. It also mentions the historical development of these ideas, referencing Fermat and ibn al-Haytham, and introduces the Lagrangian, a combination of kinetic and potential energy, as a key concept in this approach.

05:02
🔍 Exploring the Principle of Stationary Action

The second paragraph delves into the principle of stationary action, which is central to Lagrangian Mechanics. It explains how objects follow the path with the smallest variation in action, which is related to energy and work. The paragraph uses the analogy of a graph to illustrate stationary points and how the principle helps in predicting the path an object will take. It clarifies that while Lagrangian mechanics considers the entire path, it is still a tool for prediction and does not imply that the object itself evaluates all possible paths. The summary also touches on the use of generalized coordinates or degrees of freedom in Lagrangian mechanics, contrasting it with the three-dimensional position-space of Newtonian mechanics. It concludes by discussing the applicability of Lagrangian mechanics in various scenarios, including its utility in quantum mechanics where the concept of force is less defined.

Mindmap
Keywords
💡Lagrangian Mechanics
Lagrangian mechanics is a reformulation of classical mechanics introduced by Joseph-Louis Lagrange in 1788. It provides a powerful alternative to Newtonian mechanics by focusing on energy rather than forces. In the video, it's used to explain the motion of complex systems, such as a double pendulum, where forces become complicated to track. Lagrangian mechanics considers the entire path an object might take, making it particularly useful for systems where forces are difficult to quantify.
💡Newtonian Mechanics
Newtonian mechanics is the classical theory of motion formulated by Sir Isaac Newton. It relies on forces to predict the motion of objects, following Newton's laws of motion. In the video, it's highlighted as the go-to method for simple scenarios, like the motion of a single pendulum. However, its complexity increases significantly in systems with multiple interacting forces, such as a double pendulum. Newtonian mechanics works on a cause-and-effect basis, making it suitable for systems where forces are straightforward and easily calculated.
💡Double Pendulum
A double pendulum consists of two pendulums attached end-to-end, and it's known for its complex and chaotic motion. In the video, it's described as a 'beast' due to the unpredictable paths it can take, highlighting the challenges of using Newtonian mechanics to model its motion. The double pendulum is a classic example in chaos theory, where slightly different initial conditions can lead to drastically different outcomes. Lagrangian mechanics is suggested as a more efficient approach to understanding its behavior by focusing on the system's energy rather than individual forces.
💡Kinetic Energy
Kinetic energy is the energy associated with the motion of an object. In the video, it's described as a major category of energy considered in Lagrangian mechanics, alongside potential energy. Kinetic energy is defined as the scalar version of velocity, which is a vector quantity. In the context of Lagrangian mechanics, kinetic energy contributes to the calculation of the Lagrangian, a key component in determining the most efficient path an object will take.
💡Potential Energy
Potential energy is the energy associated with an object's position or configuration. In the video, it's presented as the second major category of energy in Lagrangian mechanics, complementing kinetic energy. Potential energy is the scalar version of position, a vector quantity. Lagrangian mechanics combines both kinetic and potential energy to form the Lagrangian, which is used to find the path of least variation in action, allowing predictions of motion without directly considering forces.
💡Principle of Stationary Action
The principle of stationary action, also known as the principle of least action, states that the path taken by a physical system between two states is the one with the smallest variation in action. Action is a quantity derived from the Lagrangian, representing the efficiency of a path. In the video, this principle is central to understanding Lagrangian mechanics, where the goal is to find the path with minimal variation, as opposed to predicting each step through forces, as done in Newtonian mechanics.
💡Configuration Space
Configuration space is an abstract representation of all possible states or positions of a system. In the video, it's explained as a conceptual tool used in Lagrangian mechanics to represent degrees of freedom for systems like pendulums. Each point in this space corresponds to a specific configuration of the system, such as the angles of a double pendulum. Configuration space provides a visual framework to analyze complex systems by mapping out possible configurations rather than focusing on three-dimensional space, which is typical in Newtonian mechanics.
💡Degrees of Freedom
Degrees of freedom refer to the number of independent parameters that define the state of a physical system. In the video, this term is used to describe the specific parameters that determine the motion of systems like pendulums. For example, a simple pendulum has one degree of freedom (the angle of the string), while a double pendulum has two degrees of freedom (the angles of both strings). In Lagrangian mechanics, degrees of freedom are essential for determining the configuration space and understanding the system's dynamics.
💡Chaos Theory
Chaos theory studies systems where small differences in initial conditions can lead to vastly different outcomes. The video highlights the double pendulum as a quintessential example of chaotic behavior, where predicting its motion using Newtonian mechanics becomes increasingly difficult due to its sensitivity to initial conditions. Chaos theory underscores the complexity and unpredictability inherent in certain physical systems, illustrating why alternative methods like Lagrangian mechanics are often necessary for understanding their behavior.
💡Scalar Quantity
A scalar quantity is a physical quantity described by magnitude alone, without direction. In the video, energy is described as a scalar quantity, contrasting with vector quantities like force, velocity, and position. Lagrangian mechanics utilizes scalar quantities, such as kinetic and potential energy, to simplify the analysis of complex systems by focusing on energy distribution across possible paths. Scalars play a crucial role in forming the Lagrangian and determining the principle of stationary action, providing a different approach to modeling motion compared to Newtonian mechanics.
Highlights

Introduction of Lagrangian Mechanics as a powerful alternative to Newtonian mechanics for complex systems like a double pendulum.

Explanation of how Newtonian mechanics is effective for simple scenarios with clear forces but becomes complicated with systems like the double pendulum.

The double pendulum is introduced as a quintessential example of chaos theory, where small changes in initial conditions lead to vastly different outcomes.

Lagrangian Mechanics was developed by Joseph-Louis Lagrange in 1788, offering a new way to analyze physical systems by considering the entire path of motion rather than just cause and effect.

Comparison between Newtonian mechanics, which uses forces to predict motion step-by-step, and Lagrangian mechanics, which looks for patterns by considering energy and work.

Introduction to Fermat's principle, which influenced Lagrange's thinking by suggesting that light takes the path requiring the least time, hinting at a broader pattern in physical paths.

Lagrangian mechanics combines kinetic and potential energy into a single quantity called the Lagrangian, which is used to find the most efficient path, known as the path of least action.

Explanation of the principle of stationary action, where the object takes the path with the smallest variation in action, a key concept in Lagrangian mechanics.

Discussion on the use of generalized coordinates (or degrees of freedom) in Lagrangian mechanics, which helps visualize motion in complex systems like the double pendulum.

Comparison of configuration space in Lagrangian mechanics with the traditional three-dimensional position-space used in Newtonian mechanics.

Highlighting that while Newtonian mechanics considers a single moment in time, Lagrangian mechanics considers the path as a whole between two events.

Lagrangian mechanics is particularly useful in quantum mechanics, where the concept of force becomes less meaningful, making it a versatile tool for different physical scenarios.

Emphasis on Lagrangian mechanics being just another tool, with the choice to use it depending on the complexity of the system being analyzed.

The video concludes by inviting viewers to share their thoughts on Lagrangian mechanics and encourages further learning through resources like Brilliant.org.

Brilliant.org is promoted as a resource for learning problem-solving skills in science and math, including courses on classical mechanics that cover Lagrangian mechanics.

Transcripts

Browse More Related Video

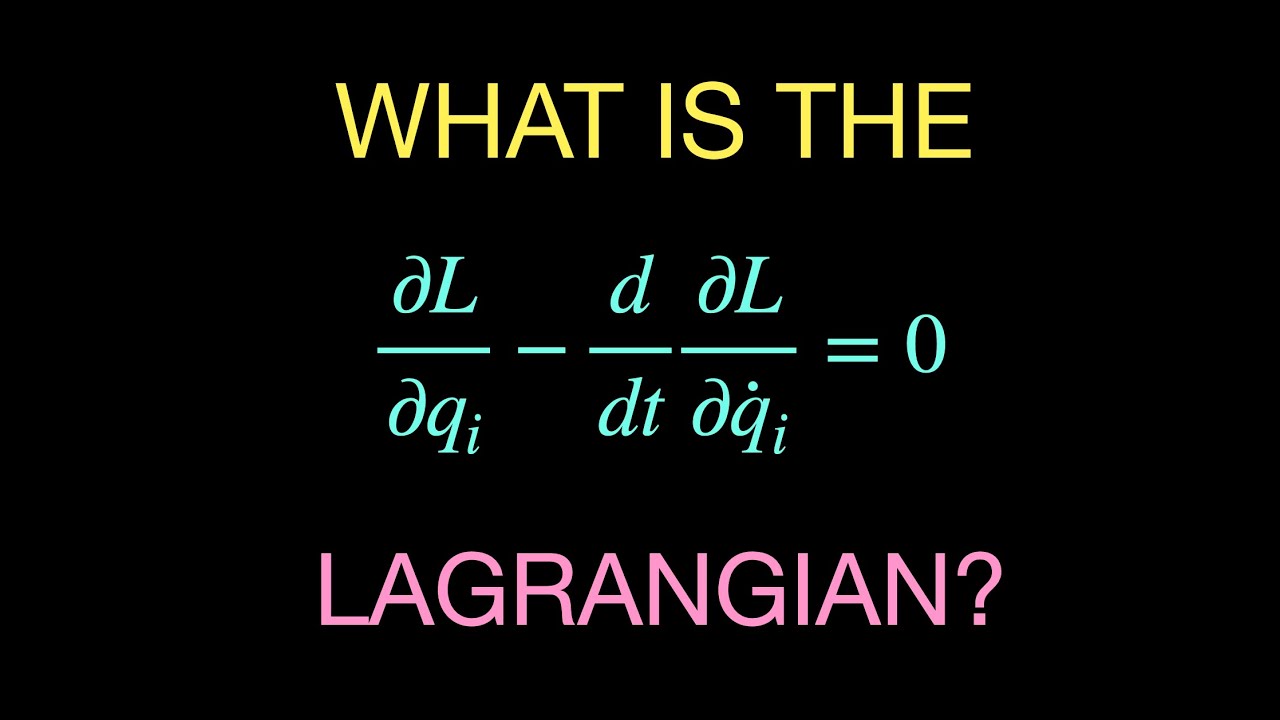
Introduction to Lagrangian Mechanics

Lagrangian and Hamiltonian Mechanics in Under 20 Minutes: Physics Mini Lesson

Ch 12: What are generators in classical mechanics? | Maths of Quantum Mechanics

Lagrangian Mechanics II: Degrees of freedom, generalized coordinates and a cylinder

Explaining the Principle of Least Action: Physics Mini Lesson

How Feynman did quantum mechanics (and you should too)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Lagrangian MechanicsNewtonian PhysicsPhysics EducationMotion AnalysisDouble PendulumChaos TheoryEnergy PrinciplesMechanical SystemsClassical MechanicsProblem Solving