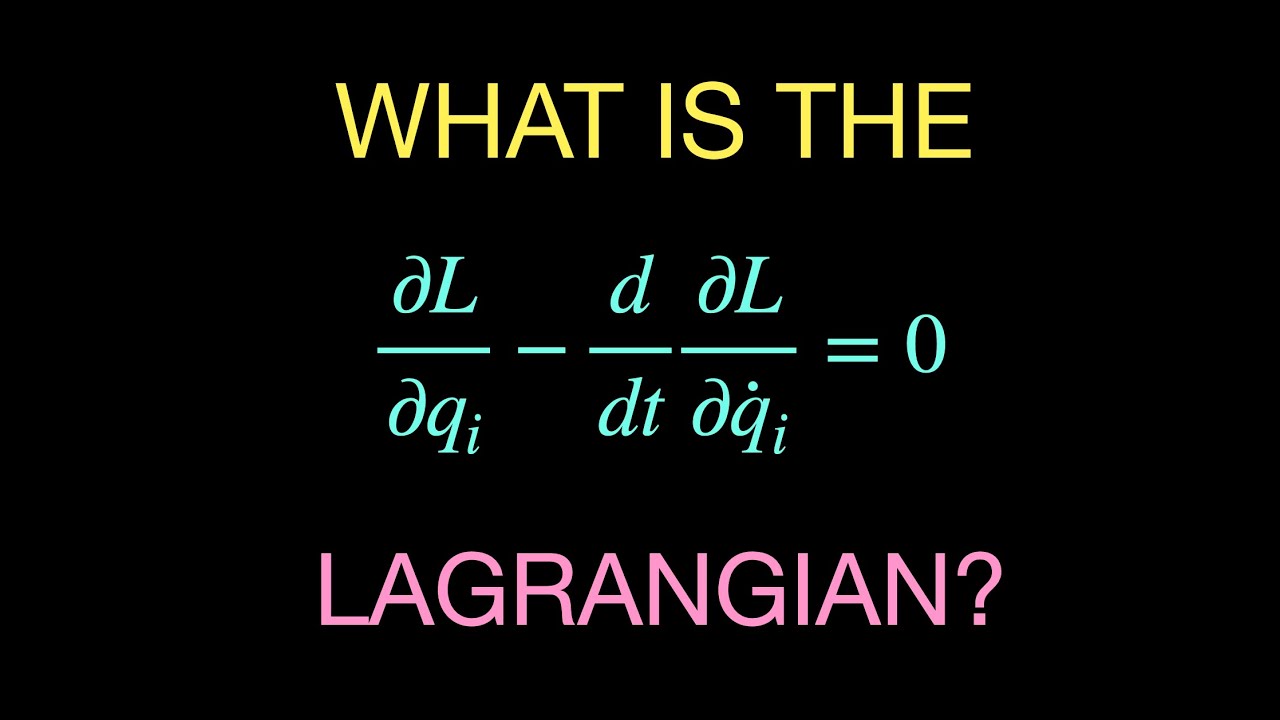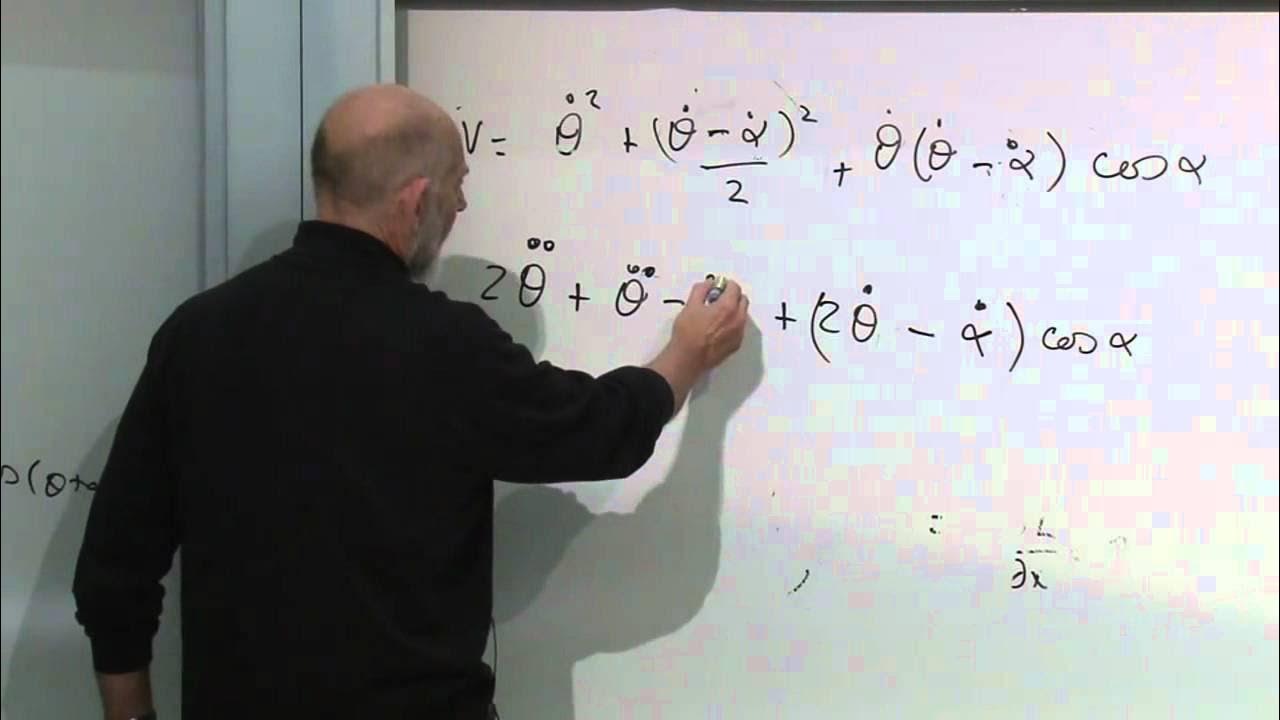15. Introduction to Lagrange With Examples
TLDRThe lecture delves into the Lagrangian method for formulating equations of motion, emphasizing generalized coordinates and forces. It covers the derivation of the Lagrangian equations for systems with multiple degrees of freedom, using examples like a mass-spring-damper system and a complex pendulum-slider system. The professor illustrates how to apply the method systematically, including calculating kinetic and potential energies, and identifying generalized forces through virtual work. The discussion also touches on the importance of verifying the coordinates' completeness, independence, and holonomicity for the Lagrangian approach to be applicable.
Takeaways
- 📚 The lecture introduces the Lagrange method, which is essential for formulating equations of motion using generalized coordinates and forces.
- 🔍 The importance of reading the supplementary notes on the Lagrange method on Stellar is emphasized for a deeper understanding.
- 🗓 The second quiz is scheduled for November 8, following the same format as the first, indicating a consistent assessment approach.
- 📘 The Lagrangian is defined as the difference between the total kinetic energy (T) and potential energy (V) of a system, which is central to the method.
- 🔑 Generalized coordinates (qj) and forces (Qj) are introduced, with the former being variables describing the system's configuration and the latter being non-conservative forces acting on the system.
- 🌐 The Lagrange equation is explained as a means to derive equations of motion, highlighting its application for systems with multiple degrees of freedom.
- 📐 The concept of generalized coordinates being independent and complete is discussed, which is necessary for the system to be holonomic.
- 🔄 The process of deriving Lagrange's equations involves calculating four specific terms related to kinetic and potential energy, as well as generalized forces.
- 📉 For mechanical systems, potential energy is not a function of time or velocity, simplifying the Lagrange equations for such cases.
- 🛠️ Practical application of the Lagrange equations is demonstrated through step-by-step examples, including a mass-spring-damper system and a more complex multi-degree of freedom system.
- 🤔 The lecture concludes with an interactive session where students are encouraged to predict the acceleration terms that would appear in the equations of motion for a given system, fostering deeper engagement with the material.
Q & A
What is the main topic of the lecture?
-The main topic of the lecture is the Lagrange method, which is used for formulating equations of motion in classical mechanics.
What is the Lagrangian in the context of the Lagrange method?
-The Lagrangian, denoted as L, is defined as the difference between the kinetic energy (T) and the potential energy (V) of a system, i.e., L = T - V.
What are generalized coordinates and generalized forces in the context of the Lagrange method?
-Generalized coordinates (qj) are variables used to describe the configuration of a system, and generalized forces (Qj) are the forces associated with changes in these coordinates.
What does the Lagrange equation represent?
-The Lagrange equation represents the dynamics of a system. It states that the time derivative of the partial of the Lagrangian with respect to the generalized velocities (qj dots) minus the partial derivative with respect to the generalized displacements equals the generalized forces.
What are the conditions that generalized coordinates must satisfy?
-Generalized coordinates must be independent, complete, and the system must be holonomic. This means that they should not be constrained by each other, must be able to describe the system at all times, and the number of coordinates should match the degrees of freedom.
What is the significance of the term 'holonomic' in the context of generalized coordinates?
-A system is holonomic if the number of degrees of freedom required is equal to the number of coordinates needed to describe the motion completely.
How does the potential energy term in the Lagrange equation behave for mechanical systems?
-For mechanical systems, the potential energy is not a function of time or velocity, which simplifies the Lagrange equation by eliminating certain terms.
What is the practical approach to using the Lagrange equations as described by the professor?
-The practical approach involves identifying the kinetic and potential energies, calculating the partial derivatives with respect to the generalized coordinates and velocities, and then summing them up to form the equations of motion.
What is the procedure for solving a problem using the Lagrange method?
-The procedure involves determining the degrees of freedom, choosing appropriate generalized coordinates, verifying their independence, completeness, and holonomicity, computing the kinetic and potential energies, and then applying the Lagrange equations to derive the equations of motion.
Can you provide an example of a non-holonomic system from the lecture?
-An example of a non-holonomic system is a ball rolling on a plane without slipping. It requires more coordinates (x, y, and orientation) than the degrees of freedom to describe its motion.
What is the importance of virtual work in the context of the Lagrange method?
-Virtual work is used to calculate the generalized forces associated with non-conservative forces in the system. It helps in determining the right-hand side of the Lagrange equation for each generalized coordinate.
How does the lecture illustrate the application of the Lagrange method to a complex system?
-The lecture uses a complex system involving a rod and a sliding sleeve with multiple degrees of freedom. It demonstrates the process of identifying coordinates, calculating energies, and applying the Lagrange method to derive the equations of motion.
What are the steps involved in deriving the equations of motion for a system with two degrees of freedom?
-The steps include identifying the two generalized coordinates, calculating the kinetic and potential energies for each coordinate, applying the Lagrange equations for each coordinate to get two separate equations, and then solving these equations to describe the system's motion.
What are the different types of kinetic energy that need to be considered for a system with both rotational and translational motion?
-The different types of kinetic energy include rotational kinetic energy associated with each rigid body (rod and sleeve), translational kinetic energy associated with the movement of the center of mass of the sliding mass, and the kinetic energy due to the velocity of the center of mass in the inertial frame.
How is the potential energy of the spring calculated in the given system?
-The potential energy of the spring is calculated as half the spring constant (k) times the square of the total stretch, which is the difference between the current position (x1) and the sum of the unstretched spring length (l0) and half the length of the rod (l1).
What is the difference between the kinetic energy expressions for the rod and the sleeve?
-The kinetic energy expression for the rod accounts for the rotational kinetic energy about point A and the translational kinetic energy of the center of mass. For the sleeve, the kinetic energy expression includes the rotational kinetic energy about its center of mass (g2) and the translational kinetic energy due to its movement along the rod.
Why is the term 'Eulerian acceleration' mentioned in the context of the theta equation of motion?
-The Eulerian acceleration term, represented by theta double dot, is expected in the theta equation of motion because it represents the acceleration experienced by the system during its swinging motion, which is a rotational motion.
What is the physical significance of the terms in the x1 equation of motion derived in the lecture?
-The terms in the x1 equation of motion represent the force components acting on the sliding mass. These include the linear acceleration term (mx1 double dot), the centripetal acceleration term (m2 x1 theta dot squared), the spring force (k x1), and the component of gravity (m2g cosine theta).
How can you verify the correctness of the derived equations of motion?
-The correctness of the derived equations of motion can be verified by checking if they align with Newtonian physics, satisfy the laws of statics, and make sense physically, such as including expected acceleration terms and forces.
Outlines
📚 Introduction to Lagrange's Method
The script begins with an introduction to the Lagrange method, emphasizing its importance in physics and engineering. It mentions the Creative Commons license under which the content is provided and encourages donations to MIT OpenCourseWare. The professor outlines the topics for the day, including generalized coordinates and forces, and recommends a set of notes on Stellar for further reading. The lecture also covers the structure of the upcoming quiz and introduces the concept of the Lagrangian, which is the difference between the kinetic and potential energy of a system. The importance of understanding generalized coordinates and forces is highlighted, and the lecture notes their relevance in formulating the Lagrange equations.
🔍 Understanding Lagrange Equations
This paragraph delves deeper into the practical application of Lagrange equations. It explains the simplification of the equations for mechanical systems where potential energy is not a function of time or velocity. The professor emphasizes the importance of bookkeeping in Lagrange's method and introduces the concept of generalized coordinates being independent and complete for a holonomic system. The explanation includes a practical approach to writing down the equations and the process of identifying the correct coordinates for a system, such as a double pendulum, to ensure they meet the criteria of independence and completeness.
📐 Generalized Coordinates and Holonomic Systems
The script continues with a detailed discussion on the selection of generalized coordinates and the concept of holonomic systems. It uses the example of a double pendulum to illustrate the independence and completeness of coordinates and contrasts it with an incorrect choice of coordinates using Cartesian coordinates. The importance of the system being holonomic is highlighted, meaning the number of degrees of freedom equals the number of coordinates needed to describe the system's motion. A counterexample of a non-holonomic system involving a rolling ball with constraints is provided to demonstrate the difference.
🔧 Practical Application of Lagrange's Equations
The professor moves on to the practical application of Lagrange's equations, breaking down the process into systematic steps. These steps include determining the number of degrees of freedom, choosing appropriate coordinates, verifying their completeness, independence, and holonomicity, and computing the kinetic and potential energies for each coordinate. The paragraph also discusses the calculation of generalized forces through virtual work, using a simple mass-spring-damper system as an example to demonstrate the process.
🌟 Advanced Application: Multiple Degrees of Freedom
This section introduces a more complex problem involving multiple degrees of freedom, specifically a steel pipe system with a pendulum and a sliding sleeve. The challenge involves determining the appropriate coordinates to describe the system's motion, which is identified as two: an angle and a deflection. The paragraph outlines the need to calculate potential and kinetic energies for this system, considering the constraints of planar motion and the absence of certain degrees of freedom.
📘 Equations of Motion for a Complex System
The script presents the process of deriving the equations of motion for the complex system introduced earlier. It involves calculating the potential and kinetic energies, taking into account the system's geometry and the forces acting upon it. The potential energy calculation is detailed, considering the unstretched length of the spring and the gravitational potential energy for both the rod and the sleeve. The kinetic energy is broken down into rotational and translational components, with specific attention given to the moving parts of the system.
🔄 Lagrange's Method for a Coupled System
This paragraph continues the application of Lagrange's method to the coupled system, focusing on the derivation of the equations of motion. It discusses the need to apply the method to each coordinate, resulting in two equations for the system. The first equation is developed for the translational motion of the sliding sleeve, and the paragraph outlines the expected acceleration terms, such as the centripetal acceleration and the effects of the spring force and gravity.
📐 Validating the Equations of Motion
The script emphasizes the importance of validating the derived equations of motion against Newtonian physics principles. It suggests checking for the presence of expected acceleration terms and ensuring the equations make sense physically. The paragraph also introduces the concept of static equilibrium as a method to verify the equations, showing that at rest, the forces and torques balance out according to the system's geometry and the forces acting upon it.
🌀 Deriving the Swinging Motion Equation
The final part of the script focuses on deriving the second equation of motion for the swinging motion of the system. It prompts the audience to predict the types of acceleration terms that would appear in this equation, such as the Eulerian acceleration term due to the swinging motion and the Coriolis term resulting from the interaction between the sliding motion and the swinging motion. The paragraph outlines the process of finding these terms by considering the system's kinetic and potential energies and the work done by external forces.
Mindmap
Keywords
💡Lagrange Method
💡Generalized Coordinates
💡Generalized Forces
💡Degrees of Freedom
💡Holonomic
💡Kinetic Energy
💡Potential Energy
💡Virtual Work
💡Equations of Motion
💡Non-Conservative Forces
💡Bookkeeping
Highlights
Introduction to the Lagrange method and its significance in physics and engineering.
Explanation of generalized coordinates and generalized forces in the context of the Lagrange equations.
The importance of reading the supplementary notes on Stellar for a deeper understanding of the Lagrange method.
Details on the second quiz date and format, emphasizing the importance of preparation.
The practical approach to using Lagrange equations, including the calculation of kinetic and potential energies.
Clarification on the conditions under which potential energy is not a function of time or velocity in mechanical systems.
The concept of independence and completeness of generalized coordinates and the system's holonomicity.
Illustration of how to choose appropriate coordinates for a system using the example of a double pendulum.
Discussion on the difference between Cartesian coordinates and generalized coordinates in system description.
The process of deriving the equations of motion using the Lagrange method for a mass-spring-damper system.
Identification of non-conservative forces and their role in the Lagrange equations through virtual work.
A step-by-step guide on setting up and solving a multi-degree of freedom problem using the Lagrange method.
The application of the Lagrange method to a complex system involving a steel pipe with an attached spring and pendulum.
Explanation of how to calculate potential and kinetic energy for a system with multiple rigid bodies.
The use of rotating coordinate systems and their impact on the calculation of kinetic energy.
Derivation of the equation of motion for a single degree of freedom system using the Lagrange method.
Transition to a more complex problem involving a system with both translational and rotational motion.
Final remarks on the importance of verifying the physical accuracy and consistency of derived equations of motion.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: