Separable Differential Equation (Natural Logs)

turksvids
3 May 201304:39
EducationalLearning
32 Likes 10 Comments

TLDRThe speaker in the transcript discusses the common mistakes people make when solving separable differential equations involving natural logarithms. They emphasize the importance of exponentiating before solving for the constant C, as it simplifies the process and eliminates the need to deal with absolute values. Two examples are provided to illustrate the method. In the first, the differential equation involves (y - 3) and the constant multiple 6, leading to the solution y = 3 + 2e^{6x} after applying the technique. The second example involves a negative coefficient for y, which the speaker addresses by factoring out a negative and using u substitution. The key takeaway is to exponentiate before solving for C and to factor out negatives to simplify the coefficient of y, making the problem more manageable.

Takeaways
  • 📚 **Separable Differential Equations**: The speaker discusses separable differential equations, particularly those involving natural logs.
  • 🔍 **Constant Multiples**: When dealing with a constant multiple, it's best to leave it on the right-hand side of the equation.
  • ✅ **Separation of Variables**: The process involves separating variables and integrating both sides of the equation.
  • 😕 **Common Pitfall**: People often make mistakes with the absolute value when dealing with natural logs, which the speaker aims to clarify.
  • 📈 **Exponentiation**: Before solving for the constant C, it's recommended to exponentiate both sides of the equation to avoid dealing with absolute values.
  • 🔁 **Solving for C**: The constant C is solved for in different cases, considering the initial conditions of the function y.
  • 🔄 **Initial Conditions**: The speaker uses initial conditions (y(0) = 5 and y(0) = -2) to illustrate how to find the constant C.
  • 📉 **Handling Negative Coefficients**: To avoid confusion with negative coefficients, the speaker suggests rewriting the equation to make the coefficient of y positive.
  • 🧮 **U-Substitution**: The speaker mentions the importance of u-substitution and the common oversight of the change in sign when differentiating with respect to u.
  • ➕ **Combining Terms**: It's important to combine like terms, such as adding four to isolate y when necessary.
  • 🚫 **Avoiding Negative Signs**: Clear negative signs before exponentiating to simplify the process.
  • 💡 **Final Solution**: The solution to the differential equation is obtained after exponentiation and solving for C, with the consideration of initial conditions.
Q & A

  • What is the main reason for separating differential equations that involve natural logs?

    -Separating differential equations involving natural logs helps to simplify the integration process and avoid common mistakes that people make when dealing with absolute values.

  • Why is it recommended to leave a constant multiple on the right-hand side when separating differential equations?

    -Leaving a constant multiple on the right-hand side simplifies the integration process and avoids unnecessary complications when dealing with differentials.

  • What is the significance of exponentiating before solving for C in a separable differential equation?

    -Exponentiating before solving for C helps to eliminate the need to deal with absolute values, thus simplifying the process and making it easier to find the constant of integration.

  • How does the absolute value sign affect the solution process of a differential equation?

    -The absolute value sign can complicate the solution process by requiring additional considerations when the value inside the absolute value is negative. Exponentiating the equation helps to avoid this issue.

  • What is the advantage of using a new constant after exponentiating?

    -The new constant, which is the result of exponentiating, can be positive or negative. This flexibility allows us to avoid worrying about the absolute value sign in the original equation.

  • Why is it important to consider the initial conditions when solving for C in a differential equation?

    -Initial conditions provide the necessary boundary values to determine the specific constant of integration (C), which is crucial for finding the particular solution to the differential equation.

  • In the context of the script, why is it suggested to factor out a negative to make the coefficient of Y positive?

    -Factoring out a negative to make the coefficient of Y positive simplifies the equation and makes it easier to apply standard integration techniques without the need for additional substitutions or considerations.

  • What is the common mistake that people make when performing a u-substitution with a negative coefficient?

    -A common mistake is forgetting that if 'u' is a function of 'y' and 'du' is negative 'dy', the negative sign must be included in the integration process, which is often overlooked.

  • Why is it recommended to clear out the negative sign before exponentiating in a differential equation?

    -Clearing out the negative sign before exponentiating simplifies the equation and ensures that the exponentiation process is straightforward and less prone to errors.

  • What is the general approach to solving separable differential equations that lead to natural logs?

    -The general approach involves separating the variables, integrating both sides, exponentiating before solving for the constant of integration, and considering initial conditions to find the particular solution.

  • How does the process of exponentiating the equation help in dealing with the absolute value of y - 3?

    -Exponentiating the equation eliminates the need to consider the absolute value of y - 3, as the exponentiation process inherently accounts for both positive and negative values, thus simplifying the integration.

Outlines
00:00
📚 Solving Separable Differential Equations with Natural Logs

The speaker begins by addressing common mistakes made when solving separable differential equations involving natural logs. They present an example with the equation dy/dx = 6 * |y - 3|, emphasizing the importance of keeping constants on the right-hand side. The speaker then demonstrates how to separate the equation, integrate, and handle the absolute value by exponentiating before solving for the constant C. They also discuss two cases where y(0) is given as 5 and -2, respectively, and how exponentiating simplifies the process. The key takeaway is to exponentiate before solving for C to avoid complications with absolute values.

Mindmap
Keywords
💡Separable Differential Equations
Separable differential equations are a class of differential equations where the variables can be separated into two functions, one of x alone and the other of y alone, which can then be integrated. In the video, the speaker discusses solving these types of equations, which often involve natural logarithms, and provides examples to illustrate the process.
💡Natural Logs
Natural logs, or logarithms to the base e, are a mathematical concept used in calculus and the video's context of differential equations. They are used to describe exponential growth or decay and are integral in solving certain types of equations. The script mentions that people often make mistakes when dealing with natural logs in differential equations.
💡Absolute Value
Absolute value denotes the magnitude of a number without regard to its sign. In the context of the video, the absolute value is used in the differential equations to handle cases where the value of y might be less than a certain threshold, which can complicate the equation. The speaker emphasizes the importance of handling absolute values correctly.
💡Integration
Integration is a fundamental operation in calculus, the reverse process of finding derivatives. It is used in the video to solve differential equations by integrating both sides of the equation after separating the variables. The speaker uses integration to find the solution to the given differential equations.
💡Exponentiation
Exponentiation is the operation of raising a number to the power of another number. In the video, the speaker recommends exponentiating before solving for the constant C when dealing with natural logarithms. This simplifies the equation by eliminating the need to deal with absolute values explicitly.
💡Constant Multiple
A constant multiple refers to a constant value that is multiplied by a variable or expression. In the context of the video, the speaker mentions keeping a constant multiple on the right-hand side of the equation when separating variables, which is a common technique in solving differential equations.
💡Initial Conditions
Initial conditions are specific values assigned to the variables at the start of a problem, often used to find particular solutions to differential equations. The script provides examples where the initial condition y(0) is given, which is then used to solve for the constant C in the general solution.
💡U-Substitution
U-substitution is a method used in calculus to simplify the process of integration by substituting a new variable u for a more complicated expression. The speaker mentions that people often forget to account for the derivative of u when using u-substitution, which is a common mistake when dealing with differential equations.
💡Coefficient of Y
The coefficient of Y refers to the numerical factor multiplying the variable Y in an equation. The speaker in the video discusses the preference for having a positive coefficient of Y to simplify the equation and avoid complications with negative signs during the solving process.
💡Factoring
Factoring is a mathematical technique used to break down an expression into a product of simpler expressions. In the video, the speaker uses factoring to make the coefficient of Y positive, which simplifies the process of solving the differential equation by avoiding negative coefficients.
💡Anti-Derivative
An anti-derivative, also known as an integral, is a function whose derivative is equal to the original function. In the context of the video, finding the anti-derivative is part of the process to solve differential equations, and the speaker emphasizes the importance of exponentiating before finding the anti-derivative when natural logs are involved.
Highlights

The speaker emphasizes the common mistake people make when dealing with separable differential equations involving natural logs.

A strategy is shared to handle constant multiples on the right-hand side by leaving them as is.

The importance of separating the equation and introducing integral signs is discussed.

The absolute value of y - 3 is identified as a common source of confusion.

Exponentiation before solving for C is recommended to simplify the process.

The concept of a new constant post-exponentiation is introduced, which can be positive or negative.

The removal of the absolute value concern after exponentiation is explained.

Two different cases for solving for C are demonstrated using given values for y.

The process of plugging in values to find C is shown for both y(0) = 5 and y(0) = -2.

The advantage of exponentiation in handling absolute values is reiterated.

An alternative method for dealing with negative coefficients of y is presented.

The speaker advises against forgetting to perform a u-substitution when integrating.

The process of multiplying by negative one to clear the negative sign before exponentiation is explained.

The final solution for the differential equation is derived using the discussed methods.

The key takeaway is to exponentiate before solving for C when natural logs are involved.

The importance of factoring out a negative to make the coefficient of y positive is highlighted.

The speaker hopes the explanation is helpful and wishes good luck to the learners.

Transcripts

Browse More Related Video

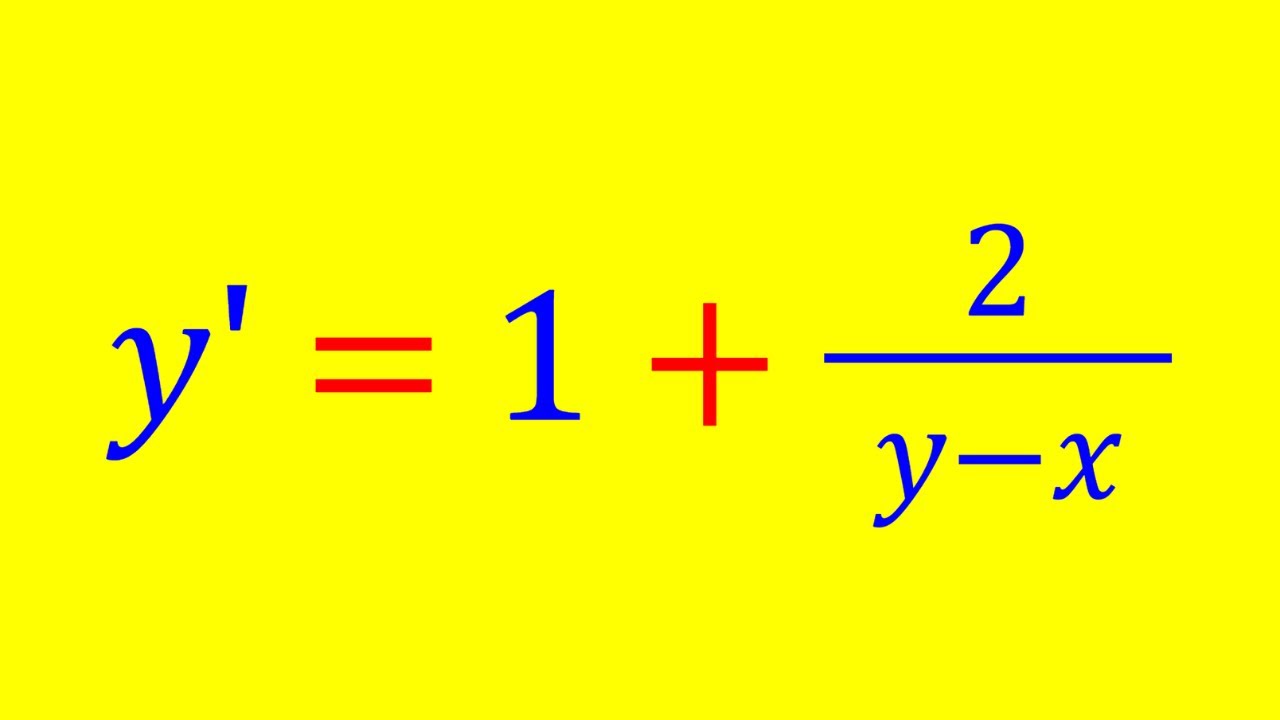
Solving A Non-Linear Differential Equation

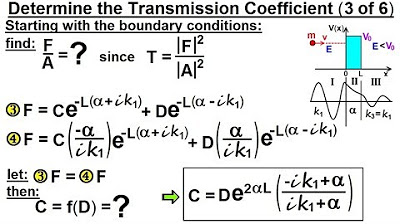
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (85 of 92) Transmission Coeff=? (3 of 6)

Linear Differential Equations & the Method of Integrating Factors

Initial Value Problem

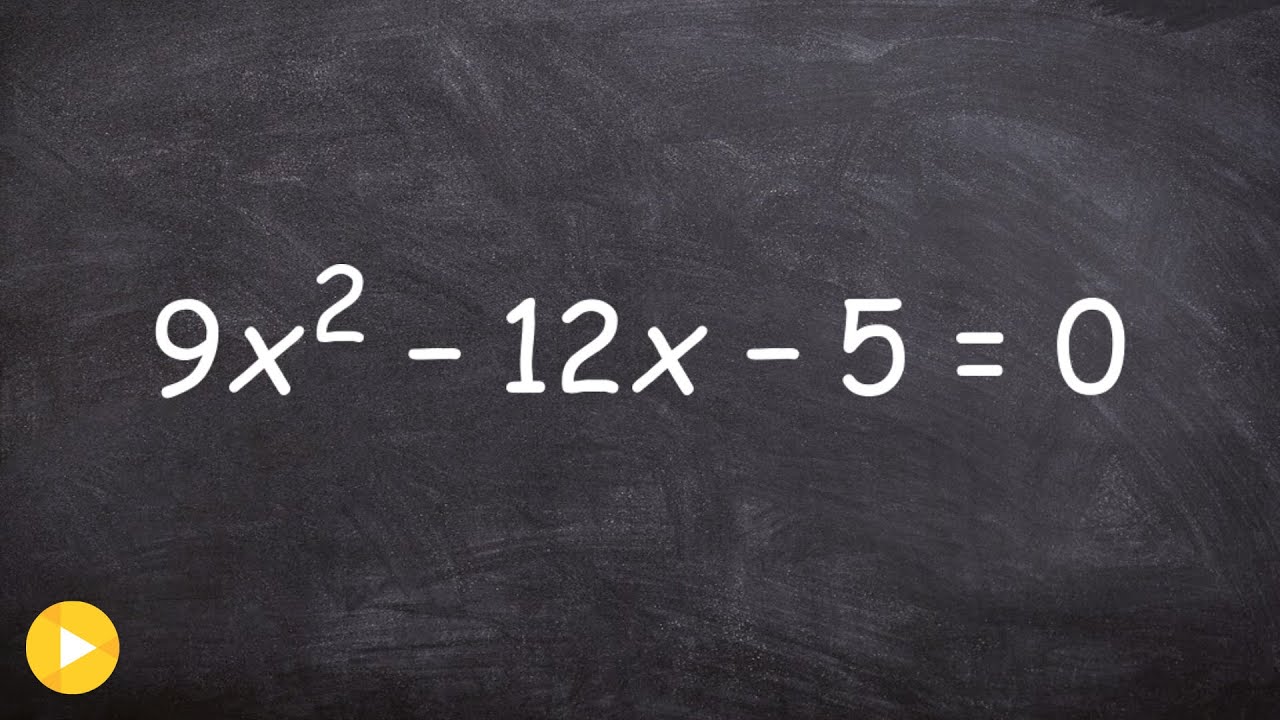
Learn the ac method for factoring and solving a quadratic equation

Definite Integrals from Graphs (Part 2 of 3) - U-Substitution

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Differential EquationsNatural LogsSeparable EquationsMath TutorialAbsolute ValueIntegration TechniquesExponentiationConstant MultipleU-SubstitutionMathematical AnalysisEducational Content