Volumes with Known Cross Sections with Calculus, pg 2

turksvids
30 Sept 202009:50
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the concept of calculating the volume of a solid using calculus, specifically through the method of integrating the area of cross-sections. The presenter emphasizes the importance of expressing the area of a cross-section in terms of the variable of integration, be it x or y. Various shapes such as squares, rectangles, equilateral triangles, and semicircles are covered, each with its own formula for area in terms of a segment 's'. The presenter also highlights the need to memorize certain formulas for quick problem-solving. The script provides a step-by-step approach to solving a problem where the base of the solid is a circle and the cross sections are squares, semicircles, and equilateral triangles. The key takeaway is that once the segment 's' is identified and the appropriate formula is applied, the integration process becomes straightforward. The presenter concludes by encouraging viewers to practice drawing the regions and understanding 's' for success in these types of problems.

Takeaways
  • ๐Ÿ“š To calculate the volume of a solid with a known cross-sectional shape, integrate the area of the cross-section from the start to the end point.
  • ๐Ÿ‘• The speaker humorously mentions changing shirts due to the heat, adding a personal touch to the lecture.
  • ๐Ÿ“ The area of a cross-section must be expressed in terms of the variable of integration, either x or y, depending on the axis it is perpendicular to.
  • ๐Ÿ” Memorizing area formulas for common shapes (squares, rectangles, equilateral triangles, and semicircles) is crucial for these types of problems.
  • ๐Ÿ“ For a rectangle, the area is often expressed as k times s squared, where k is a constant that relates the base and height.
  • โ–ณ The area of an equilateral triangle in terms of the segment s is s squared times the square root of 3 divided by 4.
  • โน For a semicircle, the area is pi over 8 times s squared, where s is the diameter of the semicircle.
  • ๐Ÿ”ณ The volume of a solid with square cross-sections is found by integrating s squared, where s is the side length of the square cross-section.
  • ๐Ÿ”ด The volume of a solid with circular bases and various cross-sectional shapes can be calculated using the integral of the cross-sectional area.
  • ๐Ÿ“ The key to solving these problems is to visualize the region and determine the expression for s, the segment representing the cross-section.
  • ๐Ÿงฎ While a calculator can be used, it's not always necessary as the integrals often simplify to a form that can be solved mentally or with basic arithmetic.
  • ๐ŸŽ“ The process of finding the volume of a solid by integrating cross-sectional areas is a fundamental concept in calculus that should not be intimidating once the principles are understood.
Q & A

  • What are the two primary methods discussed for calculating the volume of an object?

    -The two primary methods discussed are volume by plane slicing and using known cross sections.

  • What is the general approach to finding the volume when you know the cross sections?

    -The general approach is to integrate the area of a cross-section from the starting point to the endpoint.

  • What is the key to solving volume problems using cross sections?

    -The key is to express the area of a cross-section in terms of the variable of integration (x or y).

  • What is the term 's' used to represent in the context of the script?

    -In the script, 's' is used to represent a segment, which is the distance between the top and bottom (or right and left) of a cross-section.

  • What is the formula for the area of a square in terms of 's'?

    -The area of a square in terms of 's' is simply s squared.

  • What is the general formula for the area of a rectangle in terms of 's'?

    -The general formula for the area of a rectangle is k times s squared, where 'k' is a constant that represents the relation between the base and height.

  • What is the formula for the area of an equilateral triangle in terms of 's'?

    -The area of an equilateral triangle in terms of 's' is s squared times the square root of 3, divided by 4.

  • What is the formula for the area of a semicircle in terms of 's'?

    -The area of a semicircle in terms of 's' (where 's' is the diameter) is pi over 8 times s squared.

  • What is the integral formula used to calculate the volume of a solid with square cross sections?

    -The integral formula is the integral from negative 1 to 1 of s squared, where s is 2 root 1 minus x squared.

  • How does the process of calculating the volume of a solid with different cross sections relate to the scale factor?

    -The scale factor is used to adjust the base formula (such as for a square or rectangle) to fit the specific shape of the cross section, like a semicircle or an equilateral triangle.

  • What is the speaker's advice for solving volume problems involving cross sections?

    -The speaker advises to draw the region, figure out what 's' is, and then use the memorized formulas for the area of different shapes to solve the problem.

  • Why does the speaker suggest that one might not need a calculator for these types of problems?

    -The speaker suggests that one might not need a calculator because when you square the expressions for 's', they often simplify to a form that is easy to compute mentally.

Outlines
00:00
๐Ÿ“š Calculus and Volume Calculations

This paragraph discusses the concept of calculating volume using calculus, specifically through plane slicing or known cross sections. The speaker emphasizes the importance of expressing the area of a cross-section in terms of the variable of integration (x or y). The paragraph also covers various area formulas for different shapes such as squares, rectangles, equilateral triangles, and semicircles. The speaker provides a mnemonic for the area of a semicircle as pi over 8 times s squared, where s is the segment representing the diameter of the circle. The focus is on understanding the relationship between the segment and the area of the cross-section to perform the integral for volume calculation.

05:01
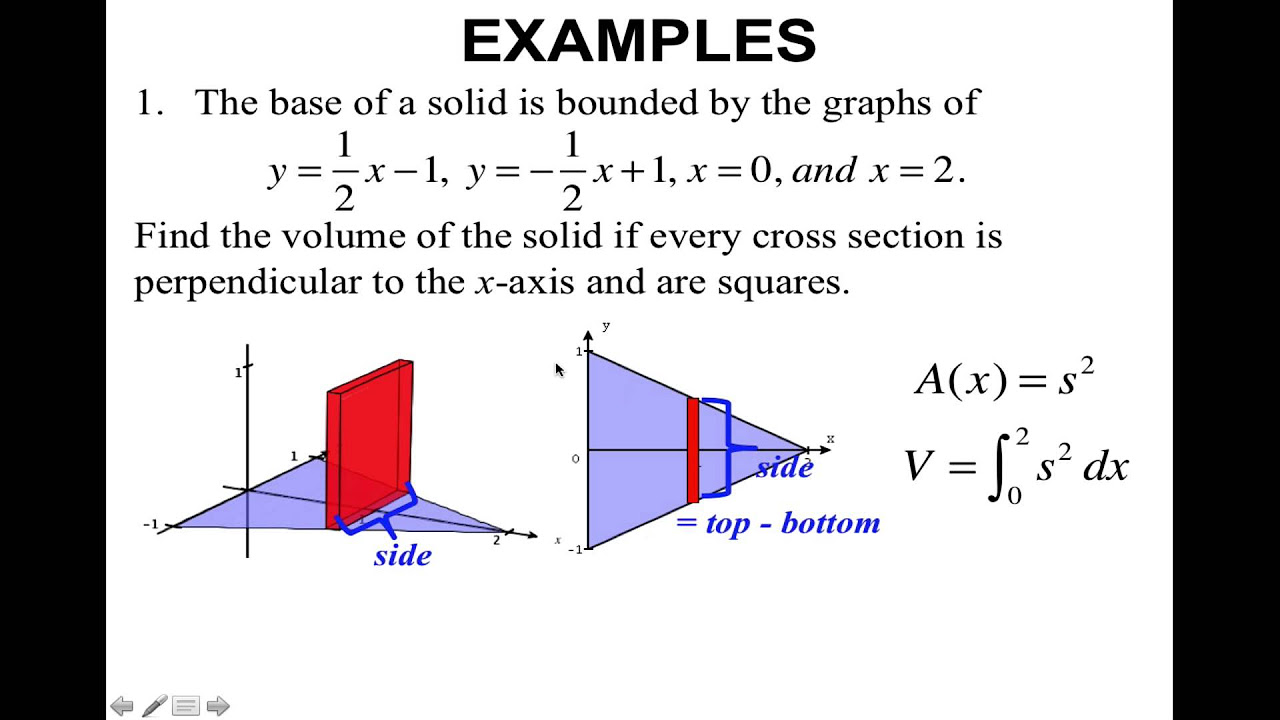
๐Ÿ“ Volume of Solids with Specific Cross-Sections

The second paragraph delves into calculating the volume of a solid whose base is a circle and whose cross sections are perpendicular to the x-axis. The speaker illustrates how to determine the segment (s) for the cross section, which in this case is twice the value of the radical expression 1 - x squared. The integral to find the volume is then set up for squares, semicircles, and equilateral triangles, with the speaker noting that the integrals are straightforward once the segment is identified. The speaker also mentions that the volume calculations often result in relatively small volumes, which might seem counterintuitive given the concept of volume. The key takeaway is that being able to draw the region and knowing the segment allows for easy calculation of volume, with the formulas for the areas of the cross sections being crucial for the integration process.

Mindmap
Keywords
๐Ÿ’กVolume
Volume refers to the amount of space occupied by an object or substance. In the context of the video, it is a key concept as the speaker discusses methods to calculate the volume of different shapes using calculus. The video focuses on integrating the area of cross-sections to find the volume, which is central to the theme of the video.
๐Ÿ’กCalculus
Calculus is a branch of mathematics that deals with rates of change and accumulation of quantities. In the video, calculus is used to find the volume of objects by integrating the areas of their cross-sections. It is the mathematical tool that allows the calculation of volume in the discussed scenarios, making it a fundamental concept in the video.
๐Ÿ’กCross-sections
Cross-sections are the slices taken through an object to analyze its internal structure or shape. In the video, the speaker explains how to calculate volume by considering the area of these cross-sections. The method of finding volume using cross-sections is a primary focus, with the speaker providing formulas for various shapes of cross-sections.
๐Ÿ’กIntegration
Integration is a mathematical operation, the reverse of differentiation, and is used to find the accumulated sum of a series of values. In the video, integration is the process used to calculate the volume of an object by summing up the areas of its cross-sections from one point to another. It is a crucial step in the volume calculation process discussed.
๐Ÿ’กSquare
A square is a geometric shape with four equal sides and four right angles. In the video, the speaker mentions squares as one of the common cross-section shapes for which the volume calculation formula is derived. The area of a square cross-section is s^2, where s is the side length, and it is used as an example to illustrate the volume calculation process.
๐Ÿ’กRectangle
A rectangle is a quadrilateral with four right angles. The video discusses the volume calculation for objects with rectangular cross-sections, emphasizing that the relationship between the base and height (k times the base) must be known. The general formula for the area of a rectangle in terms of s (segment length) is k times s squared.
๐Ÿ’กEquilateral Triangle
An equilateral triangle is a triangle with all three sides of equal length. The video provides a specific formula for the area of an equilateral triangle cross-section in terms of s, which is s squared times the square root of 3 divided by 4. This shape is one of the examples used to demonstrate the volume calculation using cross-sections.
๐Ÿ’กSemicircle
A semicircle is half of a circle. The video explains that the area of a semicircle cross-section in terms of s (the diameter) is pi over 8 times s squared. The semicircle is highlighted as a shape for which the formula should be memorized due to its frequent use in volume calculations.
๐Ÿ’กSegment (s)
In the context of the video, a segment (referred to as 's') is the length between two points on an axis, typically used to define the dimensions of a cross-section. The speaker uses 's' to represent the segment between the upper and lower bounds of a cross-section when calculating volume, which is essential for applying the correct formula for each shape.
๐Ÿ’กScale Factor (k)
The scale factor 'k' is a multiplier used to relate the dimensions of a shape, such as the height to the base in a rectangle. In the video, 'k' is introduced when discussing rectangles, where the height is some multiple of the base (k times the base). Knowing the scale factor is crucial for determining the area of the cross-section and, subsequently, the volume.
๐Ÿ’กMemorization
Memorization is the act of committing information to memory. The video emphasizes the importance of memorizing certain formulas for calculating the areas of cross-sections, such as those for squares, rectangles, equilateral triangles, and semicircles. Memorization is presented as a key strategy for solving volume calculation problems efficiently.
Highlights

Discussed two methods of calculating volume: plane slicing and known cross sections.

Emphasized the importance of expressing the area of a cross-section in terms of the variable of integration (x or y).

Mentioned that squares are the most common cross-section shape but other shapes were also discussed.

Introduced the concept of 's' as a segment within the cross-section for integration purposes.

Provided formulas for the area of different cross-section shapes: square, rectangle, equilateral triangle, and semicircle.

Highlighted the necessity to memorize the area formula for a semicircle as ฯ€/8 * s^2.

Explained the process of calculating the volume of a solid with a circular base and cross sections perpendicular to the x-axis.

Demonstrated the calculation of volume using the integral from -1 to 1 of the cross-sectional area squared.

Noted that for most of these problems, the volume calculated tends to be small.

Stressed that the key to solving these problems is being able to draw the region and determine 's'.

Gave examples of how to find the scale factor for different cross-sectional shapes to calculate volume.

Reassured that these types of problems are straightforward once the cross-sectional area is known.

Suggested that if 's' is not immediately clear, one should redraw the picture and reconsider.

Provided a step-by-step walkthrough for calculating the volume of a solid with square, semicircle, and equilateral triangle cross sections.

Used a calculator to find the volume for the given examples, although it was noted it's not always necessary.

Encouraged memorization of formulas for efficiency in solving similar problems.

Ended the session with a reminder of the importance of understanding the cross-sectional area in terms of the integration variable.

Transcripts

Browse More Related Video

Calculus Integrals for Volumes with Known Cross Sections

Volume Using Known Cross Sections (Slicing) | Calculus 2 Lesson 5 - JK Math

Topic 43-Volumes of Solids with Known Cross Sections

Calculating volume by known cross sections

Calculus AB/BC โ€“ 8.8 Volumes with Cross Sections: Triangles and Semicircles

Calculus 1 Lecture 5.2: Volume of Solids By Disks and Washers Method

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Volume CalculationIntegral CalculusCross-SectionsSquare ShapesRectangle FormulasEquilateral TrianglesSemicircular SectionsMathematical IntegrationGeometry TutorialEducational ContentCalculus Techniques