Calculus Integrals for Volumes with Known Cross Sections

turksvids
21 Apr 201812:43
EducationalLearning
32 Likes 10 Comments

TLDRThis video script delves into the concept of finding volumes with known cross-sections, a less common topic in calculus. It distinguishes between two types of volume problems, focusing on the one where the cross-section is known. The video explains the process of calculating volume by integrating the area function over the bounds, which can be either with respect to x (dx) or y (dy), depending on the orientation of the cross-section. Common cross-sections such as squares, equilateral triangles, semicircles, rectangles, and triangles are discussed, each with its area formula. The script provides a step-by-step approach to solving problems involving these shapes, emphasizing the importance of understanding the geometry and memorizing the area formulas for efficiency. It also covers a unique case where the cross-section's area is given directly as a function of y. The video warns against a common mistake of incorrectly including Ο€ in calculations where it's not needed. The summary aims to clarify the process of finding volumes using cross-sections and encourages viewers to practice these techniques for better understanding and accuracy.

Takeaways
  • πŸš€ The video focuses on the less common calculus problem of finding volumes with known cross-sections, contrasting it with the more common method of revolving a region around an axis.
  • πŸ“š There are two main types of integral setups for volume calculations: πœ‹ times the integral of (big R squared minus little R squared) for horizontal axes, and πœ‹ times the integral of (big R squared minus little R squared) for vertical axes.
  • πŸ”¬ For cross-sectional volume problems, the integral setup changes based on the direction perpendicular to either the x-axis or y-axis, using DX or DY respectively.
  • πŸ“ Key formulas are provided for various cross-sectional shapes like squares (s squared), equilateral triangles (root 3 over 4 times s squared), and semi-circles (πœ‹ over 8 times s squared).
  • πŸ”§ The importance of memorizing area formulas for different cross-sectional shapes to efficiently solve problems is emphasized.
  • πŸ›  Examples illustrate how to determine the function 'S', representing dimensions like the side of a square or the diameter of a semicircle, derived from functions f(x) and g(x).
  • πŸ’Ύ Computational examples are provided, showing how to set up and compute integrals for squares, semicircles, and rectangles, highlighting the necessity of using a calculator for such problems.
  • πŸ“Œ A specific example converting a function from x to y terms is detailed, showcasing how to adjust functions for integrals when the cross-sections are perpendicular to the y-axis.
  • πŸ’‘ The script highlights a common errorβ€”unnecessarily including πœ‹ in volume calculations unless dealing with semicircles, emphasizing understanding over rote memorization.
  • πŸ’ The final message underscores the instructional nature of the video, aiming to aid students in avoiding typical mistakes and enhancing their problem-solving skills in calculus.
Q & A

  • What are the two common types of volume problems in calculus?

    -The two common types of volume problems in calculus are finding the volume when a region is revolved around an axis and finding the volume when the cross-section is known.

  • How do you calculate the volume when revolving a region around a horizontal axis?

    -The volume is calculated using the formula Ο€ times the integral from A to B of (R squared - r squared) dX, where R and r are the outer and inner radii, respectively.

  • What is the formula for calculating the volume when revolving a region around a vertical axis?

    -The volume is calculated using the formula Ο€ times the integral from A to B of (R squared - r squared) dy, where R and r are the outer and inner radii, respectively.

  • What does 'a of X' and 'a of Y' represent in the context of known cross-section volumes?

    -'a of X' and 'a of Y' are functions that give you the area of a cross-section perpendicular to the X-axis and Y-axis, respectively.

  • What is the area formula for a square cross-section?

    -The area formula for a square cross-section is s squared, where 's' is the side length of the square.

  • How do you find the area of an equilateral triangle cross-section?

    -The area of an equilateral triangle cross-section is given by the formula (√3/4) times s squared, where 's' is the side length of the triangle.

  • What is the area formula for a semicircle cross-section?

    -The area formula for a semicircle cross-section is Ο€/8 times s squared, where 's' is the diameter of the semicircle.

  • What is the common mistake made by people when calculating the volume of cross-sections perpendicular to the y-axis?

    -A common mistake is to only use x values for the bounds of integration, instead of y values, which are appropriate for volumes perpendicular to the y-axis.

  • Why is it unnecessary to include Ο€ in the volume calculation unless semicircles are involved?

    -Including Ο€ is unnecessary unless semicircles are involved because the volume calculation does not involve rotation around an axis, which is when Ο€ would be used to account for the circular cross-section.

  • How do you find the area of a rectangle cross-section when the height is three times the base?

    -The area of a rectangle cross-section with a height three times the base is calculated as 3 times s squared, where 's' is the base length of the rectangle.

  • What is the process for finding the area function 's' when the cross-sections are perpendicular to the y-axis?

    -To find 's' when cross-sections are perpendicular to the y-axis, you need to express the right and left boundaries of the region in terms of y, subtract the left boundary from the right to find 's', and then use this in the integral for the volume.

  • What is the easiest way to calculate the volume of a region with cross-sections that are perpendicular to the y-axis and have a given area function?

    -The easiest way is to simply integrate the given area function 'a of Y' from the lower to the upper bounds of the region along the y-axis.

Outlines
00:00
πŸ“š Calculus Volumes with Known Cross-Sections

This paragraph introduces the topic of finding volumes using calculus, focusing on the less common method where the cross-section is known. It explains two primary types of volume problems in calculus: revolving a region around an axis and the direct integration of known cross-sections. The paragraph outlines the process for calculating volume when the cross-section is perpendicular to the x-axis (using dx) or y-axis (using dy), and emphasizes the importance of understanding the area function of the cross-section, which could be in terms of X or Y. It also suggests memorizing formulas for common cross-sections like squares, equilateral triangles, semicircles, and rectangles.

05:01
πŸ“ Working with Cross-Sections Perpendicular to the x-axis

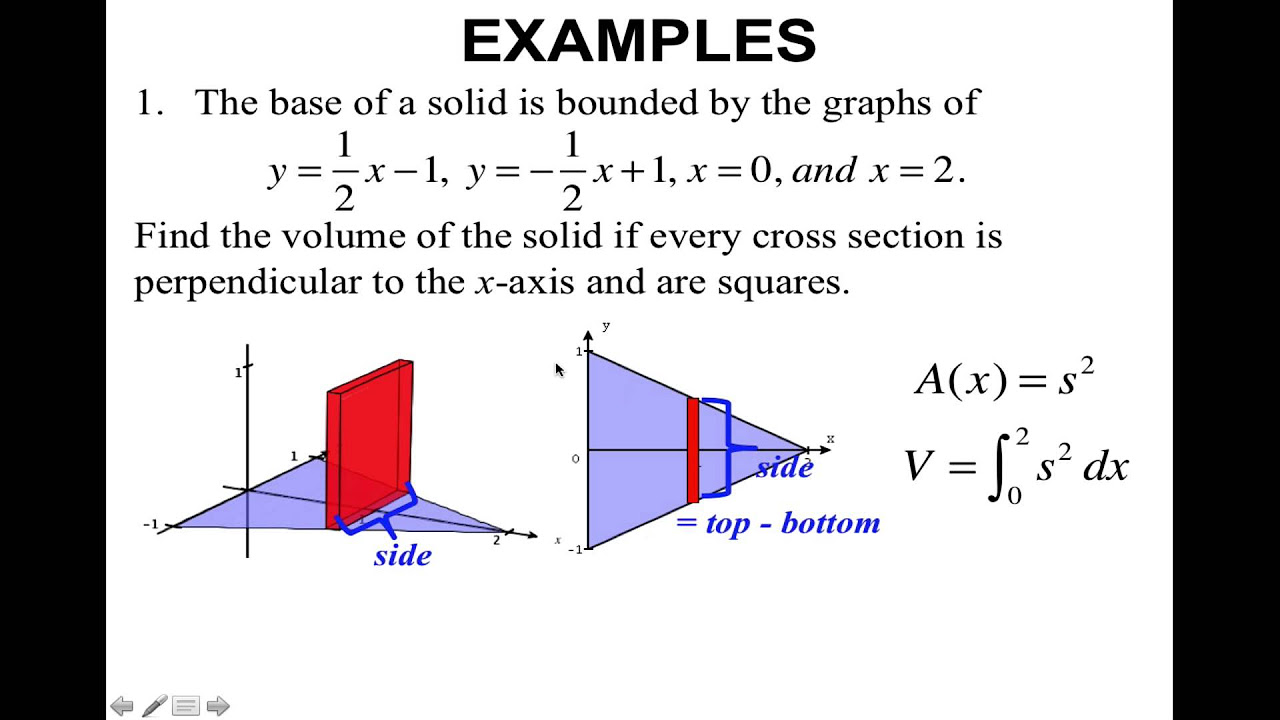
This paragraph delves into the process of calculating volume when the cross-sections are perpendicular to the x-axis. It provides a step-by-step guide for setting up and solving integrals for different types of cross-sections, including squares, semicircles, and rectangles with a height that is a multiple of the base. The paragraph emphasizes the need to identify the correct functions and limits for integration, and it illustrates the process with examples involving squaring the difference between two functions (G(x) - f(x)) and integrating over the interval from A to B. It concludes with the results of using a calculator to find the approximate volumes for each cross-section type.

10:02
πŸ“ˆ Volume Calculations with Cross-Sections Perpendicular to the y-axis

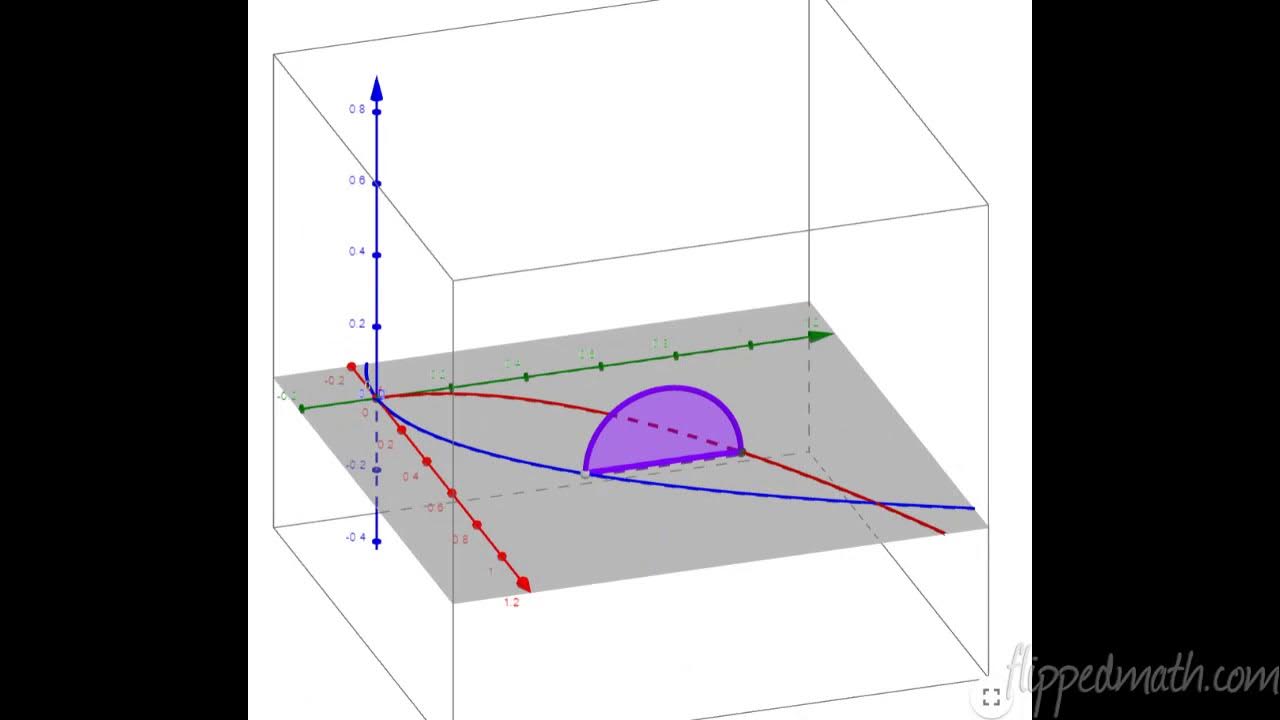
The final paragraph shifts the focus to volume calculations where the cross-sections are perpendicular to the y-axis. It discusses the process of transforming functions from x in terms of y to prepare for dy integration. The paragraph outlines the steps to solve for the variable x when given y, which is essential for setting up the integral. It then presents several problems involving different cross-section shapes, such as squares, isosceles right triangles, and irregular shapes with a specific area function. For each problem, the paragraph details the integration process, highlights common mistakes to avoid, such as incorrectly applying the PI factor, and provides the approximate volume calculated using a calculator. The summary ends with encouragement and well wishes for tackling similar problems.

Mindmap
Keywords
πŸ’‘Volume
Volume in the context of the video refers to the three-dimensional space enclosed by a solid or fluid. It is a fundamental concept in calculus when dealing with problems that involve the rotation of a region around an axis to form a solid. The video discusses methods to calculate volumes of such solids, which is crucial for understanding the material presented.
πŸ’‘Cross-sections
Cross-sections are the two-dimensional slices of a three-dimensional object. In the video, the focus is on finding volumes when the shape of the cross-section is known. Different types of cross-sections, such as squares, equilateral triangles, semicircles, and rectangles, are discussed, each with its own method of calculating the area and subsequently the volume.
πŸ’‘Integration
Integration is a mathematical technique used to calculate the volume of an object by summing up an infinite number of infinitesimally small cross-sectional areas. The video explains how to use integral calculus to find the volume of objects formed by revolving a region around an axis, which is a key method for solving the volume problems discussed.
πŸ’‘Perpendicular to the x-axis
This phrase describes the orientation of the cross-section relative to the x-axis. When the cross-section is perpendicular to the x-axis, the area function is in terms of x, and the bounds for the integral are determined by the y-values. This is a common scenario in the video, where the volume of the solid is calculated by integrating with respect to x (dx).
πŸ’‘Perpendicular to the y-axis
Similar to 'perpendicular to the x-axis', this term describes when the cross-section is perpendicular to the y-axis. In such cases, the area function is in terms of y, and the bounds for the integral are determined by the x-values. The video demonstrates how to handle volume calculations in this orientation, particularly with respect to dy.
πŸ’‘Area function
The area function, denoted as 'a of x' or 'a of y' in the video, is a mathematical function that gives the area of a cross-section at a particular point. It is essential for calculating the volume of the solid formed by revolving the region around an axis. The area function varies depending on the shape of the cross-section and its orientation to the axes.
πŸ’‘Square cross-section
A square cross-section is a type of two-dimensional shape with four equal sides and four right angles. In the video, when the cross-section is a square, the area of the cross-section is calculated as the square of the side length (s^2), where 's' is the distance between the top and bottom curves of the region being revolved.
πŸ’‘Equilateral triangle cross-section
An equilateral triangle cross-section is a shape with three equal sides and three equal angles. The video mentions that the area of such a cross-section can be calculated using the formula (sqrt(3)/4) * s^2, where 's' is the side length, which in this context is the distance between the top and bottom curves of the region.
πŸ’‘Semicircle cross-section
A semicircle cross-section is half of a circle. The video emphasizes the importance of memorizing the area formula for a semicircle, which is PI/8 * s^2, where 's' is the diameter of the semicircle. This shape is significant when calculating volumes involving rotation around an axis.
πŸ’‘Rectangle cross-section
A rectangle cross-section is a quadrilateral with four right angles. The area of a rectangle is calculated as the product of its length and width. In the video, it is mentioned that if the height is a known multiple of the base (e.g., three times the base), the area function can be expressed in terms of 's', the distance between the curves, and the volume is found by integrating this area function.
πŸ’‘Random cross-section
This term refers to a cross-section that does not conform to any standard geometric shape, and its area function 'a of x' or 'a of y' is given directly. The video explains that for such cross-sections, the volume is calculated by integrating the given area function over the bounds determined by the problem. This is the most general case and can encompass a wide variety of shapes.
Highlights

The video discusses finding volumes with known cross-sections, a less common calculus problem.

Two common types of volume problems are those revolving around a horizontal or vertical axis.

For horizontal axis rotation, the volume formula is PI times the integral from A to B of (R^2 - r^2) dx.

For vertical axis rotation, the volume formula is PI times the integral from A to B of (R^2 - r^2) dy.

The video focuses on volume calculation where the cross-section is known and easier to determine.

The integral for volume calculation can be in terms of either x (dx) or y (dy) depending on the axis of rotation.

The area function 'a of x' or 'a of y' is used to determine the area of the cross-section.

Cross-sections can be squares, equilateral triangles, semicircles, rectangles, triangles, or other shapes with specific area formulas.

The area of a square cross-section is s^2, where s is the side length.

The area of an equilateral triangle cross-section is (√3/4)s^2.

The area of a semicircle cross-section is (Ο€/8)s^2, a formula worth memorizing.

For rectangle cross-sections, the area is s times a constant k, often resulting in k*s^2.

The area of a triangle cross-section is 1/2 base times height, requiring knowledge of the relationship between them.

Randomly shaped cross-sections are given by the function 'a of x' or 'a of y', and are the most complex.

The process involves graphing the region, finding intersection points, and using the correct bounds for integration.

An example problem involves the region bounded by f(x) = x^2 - 2x + 1 and g(x) = 4 - e^x, with cross-sections as squares.

The volume of the region with semicircle cross-sections is calculated using the formula PI/8 * ∫(s^2) dx.

For rectangles with height three times the base, the volume is calculated as 3 * ∫(s^2) dx.

When the cross-sections are perpendicular to the y-axis, the integration is done with respect to dy from the bottom to the top y-value of the region.

An example with isosceles right triangle cross-sections shows the integral of (1/2)s^2 from y1 to y2.

A unique case involves cross-sections with an area given by 'a of y', which is integrated directly without additional geometric calculations.

It's important not to incorrectly include PI in the volume calculation unless dealing with semicircles.

The video emphasizes the importance of understanding cross-section shapes and their respective area formulas for volume calculations.

Transcripts

Browse More Related Video

Volumes with Known Cross Sections with Calculus, pg 2

Topic 43-Volumes of Solids with Known Cross Sections

Volume Using Known Cross Sections (Slicing) | Calculus 2 Lesson 5 - JK Math

Calculating volume by known cross sections

Calculus AB/BC – 8.8 Volumes with Cross Sections: Triangles and Semicircles

Calculus AB/BC – 8.7 Volumes with Cross Sections: Squares and Rectangles

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusVolume FindingIntegral TechniquesCross-SectionsMathematical GeometryRevolving ShapesHorizontal AxisVertical AxisSquare Cross-SectionSemicircle Cross-SectionEducational ContentMath TutorialProblem Solving