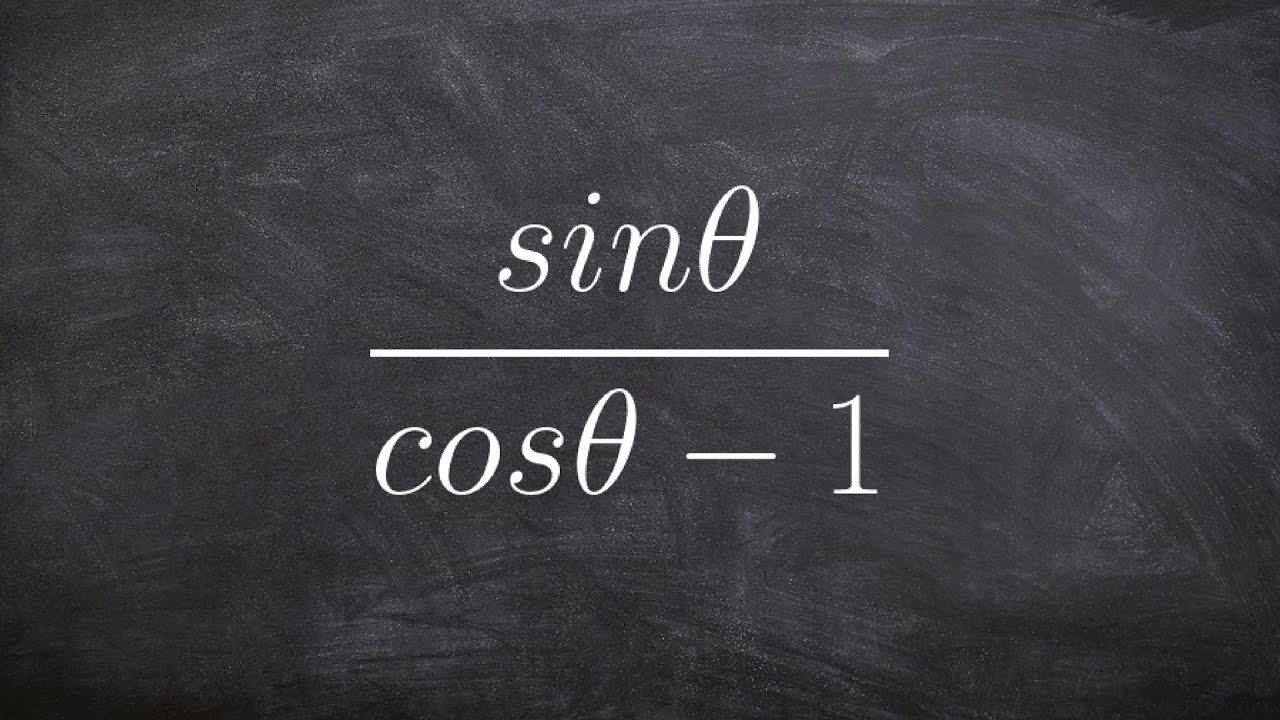Precalc 5.1 Using Fundamental Trig Identities
TLDRThis video tutorial covers the use of fundamental trigonometric identities to simplify expressions. It introduces quotient, reciprocal, and Pythagorean identities, demonstrating how to substitute and manipulate them in various trigonometric expressions. The lesson also explores adding and subtracting trig expressions by finding common denominators and further simplifying them, turning complex problems into simpler trigonometric functions.
Takeaways
- 📚 The video covers the use of fundamental trigonometric identities to simplify expressions.
- 🔍 Quotient identities are introduced, stating that tangent of theta equals sine over cosine, and the reciprocal functions are defined.
- 📐 Pythagorean identities are highlighted, showing the relationships between sine squared, cosine squared, and their sum or difference.
- 🧩 Simplifying trigonometric expressions involves substituting identities to reduce the expression to a simpler form.
- 📉 The example of simplifying sine of X involves using the quotient identity to replace cosecant with cosine over sine.
- 🔄 The concept of factoring is used in the example with sine squared X plus cosine squared X, utilizing the Pythagorean identity.
- 🔢 The video demonstrates solving for a single trigonometric function by manipulating equations and identities.
- 📌 The script mentions that there can be multiple correct answers when simplifying trigonometric expressions, emphasizing the importance of understanding the process.
- 🔗 The process of adding and subtracting trigonometric expressions is compared to adding and subtracting fractions, requiring a common denominator.
- 🔄 The video shows how to combine fractions by finding a common denominator and simplifying the resulting expression.
- 📚 The final takeaway is that simplifying trigonometric functions can be seen as solving trigonometric puzzles, where substitutions and manipulations lead to a simpler form.
Q & A
What are the fundamental trigonometric identities discussed in the video?
-The video discusses the quotient identities, reciprocal identities, and the Pythagorean identities. Specifically, tangent of theta equals sine of theta over cosine of theta, cosecant is 1/sine, secant is 1/cosine, and cotangent is 1/tangent. The Pythagorean identities state that sine squared plus cosine squared equals 1, 1 plus tangent squared equals secant squared, and cosine squared plus 1 equals cotangent squared.
How can the fundamental trigonometric identities be used to simplify expressions?
-The fundamental trigonometric identities can be used to substitute and simplify expressions by replacing complex trigonometric expressions with simpler forms or single trigonometric functions, thus making the expressions easier to work with.
What is the process of simplifying the expression sin(x) * cosec(x) using the identities?
-The process involves recognizing that cosec(x) is the reciprocal of sin(x). By substituting cosec(x) with 1/sin(x), the expression becomes sin(x) * (cos(x) / sin(x)), which simplifies to cos(x), as sin(x) cancels out.
How does the video approach simplifying the expression sin^2(x) + cos^2(x) * sin(2x)?
-The video uses the Pythagorean identity sin^2(x) + cos^2(x) = 1 to simplify the expression to 1 * sin(2x), which is sin(2x).
What is the difference of squares technique mentioned in the video?
-The difference of squares technique is a method used to factor expressions that are in the form of a^2 - b^2, which can be factored into (a + b)(a - b). In the video, it is used to simplify expressions involving trigonometric functions.
How does the video simplify the expression cos(4x) - sin(4x)?
-The video uses the Pythagorean identity to simplify cos^2(x) + sin^2(x) to 1, and then multiplies it by sin(2x) and cos(2x) to get the original expression. After simplification, it results in sin(2x) and cos(2x).
What is the term used by the video to describe the process of simplifying trigonometric expressions using identities?
-The video refers to the process as 'trig puzzles', emphasizing the problem-solving aspect of substituting and simplifying trigonometric expressions.
How does the video handle the expression sin(x) * sec^2(x) - sin^2(x)?
-The video factors out sin^2(x) from both terms, resulting in sin^2(x) * (sec^2(x) - 1). It then uses the identity sec^2(x) = tan^2(x) + 1 to replace sec^2(x) - 1 with tan^2(x), leading to the simplified expression sin(x) * tan^2(x).
What is the common denominator approach used for adding and subtracting trigonometric expressions?
-The common denominator approach involves finding a common denominator for the fractions involved in the trigonometric expressions, which allows for the addition or subtraction of the numerators while keeping the denominator the same.
How does the video simplify the expression sin(theta) / (1 + cos(theta)) + cos(theta) / sin(theta)?
-The video multiplies the first fraction by sin(theta) and the second fraction by (1 + cos(theta)) to get a common denominator of sin(theta) * (1 + cos(theta)). After simplifying the numerators, the expression reduces to 1 / sin(theta), which is equivalent to cosecant(theta).
What advice does the video give for knowing when to stop simplifying trigonometric expressions?
-The video suggests that since there can be more than one correct answer, one should simplify the expression for a few steps and then, if no further simplification seems possible, consider the expression complete.
Outlines
📚 Introduction to Fundamental Trig Identities
The video begins with an introduction to using fundamental trigonometric identities for simplifying expressions. The key identities discussed include quotient identities (e.g., tangent as sine over cosine), reciprocal identities (e.g., cosecant as 1 over sine), and Pythagorean identities (e.g., sine squared plus cosine squared equals one). The aim is to use these identities to simplify trigonometric expressions.
🔄 Example of Simplifying Trig Expressions
An example is provided to demonstrate simplifying a trigonometric expression using identities. The process involves substituting identities into the expression and canceling terms to achieve a simplified form. Specifically, sine of X times cotangent of X is simplified to cosine of X. The goal is to reduce the expression to a single trig function or a simplified version of the original expression.
🧮 Factoring and Pythagorean Identities
The video explains factoring expressions using trigonometric identities. For instance, sin^4(x) - cos^4(x) is factored into (sin^2(x) + cos^2(x))(sin^2(x) - cos^2(x)), using the Pythagorean identity sin^2(x) + cos^2(x) = 1. The expression is further simplified by substitution and combining like terms, resulting in a simplified trigonometric function.
🤔 Multiple Approaches to Solutions
It's emphasized that there can be multiple correct answers when simplifying trigonometric expressions. An example (labeled incorrectly as letter C) demonstrates factoring sin^2(x) out of an expression and using the identity sec^2(x) = tan^2(x) + 1 to simplify it. The concept of trig puzzles is introduced, highlighting the importance of substitutions and manipulations in simplifying expressions.
🔍 Example: Factoring and Canceling Terms
A new example simplifies cos(x) - 2 over cos^2(x) - 4 by factoring the denominator as (cos(x) + 2)(cos(x) - 2) and canceling common terms. This leaves the simplified form 1/(cos(x) + 2). The video advises to stop simplifying when further reduction isn't apparent and to circle the result as the final answer.
➕ Adding and Subtracting Trig Expressions
The lesson covers adding and subtracting trigonometric expressions, similar to adding and subtracting fractions. The need for a common denominator is highlighted, and an example is provided where two fractions are combined by multiplying by their respective denominators. The numerator is simplified using trigonometric identities, resulting in a single term.
💡 Simplifying with Trig Identities
The numerator in the example is simplified using the identity sin^2(theta) + cos^2(theta) = 1. This results in the expression 1 + cos(theta) over sin(theta)(1 + cos(theta)), with the (1 + cos(theta)) terms canceling out. The final simplified form is 1/sin(theta), equivalent to cosecant(theta). The video emphasizes the importance of recognizing when to stop simplifying and highlights that multiple solutions can be correct.
🔄 Further Simplification Examples
The video concludes with another example of adding fractions, highlighting the need for a common denominator. The expression is simplified step-by-step, using identities and factoring where possible. The final simplified form is obtained, and the video reiterates that multiple correct answers are possible when simplifying trigonometric expressions.
Mindmap
Keywords
💡Fundamental Trig Identities
💡Quotient Identities
💡Reciprocal Identities
💡Pythagorean Identities
💡Simplify Trigonometric Expressions
💡Substitution
💡Difference of Squares
💡Factoring
💡Common Denominator
💡Canceling Terms
Highlights
Introduction to using fundamental trig identities to simplify expressions.
Quotient identities: tangent of theta equals sine of theta over cosine of theta.
Reciprocal functions: cosecant is 1/sine, secant is 1/cosine, cotangent is 1/tangent.
Pythagorean identities: sine^2(x) + cosine^2(x) = 1, tangent^2(x) + 1 = secant^2(x), cotangent^2(x) + 1 = cosecant^2(x).
Simplifying a trig expression by substitution using fundamental identities.
Example of substituting cotangent with cosine over sine to simplify an expression.
Factoring a difference of squares involving trig functions.
Using Pythagorean identities to simplify expressions, such as replacing sine^2(x) + cosine^2(x) with 1.
Combining like terms after substitution to simplify the expression further.
Recognizing that there can be more than one correct answer depending on the approach.
Factoring common terms in expressions to simplify them.
Example of manipulating the equation sec^2(theta) = tan^2(theta) + 1 to simplify expressions.
Adding and subtracting trig expressions requires a common denominator.
Simplifying fractions by finding common denominators and using trig identities.
Final simplification steps may vary, and multiple valid answers are possible.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: