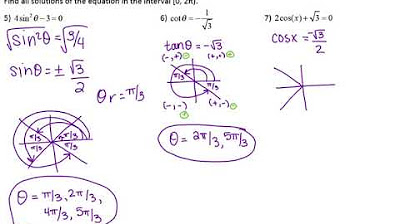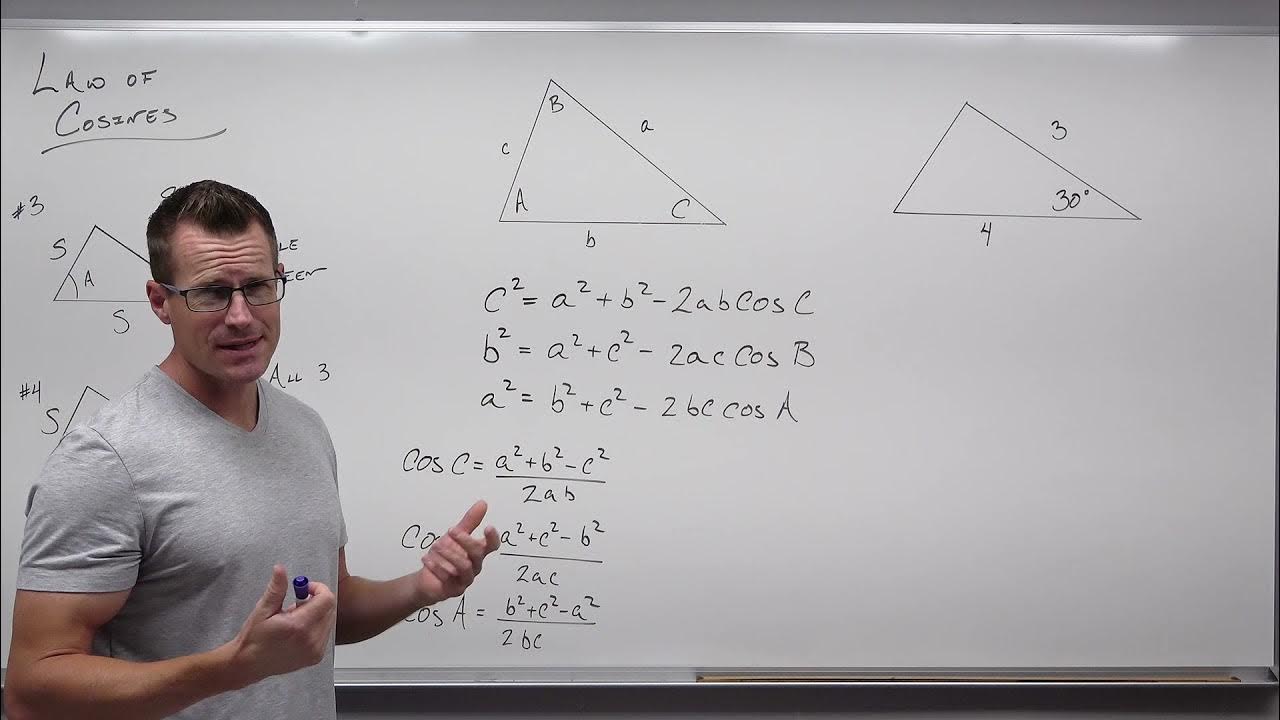Precalculus Chapter 5 test

MathGives YouPower

20 Apr 202246:57

EducationalLearning

32 Likes 10 Comments

TLDRThis video script is a comprehensive review of a pre-calculus chapter 5 test, covering trigonometric identities, solving equations using the law of sines and cosines, and applying Heron's formula. It includes detailed explanations, step-by-step solutions, and graphical representations to aid understanding.

Takeaways

📚 The video is a test review for a Pre-Calculus Chapter 5 test, focusing on trigonometric identities and problems.
📉 Students performed well, but most had at least one problem wrong, indicating the complexity of the problems.
📈 The video covers the use of trigonometric identities such as reciprocal, Pythagorean, and quotient identities to simplify expressions.
🔍 The instructor demonstrates solving problems by factoring, using the Pythagorean identity, and applying the concept of tangent and cotangent.
📐 The video includes practical examples using right triangles to find sine and cosine given the tangent, emphasizing the relationship between these functions.
📝 The process of simplifying complex trigonometric expressions using algebraic manipulation and identities is shown step by step.
📉 The video explains how to find the solutions to trigonometric equations by factoring and using the properties of sine and cosine functions.
📐 The application of the Law of Sines and Cosines is discussed for solving problems related to triangles, including finding unknown sides and angles.
📝 The use of Heron's formula for calculating the area of a triangle when all sides are known is demonstrated, with an emphasis on finding the semi-perimeter first.
🔢 The video provides a method for finding the number of real solutions to a trigonometric equation over a given interval by graphing and analyzing the crossings of the x-axis.
📝 Lastly, the video shows how to use trigonometric identities to produce sine x, connecting it to the concept of cosecant and simplifying the expression.

Q & A

What is the main topic of the video?
-The main topic of the video is a test review for a pre-calculus chapter 5 test, focusing on trigonometric identities and problems.
What are the trigonometric identities used in the video?
-The video discusses reciprocal identities, Pythagorean identities, and quotient identities such as tangent and cotangent.
How is the problem involving sine squared x plus cosine squared x simplified?
-The problem is simplified using the Pythagorean identity that states sine squared x plus cosine squared x equals one.
What is the relationship between tangent theta and sine theta?
-Tangent theta is equal to sine theta divided by cosine theta, and it is positive when cosine theta is greater than zero.
How is the value of sine theta and cosine theta determined when tangent theta is given as five?
-By using the relationship between tangent and sine/cosine, and knowing that tangent theta is the opposite side over the adjacent side in a right triangle, sine theta is found to be 5/√26 and cosine theta is 1/√26.
What is the correct answer for the problem involving secant squared x plus one times secant x minus one?
-The correct answer is D, as the expression simplifies to secant squared x minus one over sine squared x, which further simplifies to 1 over cosine squared x.
How many solutions does the trigonometric equation 2 sine squared x plus sine x equals 1 have over the interval from 0 to 2 pi?
-There are three solutions to the equation over the interval from 0 to 2 pi.
What is the method used to find the distance from meteorologist point B to the tornado in the given scenario?
-The method used is the Law of Sines, which involves finding the unknown side opposite a known angle.
What is the measure of angle C in the triangle where side a is opposite to angle C and the sine of angle C is given?
-Angle C is found using the inverse sine function, specifically the inverse sine of (side opposite angle C / side adjacent to angle C).
How is the area of triangle ABC calculated in the video?
-The area of triangle ABC is calculated using Heron's formula, which involves finding the semi-perimeter and then the square root of the product of the semi-perimeter and the differences of the sides.
What is the reference angle for an angle of 310 degrees?
-The reference angle for an angle of 310 degrees is 50 degrees, found by subtracting the angle from 360 degrees.
How is the distance d between the ship and the island calculated in the video?
-The distance d is calculated using the Law of Sines, where d is equal to the known side (20 miles) times the sine of the known angle (36 degrees) divided by the sine of the angle opposite the known side.
What is the correct answer for the problem involving the distance of segment BC in triangle ABC?
-The correct answer is 16.5, found by using the Law of Sines and calculating the side opposite the known angle.
What is the correct answer for the problem involving the distance of segment FG in triangle EFG?
-The correct answer is 34.6, found by using the Law of Cosines to calculate the unknown side.
How many real solutions does the equation 3 cosine squared x plus cosine x minus two equal zero have over the interval from 0 to 2 pi?
-The equation has three real solutions over the interval from 0 to 2 pi.
What is the final step in solving the equation involving sine squared theta plus cosine squared theta?
-The final step is to recognize that sine squared theta plus cosine squared theta equals 1, and thus the equation simplifies to sine x equals sine x, confirming the identity.

Outlines

00:00

📚 Pre-Calculus Test Review

This paragraph provides an overview of a pre-calculus chapter 5 test review for the 2021-2022 school year. The test included various problems, most of which students solved correctly, with only one problem causing widespread errors. The focus was on simplifying trigonometric identities using standard formulas, including reciprocal, Pythagorean, and quotient identities. The video aims to guide students through solving these problems, starting with a trigonometric identity simplification involving sine and cosine functions.

05:00

🔍 Solving Trigonometric Identity Problems

The paragraph delves into solving a specific trigonometric identity problem, which involves simplifying an expression using the Pythagorean identity. The problem starts with a complex fraction that simplifies to secant squared x minus one, over sine squared x. By applying the Pythagorean identity, the expression is further simplified to sine squared theta over cosine squared theta, which eventually simplifies to secant squared x. The correct answer to the problem is identified as 'd'.

10:02

📐 Applying Trigonometric Equations to a Triangle

This section discusses solving a trigonometric equation over the interval from 0 to 2π. The equation 2 sine squared x plus sine x equals 1 is factored and solved algebraically, revealing solutions at pi/6 and 5π/6. The paragraph also describes a graphical method to solve the equation, demonstrating the use of a graphing calculator to find the solutions, which align with the algebraic method.

15:03

📐 Law of Sines in Triangle Problems

The paragraph explains the application of the Law of Sines to find the measure of side 'a' in a triangle, given the angle opposite to it and another side. The process involves setting up a ratio using the sine of the known angle and the length of the side opposite it, equal to the sine of the given angle and the unknown side. The calculation is performed using a calculator, and the answer is rounded to the nearest tenth.

20:03

🌡️ Meteorologists and the Law of Sines

This section presents a problem involving two meteorologists located 25 miles apart on an east-west road, observing a tornado. Using the Law of Sines, the distance from one meteorologist to the tornado is calculated by finding the complementary angles to the given bearings and then determining the unknown side opposite the calculated angle. The process involves converting the angles to radians and using the sine function to find the unknown distance.

25:05

🚤 Law of Sines for Ship and Island Distance

The paragraph describes a scenario where the distance between a ship and an island is to be found using the Law of Sines. Given the angle and the side opposite it, the calculation involves setting up a ratio with the sine of the angle and the known side, which is then used to find the unknown distance 'd'. The calculation is performed, and the result is rounded to the nearest tenth mile.

30:06

🤔 Evaluating Law of Cosines and Sines Applications

This section involves a problem where the Law of Cosines is to be applied to find an unknown side in a triangle. The paragraph discusses the conditions under which the Law of Cosines is applicable, such as having three known sides or a known side opposite a known angle. It also clarifies that the Law of Sines is not suitable in this case due to the lack of a known angle opposite the side to be found.

35:08

📐 Heron's Formula for Triangle Area

The paragraph explains the process of finding the area of a triangle using Heron's formula. It involves calculating the semi-perimeter of the triangle and then using it in Heron's formula to find the area. The paragraph also discusses a mistake made in a test version and the correct method to find the area, including using a calculator program for Heron's formula.

40:09

📏 Calculating Triangle Sides and Angles

This section covers the process of finding the measure of angle 'c' in a triangle using the Law of Cosines. The calculation involves using the known sides of the triangle and the Law of Cosines formula to find the cosine of the angle, which is then used to determine the angle itself. The result is rounded to the nearest degree.

45:10

🌐 Solving Trigonometric Equations Graphically

The paragraph describes a method for solving trigonometric equations by graphing. It explains how to set up a graphing window for the interval from 0 to 2π and how to graph the equation to find the number of real solutions by counting the times the graph crosses the x-axis.

🔄 Trigonometric Identities to Solve for Sine

The final paragraph discusses the use of trigonometric identities to solve for sine in an equation. It shows how to manipulate the equation using the identity that sine squared theta plus cosine squared theta equals 1, and then solve for sine by recognizing that 1 over cosecant x is equal to sine x.

Mindmap

Keywords

💡Trigonometric Identities

Trigonometric identities are fundamental equations that relate different trigonometric functions of the same angle. In the video, these identities are used to simplify complex expressions, such as converting tangent theta to sine and cosine ratios. The script mentions using reciprocal identities, Pythagorean identities, and quotient identities to solve problems, demonstrating their crucial role in pre-calculus.

💡Pythagorean Identities

Pythagorean identities are a set of trigonometric identities that relate the squares of sine and cosine functions to 1. Specifically, the identity states that sine squared theta plus cosine squared theta equals 1. This identity is used in the script to simplify expressions and solve for unknowns, such as simplifying sine squared x plus cosine squared x to 1 in a given problem.

💡Reciprocal Identities

Reciprocal identities in trigonometry are identities that express one trigonometric function as the reciprocal of another. For example, cotangent theta is the reciprocal of tangent theta, which is cosine theta divided by sine theta. In the script, these identities are used to simplify expressions involving tangent and cotangent, helping to solve trigonometric equations.

💡Tangent

Tangent is a trigonometric function that represents the ratio of the opposite side to the adjacent side in a right-angled triangle. In the video, tangent is used to find sine and cosine values when given the tangent of an angle, as seen when solving for sine theta and cosine theta given tangent theta is five.

💡Sine and Cosine

Sine and cosine are fundamental trigonometric functions that relate the angles of a right triangle to the lengths of its sides. In the script, sine and cosine are used extensively to solve problems involving right triangles, such as finding the lengths of sides when given an angle and its opposite side, or determining angles when given side lengths.

💡Law of Sines

The Law of Sines is a formula used in trigonometry to relate the lengths of sides of a triangle to the sines of its angles. In the video, the Law of Sines is used to find unknown side lengths when a side and its opposite angle are known, as demonstrated in the problem involving triangle ABC.

💡Law of Cosines

The Law of Cosines is another trigonometric formula used to relate the lengths of sides of a triangle to the cosine of one of its angles. In the script, the Law of Cosines is mentioned as a method to solve for unknown sides or angles in triangles, particularly when dealing with non-right triangles.

💡Reference Angle

A reference angle is the acute angle formed by a line and the x-axis in standard position. In the video, the reference angle is used to find the measure of an angle when given an angle greater than 90 degrees, such as finding the reference angle for 310 degrees by subtracting it from 360 degrees.

💡Heron's Formula

Heron's Formula is a method for finding the area of a triangle when the lengths of all three sides are known. In the script, Heron's Formula is used to calculate the area of triangle ABC by first finding the semi-perimeter and then using the formula involving the sides and the semi-perimeter.

💡Trigonometric Equations

Trigonometric equations involve trigonometric functions and are solved using trigonometric identities and methods. In the video, trigonometric equations like 2 sine squared x plus sine x equals 1 are solved using factoring and applying trigonometric identities, demonstrating the application of these equations in pre-calculus.

💡Complementary Angles

Complementary angles are two angles whose sum is 90 degrees. In the script, complementary angles are used to find the measure of an angle when given the measure of its complement, such as finding the complementary angle to 38 degrees by subtracting it from 90 degrees.

Highlights

Introduction to a test review video for a pre-calculus chapter on trigonometric identities.

Students performed well, with most getting at least one problem wrong, indicating the test's challenging nature.

Emphasis on using basic trigonometric identities for simplification, including reciprocal and Pythagorean identities.

Demonstration of factoring out common factors like sine x from trigonometric expressions.

Explanation of how to use the Pythagorean identity to simplify sine squared x + cosine squared x to 1.

Approach to finding sine and cosine values given the tangent of an angle and its sign.

Graphical representation to determine the values of sine and cosine from a right triangle.

Simplification of a complex trigonometric expression using secant and tangent identities.

Use of the identity 1 + tangent squared theta = secant squared theta to simplify expressions.

Solving trigonometric equations by factoring and applying algebraic methods.

Finding solutions to the equation 2 sine squared x + sine x = 1 by factoring and using unit circle references.

Application of the Law of Sines to find the measure of side a in a triangle with known angle and side.

Using the Law of Sines to find the measure of angle c in a triangle with known sides and angles.

Solving for the distance from a meteorologist to a tornado using complementary angles and the Law of Sines.

Distinguishing between the Law of Sines and the Law of Cosines based on the given information in a triangle.

Calculating the distance between a ship and an island using the Law of Sines with given angles and sides.

Determining the correct application of trigonometric laws in various triangle problems.

Finding the area of a triangle using Heron's formula and the semi-perimeter.

Using the Law of Cosines to find the measure of angle c in a triangle with known sides.

Solving for the distance of a segment in a triangle using the Law of Sines with a known angle and side.

Calculating the area of a triangle using Heron's formula with programmed calculator functions.

Determining the number of real solutions to a trigonometric equation within a given interval.

Using trigonometric identities to produce sine x and verifying the identity.

Transcripts

Browse More Related Video

Precalc Chapter 5 Review

Trig Identities

How to Use the Law of Cosines in Trigonometry (Precalculus - Trigonometry 33)

How to Prove Trigonometric Identities (Precalculus - Trigonometry 24)

PreCalculus Midterm Exam Review

Introduction to Using Trigonometric Identities (Precalculus - Trigonometry 23)

Related Tags

Trigonometry Review Pre-Calculus Test Strategies Math Education Pythagorean Identities Trigonometric Problems Sine and Cosine Law of Sines Law of Cosines Heron's Formula