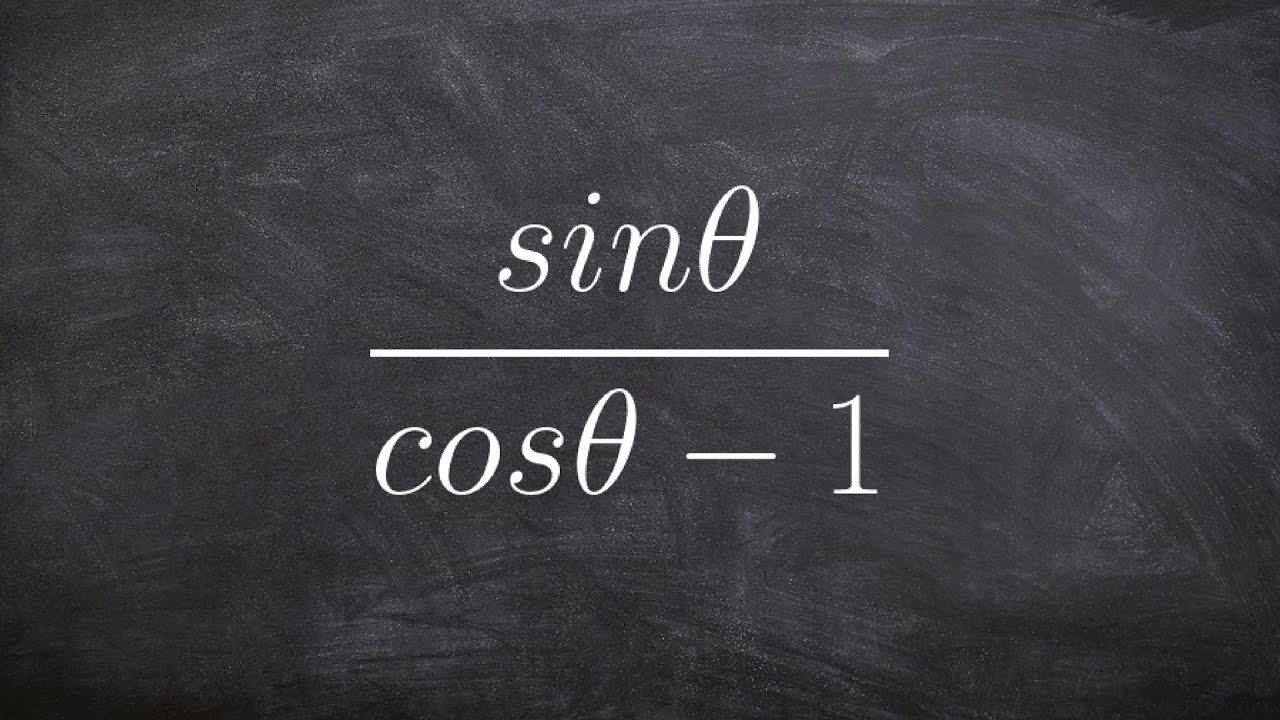5.1.5 Simplifying Trigonometric Expressions

Justin Backeberg
29 Feb 202007:36
EducationalLearning
32 Likes 10 Comments

TLDRIn this video, Mr. Banker teaches viewers how to simplify complex trigonometric expressions using algebraic techniques and trigonometric identities. He demonstrates how to factor out common terms, apply the Pythagorean identity, and use quotient identities to transform complicated expressions into simpler forms, making them more manageable for higher-level math and calculus.

Takeaways
  • 📚 The video focuses on simplifying trigonometric expressions, which is essential for higher-level math classes like calculus.
  • 🔍 The first example shows simplifying the expression (sin^3(x) + sin(x)cos^2(x)) by factoring out (sin(x)) as a common factor.
  • 🧩 After factoring, the expression is simplified using the Pythagorean identity (sin^2(x) + cos^2(x) = 1), resulting in just (sin(x)).
  • 📈 The second example involves expanding and simplifying the expression (sec(x) + 1) * (sec(x) - 1) using the FOIL method for multiplication.
  • 🔄 The expression is simplified by recognizing that (sec^2(x) - 1) is equivalent to (tan^2(x)), and then further simplified to (sec^2(x)).
  • 🌐 The third example deals with combining fractions and simplifying them using common denominators and trigonometric identities.
  • 🔢 The fractions (cos(x)/(1 - sin(x))) and (-sin(x)/cos(x)) are combined by finding a common denominator, (cos(x)(1 - sin(x))).
  • 🔄 The numerator is rearranged to show the Pythagorean identity, simplifying the expression to (sec(x)).
  • 📉 The video emphasizes the importance of using trigonometric identities and algebraic techniques to simplify complex trigonometric expressions.
  • 📘 The process involves factoring, expanding, using Pythagorean identities, and combining fractions with common denominators to achieve simplification.
Q & A

  • What is the main focus of the video by Mr. Banker?

    -The main focus of the video is to simplify trigonometric expressions, which are often encountered in higher-level math classes and specifically in calculus.

  • What is the first trigonometric expression Mr. Banker simplifies in the video?

    -The first expression is sine cubed of X plus the sine of X times the cosine squared of X, which is simplified by factoring out the sine of X and using the Pythagorean identity.

  • What algebraic technique does Mr. Banker use to simplify the first expression?

    -Mr. Banker uses the technique of factoring out the greatest common factor (GCF), which in this case is the sine of X.

  • What Pythagorean identity is used in the first example to simplify the expression?

    -The identity used is sine squared of X plus cosine squared of X equals one, which simplifies the expression to just the sine of X.

  • What is the second example in the video about?

    -The second example involves expanding and simplifying a fraction that includes secant of X terms, using the Pythagorean identity and quotient identity.

  • How does Mr. Banker expand the expression involving secant of X in the second example?

    -He uses the FOIL method (First, Outer, Inner, Last) to expand the expression (secant of X + 1) * (secant of X - 1).

  • What identity does Mr. Banker replace secant squared of X minus 1 with in the second example?

    -He replaces secant squared of X minus 1 with tangent squared of X, using the Pythagorean identity.

  • What is the result of simplifying the second example in the video?

    -The result of simplifying the second example is secant squared of X, after using identities and canceling terms.

  • What is the third example in the video about?

    -The third example involves combining fractions and simplifying an expression with cosine and sine terms, using common denominators and Pythagorean identities.

  • How does Mr. Banker find a common denominator for the fractions in the third example?

    -He multiplies each fraction by the denominator of the other fraction to achieve common denominators of cosine of X times (1 - sine of X).

  • What is the final simplified form of the third example in the video?

    -The final simplified form is secant of X, after canceling out terms and using the Pythagorean identity.

Outlines
00:00
📚 Simplifying Trigonometric Expressions in Higher-Level Math

This paragraph introduces the topic of simplifying trigonometric expressions, particularly in the context of higher-level math classes like calculus. The speaker, Mr. Banker, aims to demonstrate how to simplify complex trigonometric equations and expressions using identities and algebraic techniques. The first example involves simplifying an expression with sine cubed and sine times cosine squared, by factoring out the common sine of X and applying the Pythagorean identity to reduce the expression to just sine of X. The focus is on making the process of dealing with trigonometric expressions more manageable.

05:00
🔍 Expanding and Simplifying Trigonometric Fractions Using Identities

The second paragraph delves into the process of expanding and simplifying a trigonometric fraction involving secant of X. The speaker explains the use of the distributive property (FOIL method) to expand the expression and then cancels terms to simplify it. The key step involves recognizing the Pythagorean identity that secant squared of X minus 1 is equivalent to tangent squared of X. The speaker then uses the quotient identity to express tangent squared in terms of sine and cosine, leading to the final simplified form of secant squared of X. The paragraph illustrates the power of trigonometric identities in simplifying complex expressions.

Mindmap
Keywords
💡Trigonometric expressions
Trigonometric expressions involve functions like sine, cosine, and tangent, which are used to describe the relationships between the angles and sides of triangles, particularly right triangles. In the video, the focus is on simplifying these expressions, which is crucial for solving complex mathematical problems in higher-level math classes like calculus. The script mentions simplifying expressions like sine cubed of X plus sine of X times cosine squared of X.
💡Simplification
Simplification in mathematics refers to the process of making an equation or expression easier to understand or work with by reducing it to its simplest form. In the context of the video, simplification involves using trigonometric identities and algebraic techniques to reduce complex trigonometric expressions into simpler forms, making them more manageable for further calculations or analysis.
💡Pythagorean identity
The Pythagorean identity is a fundamental trigonometric identity that states that the square of sine plus the square of cosine of the same angle is equal to one: \(\sin^2(x) + \cos^2(x) = 1\). This identity is used in the video to simplify expressions by replacing the sum of sine squared and cosine squared with the number one, as seen when simplifying the expression involving sine cubed of X.
💡Factoring
Factoring is an algebraic technique used to break down a polynomial or expression into a product of its factors. In the video, factoring is used to simplify trigonometric expressions by identifying common factors, such as sine of X, and pulling them out as a common factor, which helps in reducing the complexity of the expression.
💡Secant
Secant is a trigonometric function defined as the reciprocal of the cosine function: \(\sec(x) = \frac{1}{\cos(x)}\). In the video, secant is used in expressions and is manipulated using trigonometric identities to simplify them. For example, the script discusses simplifying an expression involving secant squared of X minus 1, which is related to the tangent squared of X.
💡Tangent
Tangent is a trigonometric function defined as the ratio of the opposite side to the adjacent side in a right triangle, or in terms of sine and cosine, \(\tan(x) = \frac{\sin(x)}{\cos(x)}\). The video uses the tangent function in its squared form to simplify expressions, demonstrating how tangent squared can be expressed as sine squared over cosine squared.
💡Quotient identity
A quotient identity in trigonometry is an identity that relates the quotient of two trigonometric functions to another trigonometric function. In the video, the quotient identity for tangent is used to express tangent squared as sine squared over cosine squared, which helps in simplifying the given trigonometric expression.
💡FOIL
FOIL is a mnemonic used to remember the steps for multiplying two binomials: First, Outer, Inner, Last. In the video, FOIL is used to expand the product of two binomials, such as secant of X plus 1 times secant of X minus 1, which results in secant squared of X minus 1.
💡Common denominators
A common denominator is a single denominator that is shared by multiple fractions, allowing them to be added or subtracted. In the video, the script discusses finding common denominators for fractions involving cosine of X and sine of X, which is necessary for combining them into a single fraction.
💡Commutative property
The commutative property of addition states that the order in which two numbers are added does not change the sum. In the video, this property is used to rearrange terms in the numerator of a fraction to make it easier to identify and apply trigonometric identities, such as the Pythagorean identity.
💡Secant squared
Secant squared is the square of the secant function, which is the reciprocal of the cosine function squared: \(\sec^2(x) = \left(\frac{1}{\cos(x)}\right)^2\). In the video, secant squared is used in the simplification process, ultimately being reduced to a simpler form through the application of trigonometric identities and algebraic manipulation.
Highlights

Introduction to simplifying trigonometric expressions in higher-level math classes like calculus.

Goal is to simplify complex trigonometric expressions for easier manipulation.

First example involves simplifying sine cubed of X plus sine of X times cosine squared of X.

Factoring out sine of X as a common factor in both terms.

Using the Pythagorean identity sine squared of X plus cosine squared of X equals one.

Simplifying the expression to just sine of X.

Second example involves expanding and simplifying secant of X plus 1 times secant of X minus 1.

Applying the FOIL method to multiply out the terms.

Canceling terms to simplify the expression to secant squared of X minus 1 over sine squared of X.

Using the Pythagorean identity to replace secant squared of X minus 1 with tangent squared of X.

Simplifying further by separating the numerator and using the quotient identity for tangent squared.

Canceling out sine squared terms to end up with secant squared of X.

Third example focuses on combining fractions involving cosine of X over 1 minus sine of X and sine of X over cosine of X.

Achieving common denominators by multiplying each fraction by the other's denominator.

Rearranging terms in the numerator to utilize the Pythagorean identity.

Simplifying the expression to secant of X.

Final simplified result is secant squared of X.

Transcripts

Browse More Related Video

How do you simplify trigonometric expressions

Precalc 5.1 Using Fundamental Trig Identities

Precalc 5.2 Verifying Trig Identities

Simplifying Trigonometric Expressions

Ex 2: Simplify Trigonometric Expressions

5.2.1 Proving Trigonometric Identities

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
TrigonometryCalculusSimplificationMathematicsEducationalTutorialPythagorean IdentitiesAlgebraic TechniquesFactoringTrig Identities