5.2.1 Proving Trigonometric Identities

Justin Backeberg

3 Mar 202014:40

EducationalLearning

32 Likes 10 Comments

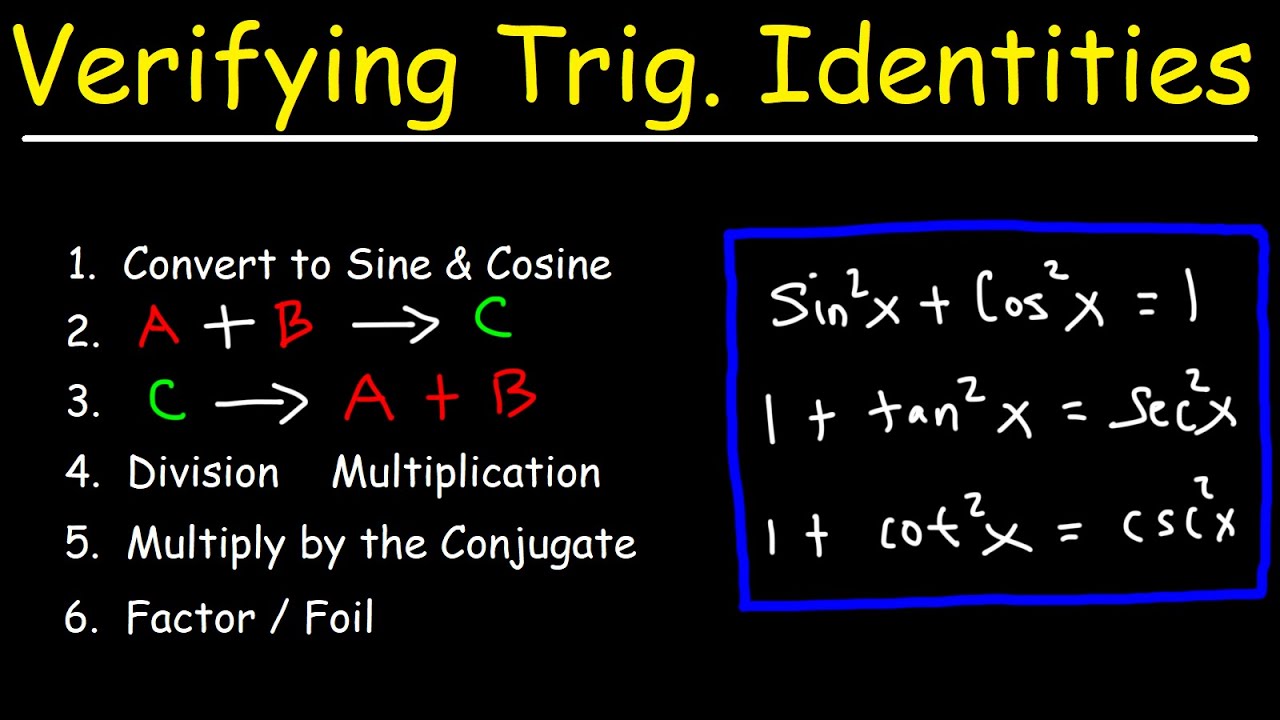
TLDRIn this educational video, Mr. Banker guides viewers through the process of proving trigonometric identities. He emphasizes the importance of working with one side of the equation at a time, finding common denominators, factoring, and using trigonometric identities to simplify expressions. The video demonstrates several examples, showcasing strategies like converting everything into sines and cosines and switching sides when stuck, ultimately proving the identities.

Takeaways

📚 The video focuses on proving trigonometric identities by transforming one expression into another through algebraic manipulations and trigonometric identities.
🔍 It's recommended to work with one side of the equation at a time, starting with the more complicated side and working towards the simpler side.
📉 Helpful hint number one suggests that working with the more complex side first can simplify the process of proving identities.
📚 Factoring, adding fractions, and simplifying expressions are key strategies in proving identities, as mentioned in helpful hint number two.
🔄 Helpful hint number three emphasizes the importance of using fundamental trigonometric identities to replace functions in the expressions.
🔄 If stuck, converting everything into sines and cosines can provide a clearer path towards proving the identity.
🔄 Switching sides if one side becomes too complex is a valid strategy to find a common middle point between the two sides of the equation.
📈 The first example demonstrates proving the identity that the tangent of X plus the cotangent of X equals the secant of X times the cosecant of X.
📉 The second example shows how to prove the identity involving 1 over the secant of X, focusing on finding common denominators and simplifying fractions.
📊 The third example involves proving an identity with cosine and sine, highlighting the use of Pythagorean identities and the distributive property.
📚 The final example demonstrates proving an identity involving cotangent, secant, and tangent, showcasing the use of Pythagorean identities and the commutative property of addition.

Q & A

What is the main goal when proving identities?
-The main goal when proving identities is to show that two given expressions are equal by transforming one side of the equation into the other through algebraic manipulations and trigonometric identities.
Why is it often better to start with the more complicated side of the equation?
-It's often better to start with the more complicated side of the equation because it provides more opportunities for simplification and substitution, making it easier to transform into the simpler side.
What should you do if you get stuck on one side of the equation?
-If you get stuck on one side of the equation, you can try switching to the other side and look for a common middle point between the two sides.
What is a helpful hint for working with fractions in trigonometric identities?
-A helpful hint for working with fractions is to look for opportunities to factor, add fractions, square binomials, or get a monomial denominator if dealing with fractions.
How can converting everything into sines and cosines help in proving identities?
-Converting everything into sines and cosines can help in finding a path to the solution because it simplifies the expressions and makes it easier to apply fundamental trigonometric identities.
What is the first step in the example where tangent of X plus cotangent of X is equal to secant of X times cosecant of X?
-The first step is to convert the tangent and cotangent into sines and cosines using their quotient identities.
What identity is used to simplify the numerator in the example involving tangent of X plus cotangent of X?
-The Pythagorean identity, which states that sine squared of X plus cosine squared of X equals 1, is used to simplify the numerator.
Why might it be beneficial to split a large fraction into two smaller fractions?
-Splitting a large fraction into two smaller fractions can make it easier to recognize and apply reciprocal identities.
In the second example, how are the common denominators found for the fractions involving secant of X?
-The common denominators are found by multiplying the numerator and denominator of each fraction by the opposite fraction's denominator.
What strategy is suggested if it's not obvious what to do next when proving an identity?
-If it's not obvious what to do next, a suggested strategy is to convert everything into sines and cosines to simplify the expressions.

Outlines

00:00

📚 Introduction to Proving Identities

In this video, Mr. Banker introduces the concept of proving identities in trigonometry. The goal is to demonstrate that two given expressions are equal by transforming one side of the equation into the other through algebraic manipulations and trigonometric identities. Helpful hints are provided to guide the process, such as working with one side of the equation at a time, factoring, adding fractions, and using fundamental trigonometric identities. The video emphasizes the importance of attempting solutions even if they lead to a dead end, as this is better than not trying at all.

05:03

🔍 Proving Tangent Plus Cotangent Equals Secant Times Cosecant

The first example in the video involves proving that the sum of tangent and cotangent of an angle X is equal to the product of secant and cosecant of X. Mr. Banker suggests starting with the more complex side, which in this case is the left side of the equation. He converts tangent and cotangent into sine and cosine using quotient identities, then finds a common denominator to combine the fractions. Utilizing the Pythagorean identity, he simplifies the expression to match the right side of the equation, thus completing the proof.

10:05

🔄 Simplifying Expressions Involving Secant and Cosecant

The second example demonstrates how to simplify an expression involving secant and cosecant. Mr. Banker starts by finding a common denominator for the fractions on the left side of the equation. After simplifying the numerators and denominators using algebraic identities, he ends up with an expression that matches the right side of the equation. This example shows the importance of manipulating fractions and using trigonometric identities to simplify complex expressions.

📉 Proving Identities Involving Cosine and Sine

In the third example, Mr. Banker tackles an identity involving cosine and sine. He starts by manipulating the right side of the equation, multiplying by cosine to simplify the expression. Using Pythagorean identities, he transforms the equation into a form that matches the left side. This example highlights the strategy of converting trigonometric functions into sines and cosines to find a path to the solution.

🔄 Advanced Identity Proof: Cotangent Squared Over Cosecant Equals Cotangent Times Secant Minus Tangent

The final example in the video involves proving a complex identity involving cotangent, secant, and tangent. Mr. Banker begins by simplifying the left side of the equation using Pythagorean identities and factoring. He then switches to the right side, converting trigonometric functions into sines and cosines, and applying distributive properties to match the left side. This example illustrates the technique of switching sides and finding a common middle point to prove an identity.

Mindmap

Keywords

💡Proving Identities

Proving identities in mathematics involves demonstrating that two expressions are equivalent. In the context of the video, this process is central to the theme as the presenter guides viewers through the steps of transforming one expression into another using algebraic manipulations and trigonometric identities. The goal is to show that the initial expressions are indeed equal, which is a fundamental concept in trigonometry.

💡Algebraic Manipulations

Algebraic manipulations refer to the mathematical techniques used to rearrange and simplify expressions. In the video, these manipulations are crucial for transforming one side of an equation into the form of the other side. Examples include combining fractions, factoring, and using identities to simplify expressions, which are all demonstrated in the script.

💡Trigonometric Identities

Trigonometric identities are equations that hold true for all values of the variables for which both sides of the equation are defined. The video discusses using these identities, such as Pythagorean identities and quotient identities, to prove the equality of different trigonometric expressions. These identities are foundational in the process of proving identities.

💡Tangent

The tangent function, often abbreviated as 'tan', is a trigonometric function that relates the ratio of the opposite side to the adjacent side in a right triangle. In the video, tangent is used in the context of proving identities, such as in the expression 'tan(x) + cot(x)', where 'cot' is the cotangent, the reciprocal of the tangent.

💡Cotangent

Cotangent, denoted as 'cot', is the reciprocal of the tangent function. It is used in the video to illustrate how to transform expressions involving cotangent into simpler forms using trigonometric identities, such as converting cot(x) to cos(x)/sin(x).

💡Secant

Secant, represented as 'sec', is another trigonometric function that is the reciprocal of the cosine function. The video demonstrates how secant is used in proving identities, such as in the expression 'sec(x) * csc(x)', where 'csc' is the cosecant, the reciprocal of the sine function.

💡Cosecant

Cosecant, abbreviated as 'csc', is the reciprocal of the sine function. In the video, cosecant is used in expressions that are being proven, and it is shown how to manipulate expressions involving cosecant to match the desired form using trigonometric identities.

💡Pythagorean Identities

Pythagorean identities are fundamental relationships in trigonometry that relate the squares of sine, cosine, and tangent. In the video, these identities are used to simplify expressions, such as replacing sin^2(x) + cos^2(x) with 1, which is a key step in proving the given identities.

💡Quotient Identities

Quotient identities are relationships between trigonometric functions that are reciprocals of each other. The video uses these identities to simplify expressions involving tangent and cotangent, for example, by converting tan(x) to sin(x)/cos(x) and vice versa.

💡Reciprocal Identities

Reciprocal identities in trigonometry are used to express one trigonometric function in terms of its reciprocal. In the video, these identities are crucial for transforming expressions involving secant and cosecant into their reciprocal forms, such as converting sec(x) to 1/cos(x) and csc(x) to 1/sin(x).

💡Difference of Squares

The difference of squares is a factoring technique used in algebra to simplify expressions of the form a^2 - b^2. In the video, this technique is applied to trigonometric expressions, such as sec^2(x) - 1, to simplify them into more manageable forms that can be used in proving identities.

Highlights

Introduction to proving identities in trigonometry by transforming one expression into another.

Strategy 1: Work with one side of the equation at a time, starting with the more complicated side.

Strategy 2: Look for opportunities to factor or add fractions, square binomials, or get a monomial denominator.

Strategy 3: Replace functions using fundamental trigonometric identities.

Suggestion to convert everything into sines and cosines if stuck.

Switching sides if stuck can help find a common middle point.

Example 1: Proving tan(x) + cot(x) = sec(x) * csc(x) by converting to sine and cosine.

Using quotient identities to simplify tan(x) and cot(x).

Finding a common denominator for the fractions.

Applying the Pythagorean identity to simplify the numerator.

Using reciprocal identities to match the right-hand side of the equation.

Example 2: Proving 1/(sec(x) - 1) + 1/(sec(x) + 1) = 2 * cot(x) * csc(x) by finding common denominators.

Multiplying fractions by opposite denominators to simplify.

Using the difference of squares to factor and simplify the expression.

Converting secant and tangent to sine and cosine to reach the desired form.

Example 3: Proving cos(T) / (1 - sin(T)) = (1 + sin(T)) / cos(T) by multiplying by cosine.

Using Pythagorean identity to replace cosine squared.

Factoring the difference of squares and simplifying.

Example 4: Proving cot^2(U) / (1 + csc(U)) = cot(U) * sec(U) - tan(U) by starting with the left-hand side.

Using Pythagorean identity to replace cot^2(U) and simplifying the numerator.

Switching sides and converting to sines and cosines to find a common middle point.

Final confirmation of the identity by matching both sides.

Transcripts

Browse More Related Video

Precalc 5.2 Verifying Trig Identities

How to Prove Trigonometric Identities (Precalculus - Trigonometry 24)

Verifying Trigonometric Identities

Proving Trigonometric Identities (Part 2) (5.5)

Proving Trigonometric Identities | Fundamental Trigonometric Identities | Formulas | Part 2

Tips to verifying trigonometric identities