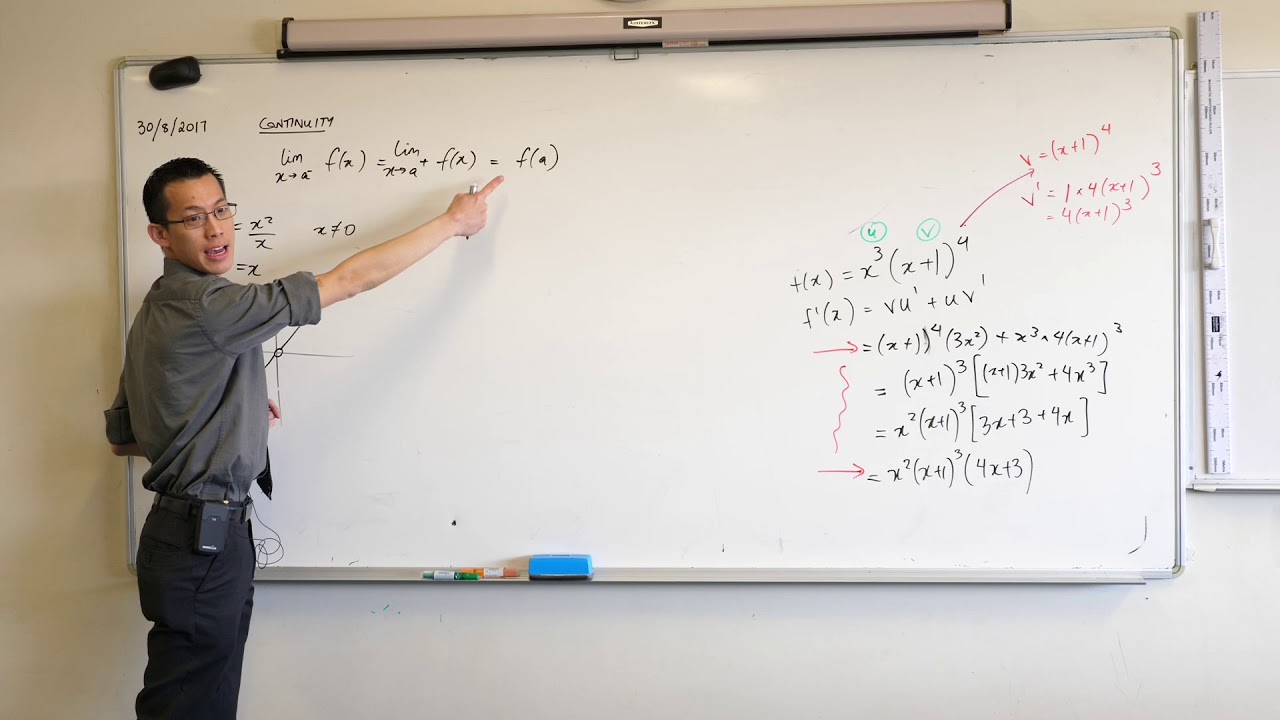What is Continuity? (1 of 2: Definitions)
TLDRThe script delves into the concept of continuity in real functions, introducing the idea with familiar shapes like straight lines and parabolas, before contrasting with discontinuous functions like the piecewise function and y=1/x, which has a 'hole' at the y-axis. It provides an informal definition of continuity as a function that can be drawn without lifting the pen, particularly focusing on the point of continuity. The formal definition of continuity is then explored using limit notation, emphasizing that for a function to be continuous at a point, the limit from the left must equal the limit from the right, and the function's value at that point. The example of y=1/x is used to illustrate testing for continuity, showing it is continuous except at x=0 where it is undefined.
Takeaways
- 📚 The script discusses the concept of continuity in real functions, introducing new ideas and notation.
- 🖊 Continuity implies that a function can be drawn without lifting the pen, indicating no breaks in the graph.
- 📉 The first non-continuous function mentioned was the piecewise function, which has gaps in its graph.
- 🔍 The function y = 1/x is highlighted as an example of a function that is continuous everywhere except at a specific point (x=0).
- 🕳 The 'big gaping hole' in the function y = 1/x is actually an infinitesimally small point, specifically the y-axis.
- ∞ The limit of y = 1/x as x approaches 0 is infinity, indicating the function's behavior near the discontinuity.
- 📝 An informal definition of continuity is provided: a function is continuous at a point if it can be drawn through that point without lifting the pen.
- 🔑 The formal definition of continuity involves the concept of limits and requires notation to express the idea precisely.
- 🔍 The formal definition states that a function is continuous at a point 'a' if the limit from the left and right approaches the function's value at 'a'.
- 📈 The script uses the function f(x) = 1/x to demonstrate how to test for continuity at a point, emphasizing that all conditions must be equal.
- 🚫 The function f(x) = 1/x is shown to be discontinuous at x=0 because the left and right limits do not equal the function's value at that point.
Q & A
What does it mean for a function to be continuous?
-A function is continuous if its graph can be drawn without lifting the pen, meaning there are no breaks or jumps in the graph at any point.
Why are straight lines, parabolas, and logarithmic functions considered continuous?
-These functions are considered continuous because they can be drawn without interruption, and you can pass through any point on their graphs without lifting the pen.
What is the first type of function that was mentioned not being continuous?
-The first non-continuous function mentioned is the piecewise function, which has breaks in its graph where the function jumps from one value to another.
What is the significance of the function y = 1/x in terms of continuity?
-The function y = 1/x is significant because it is an example of a function that is continuous everywhere except at x = 0, where it has a vertical asymptote, indicating a discontinuity.
What is the informal definition of continuity given in the script?
-The informal definition of continuity is that a function is continuous at a point if the graph can be drawn and you can go through that point without lifting your pen.
What does the formal definition of continuity involve?
-The formal definition of continuity involves the concept of limits, stating that a function is continuous at a point 'a' if the limit as x approaches 'a' from the left and from the right are equal to the function's value at 'a'.
Why is the limit as x approaches 0 of the function y = 1/x considered to be infinity?
-The limit as x approaches 0 of y = 1/x is considered to be infinity because as x gets closer to 0, the value of y grows without bound, approaching infinity.
What is the significance of the limit from the left and the limit from the right in the context of continuity?
-The significance of the limit from the left and the right is that they must both exist and be equal to the function's value at a particular point for the function to be considered continuous at that point.
Why is the function y = 1/x not continuous at x = 0?
-The function y = 1/x is not continuous at x = 0 because the limits as x approaches 0 from the left and from the right do not equal the function's value at x = 0, which is undefined.
How does the script illustrate the concept of limits in determining continuity?
-The script illustrates the concept of limits by showing that for a function to be continuous at a point, the limit as x approaches that point from both the left and the right must be equal to the function's value at that point.
What is the test case provided in the script to demonstrate the concept of continuity?
-The test case provided is the function f(x) = 1/x, which is used to demonstrate how to check for continuity at different points, such as x = 1 and x = 0.
Outlines
📚 Introduction to Continuity in Real Functions
The script introduces the concept of continuity in real functions, which is a fundamental idea leading up to calculus. It explains that continuous functions can be drawn without lifting the pen, using examples like straight lines, parabolas, and logarithms. The script then contrasts these with non-continuous functions, such as the piecewise function and y=1/x, which have 'gaping holes' at certain points. The informal definition of continuity is presented as the ability to draw the function at a point without interruption. The formal definition of continuity is then introduced using limit notation, emphasizing that the limit as x approaches a particular point from both directions must equal the function's value at that point.
🔍 Testing Continuity with the Function y=1/x
This paragraph delves deeper into the formal definition of continuity by using the function y=1/x as an example. It explains the process of testing continuity at a point by examining the limit of the function as x approaches that point from both the left and right. The script demonstrates that y=1/x is continuous at x=1 because the left and right limits equal the function's value at that point. However, it also shows that the function is not continuous at x=0, as the left and right limits approach negative and positive infinity, respectively, which do not equal the function's value at that point (undefined). The importance of approaching from both directions and the implications of the limits not matching the function's value at a point are highlighted.
Mindmap
Keywords
💡Continuity
💡Piecewise Functions
💡Limit
💡Formal Definition
💡Graph
💡Function
💡Real Functions
💡Infinitesimally Small
💡Hyperbola
💡Discontinuity
💡Approaching a Point
Highlights
Introduction to the concept of continuity in real functions, emphasizing the ability to draw a function without lifting the pen.
Differentiation between continuous functions like straight lines and parabolas, and discontinuous functions such as the step function.
The classic example of a discontinuous function, y = 1/x, which has a 'big gaping hole' at the y-axis.
Informal definition of continuity: A function is continuous at a point if it can be drawn without lifting the pen at that point.
Formal definition of continuity using limits, requiring the limit from the left and right to equal the function's value at that point.
Explanation of the limit notation and its significance in defining continuity.
The importance of approaching a point from both directions (left and right) to test for continuity.
Application of the continuity definition to the function f(x) = 1/x, demonstrating its continuity at x=1.
Testing the limit as x approaches 1 from the left and right, showing the function's value converges to 1.
Verification that f(1) = 1, confirming the function's continuity at x=1.
Contrasting the continuity at x=1 with the discontinuity at x=0 for the function f(x) = 1/x.
Analysis of the limit as x approaches 0, revealing the function approaches negative infinity from the left and positive infinity from the right.
Explanation of why the function f(x) = 1/x is discontinuous at x=0, due to the non-equal limits from the left and right.
The significance of the y-axis as the point of discontinuity for the function f(x) = 1/x.
The concept that the limit as x approaches 0 is undefined for f(x) = 1/x, indicating discontinuity.
The necessity of the limit from both directions and the function value to be equal for continuity.
The practical application of the continuity concept in analyzing the behavior of functions at specific points.
The transition from discussing continuity to preparing to introduce calculus, indicating the foundational role of continuity in advanced mathematics.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: