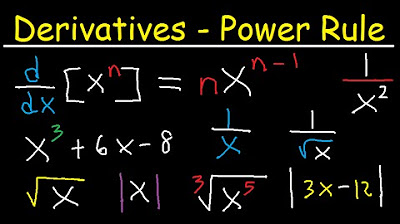Power Rule... How? (NancyPi)
TLDRIn this educational video, Nancy explains the power rule for differentiation, a fundamental shortcut in calculus that simplifies the process of finding derivatives. She demonstrates how to apply the power rule to various terms within a polynomial, including terms with positive integer powers, constants, and even negative or fractional powers. Nancy emphasizes the importance of reducing the power by one and adjusting for constants when necessary. She also clarifies the derivative of x to the first power and touches upon the sum and difference rule for combining derivatives of individual terms. The video is an engaging and informative guide for those learning calculus, aiming to demystify the power rule and its applications.
Takeaways
- 📚 The power rule is a shortcut for finding derivatives without using the formal limit definition, which is more time-consuming.
- ⚡ To apply the power rule, you bring down the power as a coefficient and decrease the power by 1 for positive integer powers of x.
- 🔢 If there's a constant multiplied by the power of x, you keep the constant and apply the power rule to the rest of the term.
- 📉 For terms with negative or fractional powers, you can apply the power rule similarly, but you need to adjust the power accordingly.
- 👉 The derivative of x to the power of 1 (x^1) is simply 1, which is a special case of the power rule.
- 🚫 When differentiating a constant term, the result is always 0, following the constant rule.
- 🔁 The sum and difference rule allows you to find the derivative of a polynomial by differentiating each term individually and then combining them.
- ⚠️ Be cautious with negative powers; reducing the power by 1 results in a more negative number.
- 🤔 For fraction powers less than 1, the derivative may not be defined at x equals 0.
- 📝 The process of finding derivatives involves applying multiple rules, such as the power rule, constant multiple rule, and sum and difference rule.
- 💡 Understanding and memorizing these rules can help streamline the process of finding derivatives for various functions.
Q & A
What is the power rule in calculus?
-The power rule is a derivative rule that allows you to find the derivative of a function in the form of x^n, where n is a positive integer. It states that the derivative of x^n is n*x^(n-1).
How does the power rule simplify the process of finding derivatives?
-The power rule simplifies the process by eliminating the need to use the formal limit definition of the derivative, which can be long and tedious. Instead, it provides a quick shortcut to find the derivative by simply bringing down the power as a coefficient and reducing the power by 1.
What is the constant multiple rule in the context of differentiation?
-The constant multiple rule states that when a constant is multiplied by a function, you can keep the constant and differentiate the rest of the function. This rule is used when differentiating terms like 2x^3, where the constant 2 is kept and the derivative of x^3 is taken.
How do you differentiate a term with a negative power using the power rule?
-When differentiating a term with a negative power, you still bring down the power as a coefficient and reduce the power by 1. However, since the power is negative, reducing it by 1 makes it even more negative. For example, the derivative of x^(-2) would be -2*x^(-3).
What happens when you differentiate a term with a fraction power?
-When differentiating a term with a fraction power, you bring down the fraction as a coefficient and subtract 1 from the original power. You may need to find a common denominator to determine the new power. If the original fraction power is less than 1, the derivative will not be defined at x=0.
What is the derivative of x to the first power?
-The derivative of x to the first power (x^1) is simply 1. This is because applying the power rule, which brings down the power and reduces it by 1, results in 1*x^(0), and since x^0 is 1, the derivative is 1.
How does the sum and difference rule apply when differentiating a polynomial?
-The sum and difference rule states that the derivative of a sum or difference of terms is the sum or difference of the derivatives of the individual terms. So, when differentiating a polynomial, you find the derivative of each term separately and then combine them to get the full derivative of the polynomial.
What is the derivative of a constant term?
-The derivative of a constant term, or a number by itself, is always 0. This is because constants do not change with respect to the variable, so their rate of change (derivative) is zero.
What is the derivative of the term 4x?
-The derivative of the term 4x is simply 4. This is derived by applying the constant multiple rule, where the constant 4 is kept and the derivative of x, which is 1, is taken.
Can you use the power rule for fractional or negative exponents?
-Yes, you can use the power rule for fractional or negative exponents as well. The process is similar: you bring down the exponent as a coefficient and reduce the power by 1. However, care must be taken when dealing with negative exponents, as reducing them by 1 results in a more negative number.
What is the significance of the power rule for positive integer powers?
-The significance of the power rule for positive integer powers is that it provides a straightforward method to find the derivatives of such terms without resorting to more complex limit definitions. It is a fundamental rule that greatly simplifies the differentiation process in calculus.
Outlines
📚 Introduction to the Power Rule
In the first paragraph, Nancy introduces the concept of the power rule, which is a derivative rule that simplifies the process of finding derivatives without resorting to the formal limit definition. She explains that the power rule is a shortcut that applies to powers of x and involves bringing the power down as a coefficient and reducing the power by 1. Nancy also mentions that she will cover derivatives of terms with fractional or negative powers and demonstrates the process by differentiating a given polynomial term by term.
🔢 Applying the Power Rule and Constant Multiple Rule
The second paragraph delves into applying the power rule to various terms within a polynomial. Nancy shows how to handle terms with constants multiplied by x, using the constant multiple rule to keep the constant and then apply the power rule to the rest of the term. She also covers the derivative of x to the power of 1, which is simply 1, and explains the reasoning behind it. Additionally, she addresses the derivative of a constant term, which is always 0, according to the constant rule. Nancy concludes by emphasizing the sum and difference rule, which allows for the differentiation of each term individually and then combining them for the full derivative.
Mindmap
Keywords
💡Power Rule
💡Derivative
💡Polynomial
💡Constant Multiple Rule
💡Fractional Powers
💡Negative Powers
💡Sum and Difference Rule
💡Constant Rule
💡Limit Definition
💡Coefficient
💡Common Denominator
Highlights
The power rule is a shortcut for finding derivatives without using the formal limit definition, which is long and tedious.
The power rule applies to polynomials with terms added or subtracted - find the derivative of each term individually.
For a term like x^4, bring down the power (4) to the front as a coefficient and reduce the power by 1 to get x^3.
The power rule formula: derivative of x^n is n*x^(n-1), where n is a positive integer power.
If there is a constant multiplied by the term, keep the constant and apply the power rule to the rest of the term.
For a term like 2x^3, keep the 2, apply the power rule to x^3 to get 2*3*x^2 = 6x^2.
The derivative of x^2 is 2x by bringing down the power and reducing it by 1.
For a term like 4x, the derivative is just the number 4 since the derivative of x is 1.
The derivative of a constant term like -1 is 0, following the constant rule.
To find the full derivative, differentiate each term individually and sum/subtract them following the sum/difference rule.
For negative powers, bring down the power, reduce it by 1, and be careful of the resulting more negative number.
For fractional powers, bring down the power as a coefficient, subtract the original power by 1, and find a common denominator.
If the original fractional power is less than 1, the resulting derivative will not be defined at x=0.
The power rule is a fast and simple method for finding derivatives of terms with powers of x.
The constant multiple rule allows you to keep a constant and apply the power rule to the rest of the term.
The sum/difference rule lets you find the full derivative by differentiating each term individually and combining them.
The power rule can also be applied to negative and fractional powers with some adjustments.
The video provides a clear, step-by-step explanation of how to use the power rule for different types of terms.
The presenter uses a specific polynomial example to demonstrate how to apply the power rule to each term.
The video also covers important related concepts like the constant multiple rule and sum/difference rule.
The presenter provides helpful tips and warnings about applying the power rule to negative and fractional powers.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: