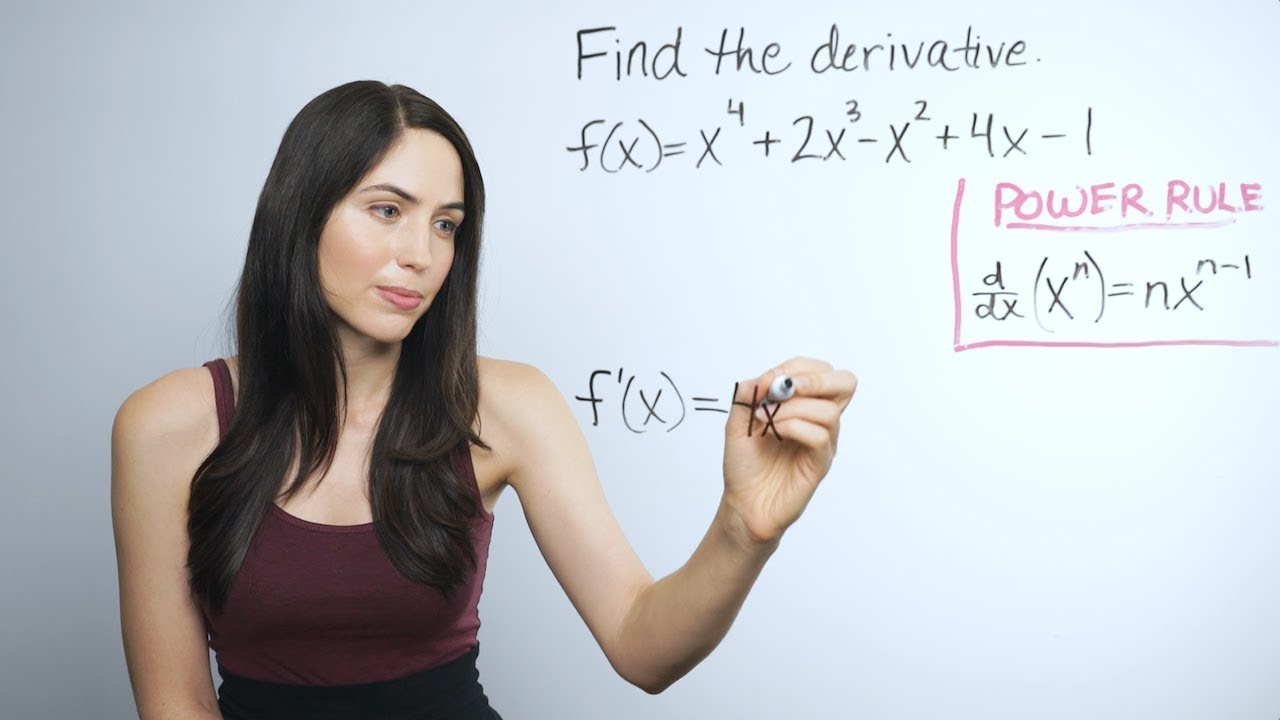Calculus - How to find the derivative of a function using the power rule

MySecretMathTutor
4 Sept 201305:21
EducationalLearning
32 Likes 10 Comments

TLDRIn this tutorial, the power rule for finding derivatives is introduced, a fundamental concept in calculus. The rule is applicable to functions where x is raised to a non-zero power, simplifying the process by dropping the power as a coefficient and reducing the exponent by one. Examples illustrate the rule's application, including handling coefficients and combining terms with addition or subtraction. The video also covers the power rule's extension to negative and fractional powers, demonstrating its versatility in various mathematical scenarios.

Takeaways
  • 📚 The power rule is a fundamental method for finding the derivative of a function where the variable x is raised to a power.
  • 🔢 The rule applies when the power is not zero, as the derivative of a constant (x^0) is not subject to the power rule.
  • 📉 To apply the power rule, you drop the power in front of the derivative and reduce the power by one.
  • 📈 The power rule is demonstrated through examples, showing its application to functions like x^5 and x^4.
  • 🔄 When coefficients are present, they can be moved in front of the derivative without altering the rule's application.
  • 📝 The derivative of a function with multiple terms, such as 4x^3 - 5x^4, is found by applying the power rule to each term individually.
  • 🤔 The power rule can be applied to negative and fractional powers, with the same principles of reducing the power by one.
  • 📉 The script emphasizes the importance of understanding the power rule's application to various powers, including those that are not integers.
  • 👍 The power rule is described as powerful and effective, capable of simplifying the process of finding derivatives.
  • 📚 The tutorial provides a step-by-step guide on how to apply the power rule, enhancing understanding through multiple examples.
  • 👏 The video concludes by encouraging viewers to look for opportunities to apply the power rule in various mathematical scenarios.
Q & A

  • What is the power rule for finding derivatives?

    -The power rule states that for a function f(x) = x^n, where n is a power and not equal to zero, the derivative f'(x) is n * x^(n-1).

  • Why can't the power rule be applied when the power is zero?

    -When the power is zero, the function becomes a constant, and the derivative of a constant is zero, so the power rule is not applicable.

  • What is the derivative of f(x) = x^5 according to the power rule?

    -The derivative of f(x) = x^5 is 5x^4, obtained by taking the power 5, placing it in front, and then reducing the power by one.

  • How do you handle coefficients in front of the variable when using the power rule?

    -You can move the coefficients in front of the variable to the front of the derivative and then apply the power rule to the variable part.

  • What is the derivative of f(x) = 3x^2 if you apply the power rule?

    -The derivative of f(x) = 3x^2 is 6x, by taking the coefficient 3, placing it in front, and then reducing the power of x from 2 to 1.

  • Can the power rule be used with negative powers?

    -Yes, the power rule can be used with negative powers, and it works in the same way as with positive powers.

  • What is the derivative of f(x) = 4x^3 - 5x^4 using the power rule?

    -The derivative of f(x) = 4x^3 - 5x^4 is 12x^2 - 20x^3, by applying the power rule to both terms separately.

  • How does the power rule apply to fractional powers?

    -The power rule applies to fractional powers in the same manner as to integer powers, by taking the fractional power, placing it in front, and then reducing it by one.

  • What is the derivative of f(x) = (3x^(-1/2)) if you apply the power rule?

    -The derivative of f(x) = (3x^(-1/2)) is -3/2 * x^(-3/2), by taking the power -1/2, placing it in front as -1/2, and then reducing it by one to get -3/2.

  • Can you combine the power rule with other operations in a function?

    -Yes, the power rule can be combined with other operations such as addition and subtraction within a function, and it can be applied term by term.

  • What is the derivative of a function that has both positive and negative powers of x?

    -The derivative of such a function is found by applying the power rule to each term with x raised to a power, regardless of whether the power is positive or negative.

Outlines
00:00
📚 Introduction to the Power Rule for Derivatives

This paragraph introduces the power rule for finding the derivative of a function, which is fundamental in calculus. The power rule is applicable when a variable, such as x, is raised to a power and is not equal to zero. The rule involves dropping the power as a coefficient in front of the variable and then reducing the power by one. The paragraph promises to demonstrate this rule with various examples to show its effectiveness and simplicity despite the initial complexity of the notation.

05:04
🔍 Applying the Power Rule with Examples

The paragraph provides a step-by-step application of the power rule to different functions, including those with coefficients and powers. It starts with a simple example of the derivative of x to the fifth power, then moves on to include coefficients, such as in 3x squared. The paragraph also explains how to deal with functions that have multiple terms, like 4x cubed minus 5x to the fourth, by applying the power rule to each term separately. The explanation emphasizes the rule's versatility and its ability to handle a wide range of powers, including negative and fractional exponents.

📘 Advanced Application of the Power Rule

This final paragraph delves into more complex examples that involve negative and fractional powers, demonstrating the power rule's universality. The explanation shows how coefficients act similarly to constants and can be factored out, while the power is reduced by one regardless of whether it is negative or a fraction. The paragraph concludes with a detailed example that includes both negative and fractional powers, illustrating the rule's consistent application and the importance of carefully reducing the power by one in each case.

Mindmap
Keywords
💡Derivative
The derivative in calculus is a measure of how a function changes as its input changes. It is the rate at which the output of the function changes with respect to the change in its input. In the video, the derivative is the main focus, with the power rule being the method to find it. For example, when the function is 'f(x) = x^5', the derivative is found to be '5x^4' using the power rule.
💡Power Rule
The power rule is a fundamental principle in calculus for finding the derivative of a function that involves a variable raised to a power. It states that if you have a function in the form of 'f(x) = x^n', the derivative is 'n * x^(n-1)'. The video uses the power rule to demonstrate how to find derivatives of various functions, emphasizing its effectiveness and simplicity.
💡Constant
In calculus, a constant is a value that does not change. The video mentions that if the power to which 'x' is raised is zero, the function is a constant, and the derivative of a constant is zero. This is because constants do not change with respect to the variable, hence their rate of change is zero.
💡Coefficient
A coefficient is a numerical factor that multiplies a variable in an algebraic expression. In the context of the video, coefficients like '3' and '4' are mentioned, which are then factored out when applying the power rule to functions like '3x^2' and '4x^3', simplifying the process of finding the derivative.
💡Variable
A variable in mathematics is a symbol that represents an unknown or changeable value. In the video, 'x' is the variable, and the power rule is applied to functions of 'x' raised to various powers to find their derivatives. The variable 'x' is central to the concept of differentiation.
💡Function
A function in mathematics is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output. The video discusses finding the derivative of functions, which is a fundamental operation in calculus to understand the behavior of functions.
💡Differentiation
Differentiation is the process of finding the derivative of a function. It is a key concept in calculus and is used to analyze the behavior of functions, such as their rate of change at a particular point. The video's theme revolves around teaching differentiation using the power rule.
💡Negative Power
A negative power indicates that a number is raised to the reciprocal of a positive integer. In the video, the power rule is applied to functions with negative powers, such as 'x^(-2)', demonstrating that the rule is versatile and can handle various types of powers, including negative ones.
💡Fractional Power
A fractional power is a power that is not a whole number. The video shows that the power rule can be applied to functions with fractional powers, such as 'x^(1/2)', by bringing the fractional power to the front and reducing it by one, just as with integer powers.
💡Example
Examples in the video are used to illustrate the application of the power rule in finding derivatives. Each example demonstrates a different scenario, such as a function with a single term or multiple terms with coefficients and powers, helping viewers understand how to apply the rule in various situations.
💡Simplification
Simplification in mathematics is the process of making an expression easier to understand or work with. The video mentions simplification after applying the power rule, such as reducing the power of 'x' by one and multiplying coefficients, to arrive at the final form of the derivative.
Highlights

Introduction to the power rule for finding derivatives.

The power rule is applicable for functions where X is raised to a non-zero power.

The rule involves dropping the power in front and reducing the exponent by one.

Example given: Derivative of X to the fifth power results in 5X to the fourth power.

Coefficients in front of the function can be moved outside the derivative calculation.

Demonstration of applying the power rule to a function with multiple terms, such as 4X cubed minus 5X to the fourth.

The power rule is effective for both addition and subtraction within functions.

Explanation of how to handle negative and fractional powers using the power rule.

Example of applying the power rule to a function with negative and fractional powers.

The importance of reducing the power by one, regardless of whether it's negative or a fraction.

Final simplification of derivatives involving coefficients and powers.

The power rule's utility in various mathematical situations is emphasized.

The video provides a clear demonstration of the power rule's application to multiple examples.

The power rule is a fundamental concept in calculus for finding derivatives.

The video concludes with a summary of the power rule's effectiveness and versatility.

Transcripts

Browse More Related Video

Power Rule... How? (NancyPi)

Derivatives - Power Rule

Math 1325 Lecture 9 4 - Derivative Formulas

1.5 - The Power and Sum Difference Rules

Basic Derivative Rules - Part 1

Chain Rule with the Quotient Rule Problem 3 (Calculus 1)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Derivative RuleMathematics TutorialPower RuleCalculus BasicsEducational ContentStudent ResourceMath MasteryTutoring TipsLearning ToolsMath Tricks