Chain Rule with the Quotient Rule Problem 3 (Calculus 1)

BlackTshirtMathProfessor
12 Jul 202109:14
EducationalLearning
32 Likes 10 Comments

TLDRIn this engaging video, the presenter dives into a complex calculus problem that involves the application of both the quotient rule and the chain rule. The problem focuses on differentiating a quotient of functions, where the numerator is simply x and the denominator is the square root of x squared plus 1. The video demonstrates the process of finding the derivatives of the individual functions, applying the general power rule for the chain rule, and then combining these derivatives using the quotient rule. The presenter emphasizes the importance of simplifying the expression, which includes rewriting negative powers as fractions and multiplying by the least common denominator to eliminate fractions within fractions. The final simplified derivative is expressed with the numerator as one and the denominator as x squared plus one, raised to the power of three halves. This problem serves as an excellent example of the standard algebraic simplifications encountered in calculus and is a staple in the presenter's calculus course and exams.

Takeaways
  • 📚 The video discusses a problem involving the calculation of a derivative using both the quotient rule and the chain rule.
  • 🔢 The function given is a quotient of two expressions, where the numerator is simply x and the denominator is the square root of (x^2 + 1).
  • 📝 The derivative of the numerator (f') is straightforward and equals 1.
  • ⛓ The derivative of the denominator (g') requires the use of the chain rule and the general power rule, resulting in (1/2) * 2x = x.
  • 🧩 Simplifying the expression involves canceling out terms and rewriting negative exponents as fractions to handle complex fractions.
  • 🔄 The video emphasizes the importance of algebraic simplification, which is a key skill in calculus.
  • 📉 The derivative of g, when simplified, is found to be (x/(sqrt(x^2 + 1))), coincidentally the same as the original function but with a negative exponent.
  • 🤝 The quotient rule is applied to combine the derivatives of the numerator and the denominator, resulting in a fraction that needs further simplification.
  • 📌 Multiplying the numerator and denominator by the least common denominator (LCD), which is (sqrt(x^2 + 1)), helps to simplify the expression.
  • 📐 After simplification, the final form of the derivative is (1/((x^2 + 1)^(3/2))).
  • 💡 The video concludes by highlighting the problem's value for practicing both the quotient and chain rules, as well as algebraic manipulation, which are essential for calculus students.
Q & A

  • What mathematical rules are combined in the problem discussed in the video?

    -The problem combines the quotient rule and the chain rule to calculate a derivative.

  • What is the function f(x) in the problem?

    -The function f(x) is simply x, which is the numerator of the given quotient.

  • What is the function g(x) in the problem?

    -The function g(x) is the square root of x squared plus 1, which is the denominator of the given quotient.

  • How is the derivative of f(x) calculated?

    -The derivative of f(x), which is x, is calculated to be 1, as the derivative of x with respect to x is 1.

  • What is the general power rule used to calculate g'(x)?

    -The general power rule is used by rewriting g(x) as (x^2 + 1)^(1/2) and then differentiating it, bringing the exponent down and multiplying by the derivative of the inside function, which is 2x.

  • How is the quotient rule applied in this problem?

    -The quotient rule is applied by combining the derivatives of the numerator (f'(x)) and the denominator (g'(x)) and simplifying the expression, which includes subtracting the product of f(x) and g'(x) from the product of f'(x) and g(x), all divided by g(x) squared.

  • What is the significance of simplifying the expression after applying the quotient rule?

    -Simplifying the expression is crucial for clarity and to avoid confusion with fractions within fractions. It also makes the derivative easier to understand and use in further calculations.

  • Why is it beneficial to multiply the numerator and denominator by the LCD (Least Common Denominator)?

    -Multiplying by the LCD simplifies the expression by eliminating fractions within fractions, making it easier to combine like terms and simplify the overall derivative.

  • What is the final simplified form of the derivative found in the problem?

    -The final simplified form of the derivative is 1 divided by (x^2 + 1)^(3/2).

  • Why is this problem considered a good example for a calculus course?

    -This problem is considered good for a calculus course because it involves the application of the quotient rule and the chain rule, and it requires standard algebraic simplifications that are common in calculus.

  • What is the role of the chain rule in differentiating g(x) in this problem?

    -The chain rule is used to differentiate g(x) because g(x) is a composite function. It allows the differentiation of the outer function (the square root) while considering the derivative of the inner function (x^2 + 1).

  • How does the video script help students get comfortable with complex fraction expressions?

    -The video script helps students by demonstrating the process of rewriting negative powers as fractions and then simplifying complex fractions expressions step by step, which is a common technique used in calculus.

Outlines
00:00
🧮 Application of Quotient and Chain Rules in Calculus

This paragraph introduces a calculus problem that involves the use of both the quotient rule and the chain rule to calculate a derivative. The function in question is a quotient of two expressions, with the numerator being a simple x and the denominator being the square root of (x^2 + 1). The presenter explains the process of identifying the necessary components for the quotient rule and then differentiating the denominator using the chain rule. The derivatives of both the numerator (f') and the denominator (g') are calculated, with special attention given to the general power rule for differentiating the denominator. The paragraph concludes with the presenter simplifying the derivative expression by combining the pieces back together according to the quotient rule and rewriting negative powers as fractions for further simplification.

05:00
📐 Simplifying Complex Fractions in Derivatives

The second paragraph delves into the simplification of the derivative obtained from the previous paragraph. The presenter emphasizes the complexity of the expression due to fractions within fractions and suggests a method for simplification. This involves multiplying both the numerator and denominator by the least common denominator (LCD), which in this case is the square root of (x^2 + 1). The presenter demonstrates how this step leads to the cancellation of terms and a simplified expression. The focus is on the algebraic simplification process, which is a critical skill for calculus students. The final simplified form of the derivative is expressed with the numerator as 1 and the denominator as (x^2 + 1)^(3/2). The paragraph concludes with the presenter's recommendation of this problem type for inclusion in calculus courses and exams due to its comprehensive coverage of important calculus concepts.

Mindmap
Keywords
💡Derivative
A derivative in calculus represents the rate at which a function changes with respect to its variable. It is a fundamental concept used to analyze the behavior of functions. In the video, the process of calculating derivatives is central to the problem-solving, particularly using the quotient rule and chain rule.
💡Quotient Rule
The quotient rule is a mathematical theorem that allows for the calculation of the derivative of a quotient of two functions. It is expressed as (f/g)' = (g*f' - f*g') / (g^2). The video discusses applying the quotient rule to a function that is a quotient of x and the square root of x squared plus 1.
💡Chain Rule
The chain rule is a fundamental theorem used for finding the derivative of a composite function. It states that the derivative of a composite function is the derivative of the outer function times the derivative of the inner function. In the video, the chain rule is applied when differentiating the square root of x squared plus 1.
💡General Power Rule
The general power rule is a specific case of the chain rule used when differentiating power functions. It states that the derivative of x to the power of n is n times x to the power of n minus one. In the video, this rule is used to differentiate the square root of x squared plus 1, rewriting it as x squared plus 1 to the power of one half.
💡Simplifying Expressions
Simplifying expressions is a crucial step in calculus that involves reducing complex expressions to a more straightforward form. The video emphasizes the importance of simplifying the derivative expressions, especially when dealing with fractions and negative exponents, to make them easier to understand and work with.
💡Composite Function
A composite function is a function that is made by combining two or more functions. In the context of the video, the function g(x) = sqrt(x^2 + 1) is a composite function because it involves the square root of another function (x^2 + 1).
💡Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. In the video, the square root is used within the function g(x) and its derivative, where it is simplified and manipulated to find the derivative of the composite function.
💡Negative Exponents
Negative exponents indicate the reciprocal of a number raised to the corresponding positive exponent. In the video, negative exponents are encountered when rewriting the derivative of g(x), and they are simplified by converting them into fractions to deal with complex fractions more effectively.
💡Fractions within Fractions
A fraction within a fraction, also known as a complex fraction, occurs when a fraction is the numerator or denominator of another fraction. The video discusses a method to simplify such expressions by multiplying the numerator and denominator by the least common denominator (LCD), which simplifies the calculation.
💡Least Common Denominator (LCD)
The least common denominator is the smallest multiple that each of the denominators of a set of fractions can divide into. In the video, the LCD is used as a tool to simplify complex fractions by eliminating the fractions within fractions, making the derivative easier to solve and understand.
💡Algebraic Simplification
Algebraic simplification involves using algebraic techniques to reduce an expression to a simpler form. The video highlights the importance of algebraic simplification in calculus, especially when working with quotients and derivatives, to arrive at a more manageable and understandable result.
Highlights

The video focuses on a problem that combines the quotient rule and chain rule for calculating derivatives.

The function in question is a quotient of x and the square root of x squared plus 1.

Derivative of the numerator (f'(x)) is simply 1.

Derivative of the denominator (g'(x)) involves applying the chain rule to (x^2 + 1)^(1/2).

The general power rule is used to simplify the derivative of the denominator.

The quotient rule is applied to combine the derivatives of the numerator and the denominator.

Simplification involves rewriting negative exponents as fractions to handle complex fractions.

The derivative of g(x) turns out to be similar to the original function, which is a coincidence.

The quotient rule is carefully applied, factoring in the square root form of the denominator's derivative.

The video emphasizes the importance of algebraic simplification in calculus problems.

Multiplying by the least common denominator (LCD) simplifies the fraction within a fraction.

The final simplified form of the derivative is obtained by canceling out terms and combining exponents.

The video concludes with the final simplified derivative in terms of x and (x^2 + 1)^(3/2).

The problem is a good example of the application of the quotient rule and chain rule, emphasized by its inclusion in calculus courses and exams.

The video is educational, aiming to help students get comfortable with simplifying complex fractions in calculus.

The presenter suggests that this type of problem is beneficial for standard algebraic simplifications that students will encounter.

The video is part of a series that supports learning in a calculus course, particularly focusing on derivative rules.

Viewers are encouraged to like, subscribe, and support the channel for more educational content.

Transcripts

Browse More Related Video

Math 1325 Lecture 9 5 - Product & Quotient Rule

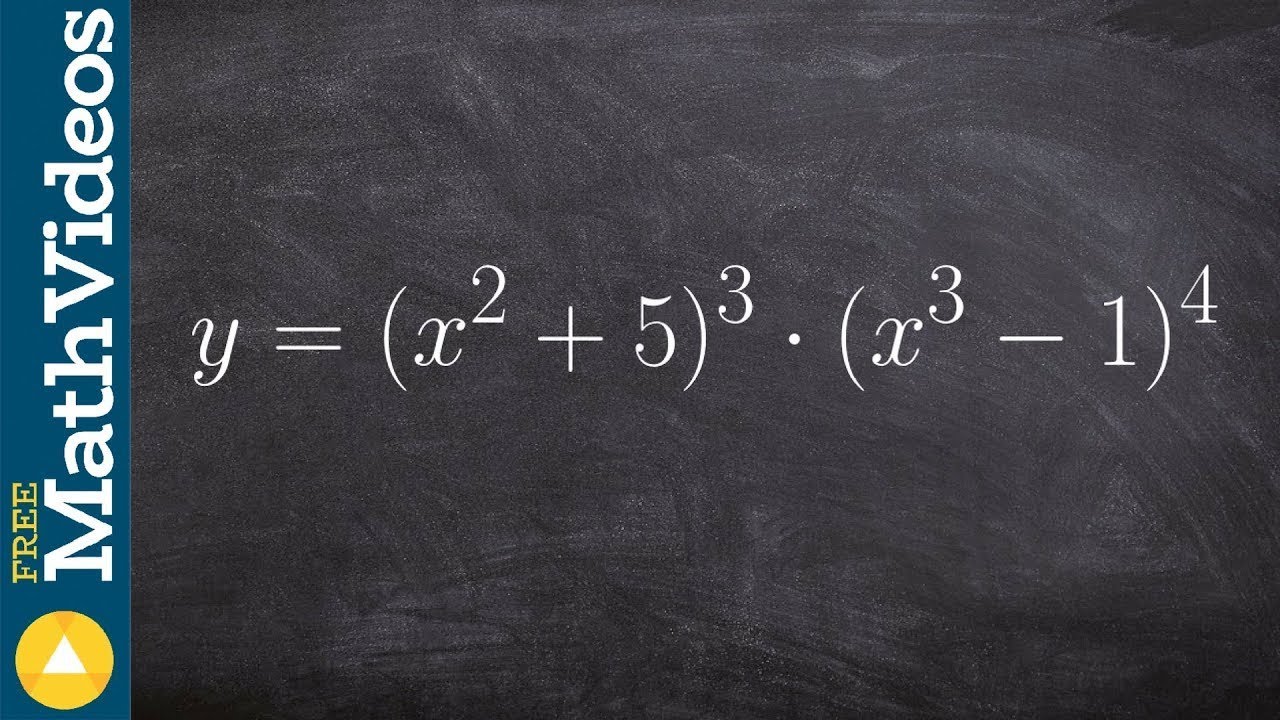
Taking the derivative of two binomials using product and chain rule

Math 1325 Lecture 9 7 - Using Derivative Forumulas

Quotient rule from product & chain rules | Derivative rules | AP Calculus AB | Khan Academy

Logarithmic functions differentiation | Advanced derivatives | AP Calculus AB | Khan Academy

Simplifying Derivatives

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusDerivativeQuotient RuleChain RuleMathematicsSimplificationAlgebraEducationComplex FractionsPower RuleLearning