Area vector with examples & flux vector equation | Electric fields & charges | Khan Academy

Khan Academy India - English

14 Oct 202112:18

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video script delves into the concept of treating area as a vector in physics, particularly for calculating flux in an electric field. It clarifies the purpose of this approach, which simplifies communication and calculations. The script guides through visualizing area vectors by drawing perpendiculars, establishing a standard for closed surfaces where outward vectors are preferred. It also emphasizes the importance of correctly identifying the angle theta between the electric field and the area vector, demonstrating how this leads to a more efficient calculation of flux using the dot product notation, e·a.

Takeaways

📚 Converting area into a vector simplifies communication in physics, particularly when calculating flux.
🔍 The concept of area as a vector helps to reduce the complexity of describing the perpendicular component of an area to an electric field.
📐 The direction of the area vector is always perpendicular to the surface of the area.
🌐 The magnitude of the area vector is proportional to the size of the area it represents.
🧭 For closed surfaces, the standard direction for the area vector is outward from the surface.
🔄 For open surfaces, the direction of the area vector can be arbitrary, but it's often chosen to be perpendicular to the surface.
🤔 The choice of direction for the area vector on open surfaces is not standardized due to the lack of an 'outward' or 'inward' concept.
📈 In physics, when dealing with flux, the angle theta is defined as the angle between the electric field vector and the area vector.
📝 Flux can be calculated more efficiently using the dot product of the electric field vector and the area vector, represented as e dot a.
🚫 A common mistake is to confuse the angle theta with the angle between the area and the perpendicular component, rather than the angle between the electric field and the area vector.
🔑 Understanding the direction and magnitude of the area vector is crucial for accurately calculating physical quantities like flux.

Q & A

Why is area sometimes treated as a vector in physics?
-Area is treated as a vector in physics to simplify communication and calculations, especially when calculating quantities like flux, which is the product of an electric field and the perpendicular component of an area.
What is the significance of treating area as a vector for the calculation of flux?
-Treating area as a vector simplifies the calculation of flux by allowing the use of vector notation and operations, such as the dot product, which is more efficient than describing the perpendicular component with words.
How is the direction of an area vector determined?
-The direction of an area vector is determined by drawing a vector perpendicular to the area. For closed surfaces, the standard direction is outward, while for open surfaces, the direction can be arbitrary.
What is the relationship between the angle theta in the context of flux and the area vector?
-Theta is the angle between the electric field vector and the area vector. It is used to calculate the component of the area that is perpendicular to the electric field, which is essential for flux calculations.
Why is it difficult to standardize the direction of an area vector for open surfaces?
-For open surfaces, there is no inherent 'outward' or 'inward' direction, making it difficult to standardize the direction of the area vector. However, for closed surfaces, the standard is to choose the outward direction.
What is the advantage of using the dot product notation for calculating flux?
-Using the dot product notation simplifies the expression of flux to a single term, 'e dot a', making it easier to communicate and calculate, especially in complex three-dimensional scenarios.
Can you give an example of how to calculate the flux through an area given the electric field and the angle?
-To calculate the flux, you would use the formula flux = e * a * cos(theta), where 'e' is the magnitude of the electric field, 'a' is the magnitude of the area, and 'theta' is the angle between the electric field vector and the area vector.
What is the common mistake made when calculating the angle theta for flux calculations?
-A common mistake is to confuse theta with the angle between the electric field and the surface itself, rather than the angle between the electric field vector and the area vector.
How does treating area as a vector help in the context of a closed surface?
-For closed surfaces, treating area as a vector with an outward direction standardizes the direction of the area vector, simplifying calculations and communication in physics.
What is the significance of the perpendicular component of the area in flux calculations?
-The perpendicular component of the area is significant because it represents the part of the area that is effective in the flux calculation, being directly exposed to the electric field.

Outlines

00:00

📚 Introduction to Area as a Vector

The script begins by introducing the concept of treating area as a vector, particularly in the context of physics. It questions the rationale behind converting area into a vector and explains that it simplifies communication in physics, specifically when calculating flux. The script uses the example of an electric field and area to illustrate how flux is calculated as the product of the electric field and the perpendicular component of the area. It contrasts the verbosity of traditional explanations with the conciseness offered by treating area as a vector, highlighting the efficiency of mathematical symbols and equations.

05:00

🧭 Directionality of Area Vectors

This paragraph delves into the specifics of how to determine the direction of an area vector. It suggests that the direction is always perpendicular to the area in question, with the magnitude of the vector being proportional to the size of the area. The script provides examples of rectangular and circular areas to demonstrate how to visualize and determine the direction of the area vector. It also addresses the ambiguity of choosing a direction for open surfaces, where it can be arbitrary, contrasting this with the standardized outward direction for closed surfaces in physics.

10:02

🔍 Clarifying Flux Calculation with Area Vectors

The final paragraph focuses on the practical application of area vectors in calculating flux. It emphasizes the ease of communication and calculation when using the dot product notation, which represents the flux as the product of the electric field vector and the area vector, taking into account the cosine of the angle between them. The script corrects a common mistake regarding the interpretation of the angle theta, clarifying that it is the angle between the electric field vector and the area vector, not the angle between the field and the surface itself. It concludes with an example calculation of flux, reinforcing the importance of understanding the correct angle for accurate computation.

Mindmap

Keywords

💡Area Vector

An 'Area Vector' is a concept where a flat, two-dimensional area is treated as if it has a direction, represented by a vector that is perpendicular to the area. In the video, the area vector is introduced to simplify the communication of physical phenomena, such as calculating flux in physics. The script uses the area vector to demonstrate how the perpendicular component of an area can be more efficiently communicated through vector notation rather than using trigonometric explanations.

💡Flux

Flux, in physics, refers to the rate of transfer of a property (such as heat, energy, or the number of particles) across a unit area. The video script explains how flux can be calculated using the dot product of the electric field vector and the area vector, which simplifies the process of determining the perpendicular component of the area with respect to the electric field.

💡Electric Field

An 'Electric Field' is a field that surrounds electrically charged particles and exerts force on other charged particles within the field. In the context of the video, the electric field is used as an example to illustrate the calculation of flux, where the electric field vector is multiplied by the area vector to find the flux through a given area.

💡Perpendicular Component

The 'Perpendicular Component' of a vector or area is the part of it that is at a right angle (90 degrees) to another vector or direction. The script explains that treating area as a vector helps in identifying and calculating this component, which is crucial for determining flux in the presence of an electric field.

💡Dot Product

The 'Dot Product', also known as the scalar product, is an algebraic operation that takes two equal-length vectors and returns a single number (scalar). In the video, the dot product is used to express the calculation of flux as the product of the electric field vector and the area vector, where the cosine of the angle between them is implicitly accounted for.

💡Trigonometry

Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles. The script initially mentions using trigonometry to calculate flux with the formula involving the electric field, area, and the cosine of the angle (theta) between them, but later argues for the simplicity of using vectors and the dot product instead.

💡Theta (θ)

In the script, 'Theta' (θ) represents the angle between the electric field vector and the area vector. It is initially described in a trigonometric context but is later redefined in a vector context as the angle that simplifies the calculation of flux, emphasizing the efficiency of vector notation over trigonometric explanations.

💡Closed Surface

A 'Closed Surface' is a surface that completely encloses a volume, with no open edges or boundaries. The video script discusses how, when dealing with closed surfaces, the direction of the area vector can be standardized as outward, which simplifies calculations and understanding in physical scenarios.

💡Open Surface

An 'Open Surface' is a surface that does not enclose a volume and has boundaries or edges. The script explains that for open surfaces, the direction of the area vector can be arbitrary since there is no inherent 'outward' or 'inward' direction, contrasting with the standardization possible with closed surfaces.

💡Directional Standardization

In the context of the video, 'Directional Standardization' refers to the convention of choosing a consistent direction for area vectors, particularly for closed surfaces where the outward direction is chosen by default. This standardization aids in simplifying the calculations and communication in physics.

Highlights

Area can be treated as a vector to simplify communication in physics, particularly in calculating flux.

Flux is calculated as the product of the electric field and the perpendicular component of the area.

Converting area to a vector reduces the need for complex language and makes equations more concise.

The direction of the area vector is perpendicular to the surface of the area.

The magnitude of the area vector is proportional to the size of the area.

For closed surfaces, the standard direction for area vectors is outward.

The angle theta in flux calculations is the angle between the electric field vector and the area vector.

Flux can be efficiently expressed as the dot product of the electric field vector and the area vector.

The direction of the area vector for open surfaces is arbitrary, but for closed surfaces, it's standardized as outward.

Understanding the angle between vectors simplifies the calculation of flux.

The concept of area as a vector is particularly useful in physics for calculating flux through various surfaces.

When treating area as a vector, the direction is determined by drawing a perpendicular to the surface.

The area vector helps in reducing the complexity of expressing the perpendicular component of area in equations.

In physics, the area vector is often used in the context of closed surfaces where the outward direction is preferred.

The area vector concept simplifies the geometric interpretation of flux calculations.

A common mistake is to confuse the angle of the area vector with the angle between the electric field and the surface normal.

The example of a cylinder demonstrates the importance of choosing the outward direction for the area vector.

The area vector approach to flux calculation is more efficient and less wordy than traditional methods.

Transcripts

Browse More Related Video

Electric Flux

Electric flux meaning (& how to calculate it) | Electrostatics | Physics | Khan Academy

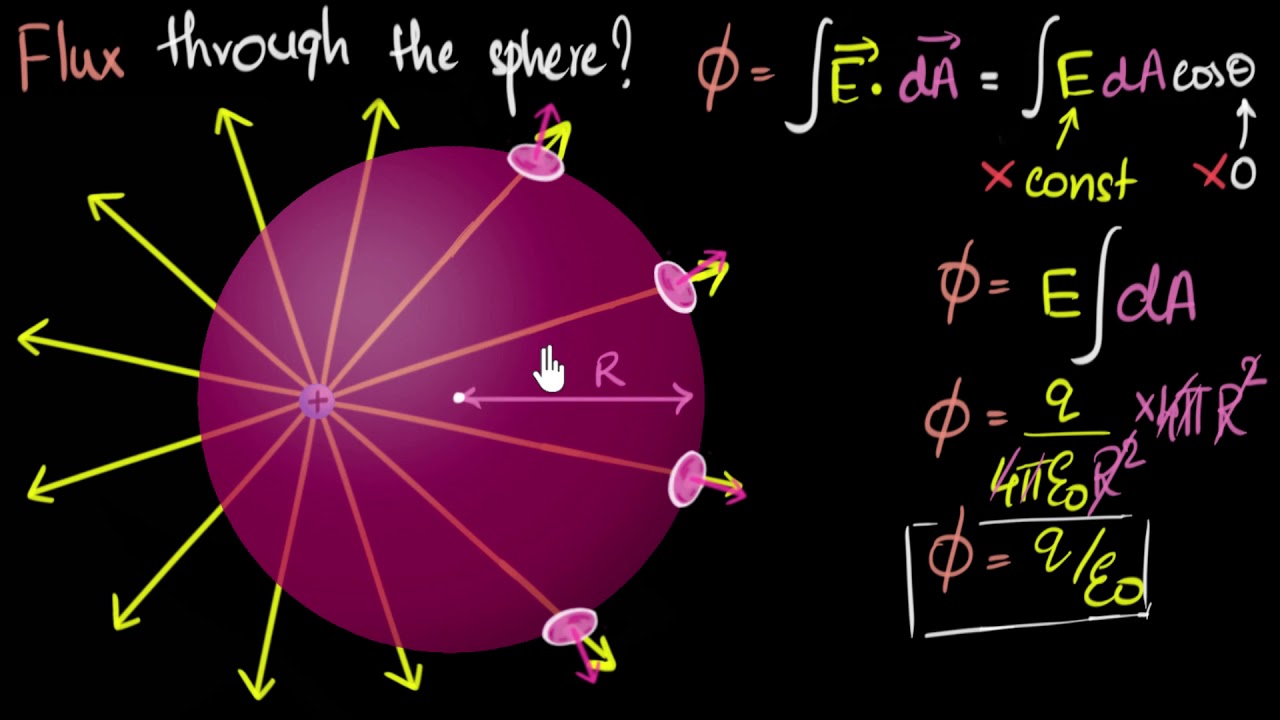
Gauss law of electricity | Electrostatics | Physics | Khan Academy

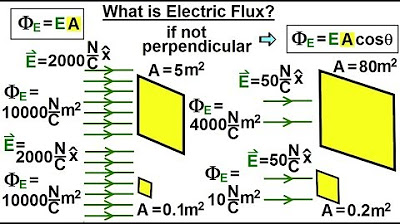
Physics 37.1 Gauss's Law Understood (2 of 29) What is Electric Flux?

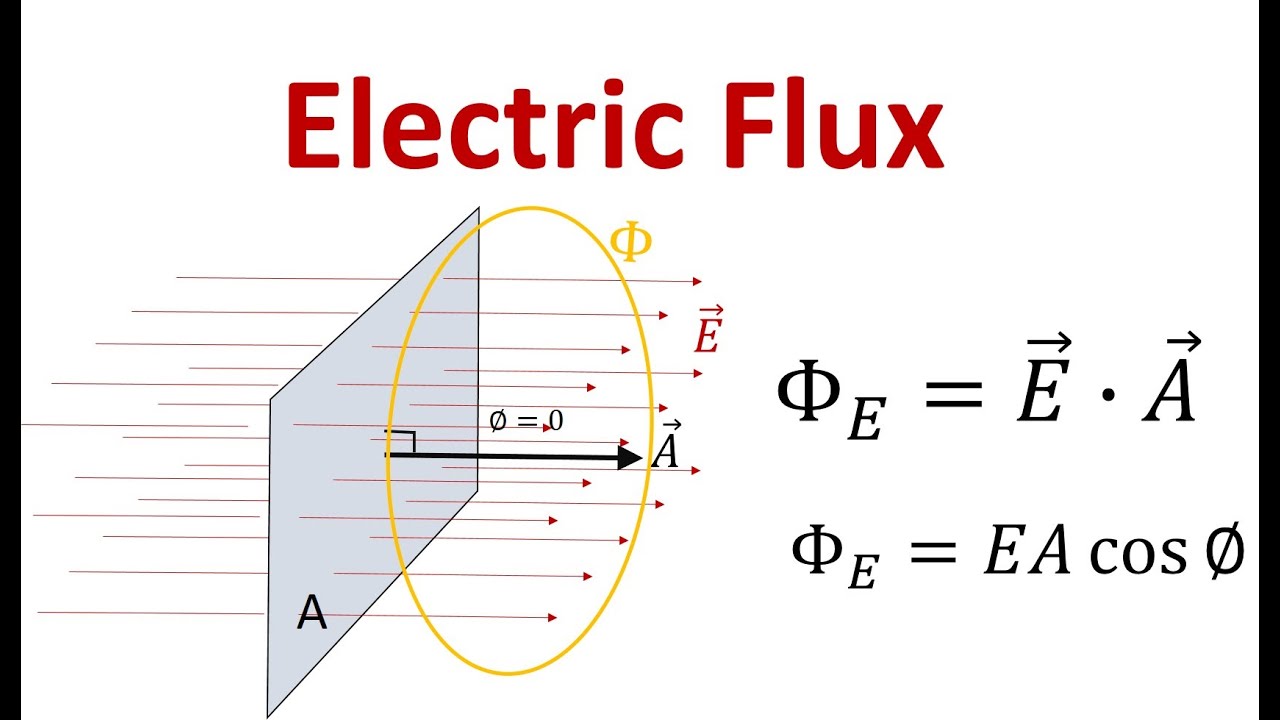
The Electric Flux and It's Applications

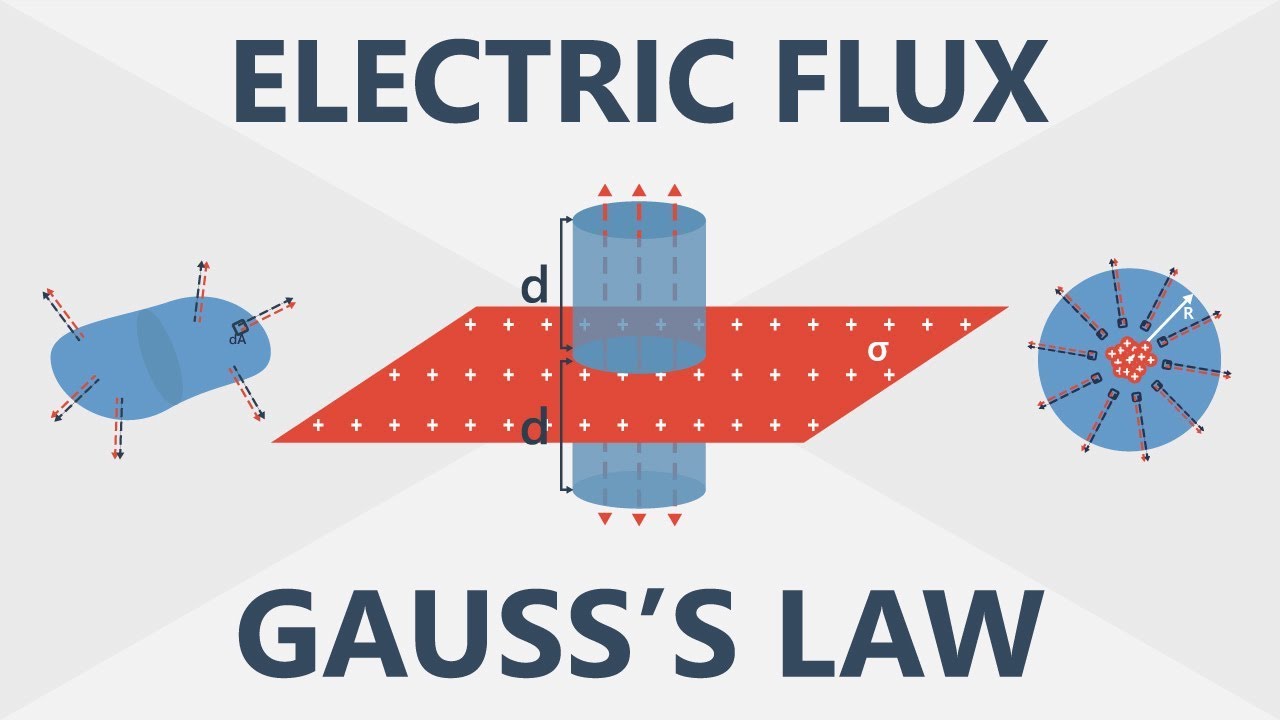
Electric Flux and Gauss’s Law | Electronics Basics #6

Area vector with examples & flux vector equation | Electric fields & charges | Khan Academy

Takeaways

Q & A

Why is area sometimes treated as a vector in physics?

What is the significance of treating area as a vector for the calculation of flux?

How is the direction of an area vector determined?

What is the relationship between the angle theta in the context of flux and the area vector?

Why is it difficult to standardize the direction of an area vector for open surfaces?

What is the advantage of using the dot product notation for calculating flux?

Can you give an example of how to calculate the flux through an area given the electric field and the angle?

What is the common mistake made when calculating the angle theta for flux calculations?

How does treating area as a vector help in the context of a closed surface?

What is the significance of the perpendicular component of the area in flux calculations?