Electric flux meaning (& how to calculate it) | Electrostatics | Physics | Khan Academy
TLDRThis video script delves into the concept of electric flux, a measure of electric field 'flow' through an area. It begins by comparing electric flux to water flow through a window, illustrating the basic principle of flux calculation. The script then transitions to the calculation of electric flux, emphasizing the importance of the angle between the electric field and the area. It explains how to generalize the concept for non-uniform fields and varying angles by dividing the area into infinitesimal pieces and integrating the flux over the entire surface. The video promises to derive the equation for electric flux from scratch, providing a foundational understanding that will later be applied to Gauss's Law, a powerful tool in electromagnetism.
Takeaways
- 📚 Electric flux is a concept that measures how much electric field is 'flowing' through a given area, even though nothing is actually flowing.
- 💡 The idea of electric flux helps us to understand Coulomb's inverse square law in a new light through Gauss's Law, which simplifies certain calculations.
- 🌊 To calculate electric flux, one can start by considering a similar concept with water flow, where water velocity is analogous to electric field strength.
- 🔍 The basic formula for calculating flux (e.g., water or electric) involves multiplying the field strength (or velocity) by the area through which it is 'flowing'.
- 📏 The units of electric flux are derived from the units of electric field strength (newtons per coulomb) and area (square meters), resulting in newton-meters squared per coulomb.
- 🧭 When the area is not perpendicular to the electric field, the calculation of flux must consider the component of the area that is perpendicular to the field.
- 📐 The effective area through which the electric field 'flows' can be found using trigonometry, especially when the area is tilted with respect to the field.
- ⚙️ For non-uniform electric fields or irregularly shaped areas, the flux is calculated by dividing the area into infinitesimally small pieces, calculating the flux for each, and then integrating these values.
- 📚 The most general equation for electric flux involves integrating the product of the electric field strength and the perpendicular component of the infinitesimal area (dA) over the entire surface.
- 🔄 The concept of flux is not limited to electric fields; it can be applied to any field, such as magnetic flux, by replacing the electric field strength with the magnetic field strength.
- 🔍 The script emphasizes the importance of understanding why we study certain concepts, like electric flux, and how they can be applied to solve complex problems in physics.
Q & A
What is the concept of electric flux?
-Electric flux is a measure of how much electric field is 'flowing' through a given area, even though there isn't any actual flow. It's an imagined concept to help visualize and calculate the effect of an electric field over a surface.
Why is electric flux important in understanding electric fields?
-Electric flux is important because it helps us to look at Coulomb's inverse square law in a different way, leading to Gauss's law, which simplifies the process of solving certain problems that would be tedious using Coulomb's law alone.
What is the basic formula for calculating electric flux?
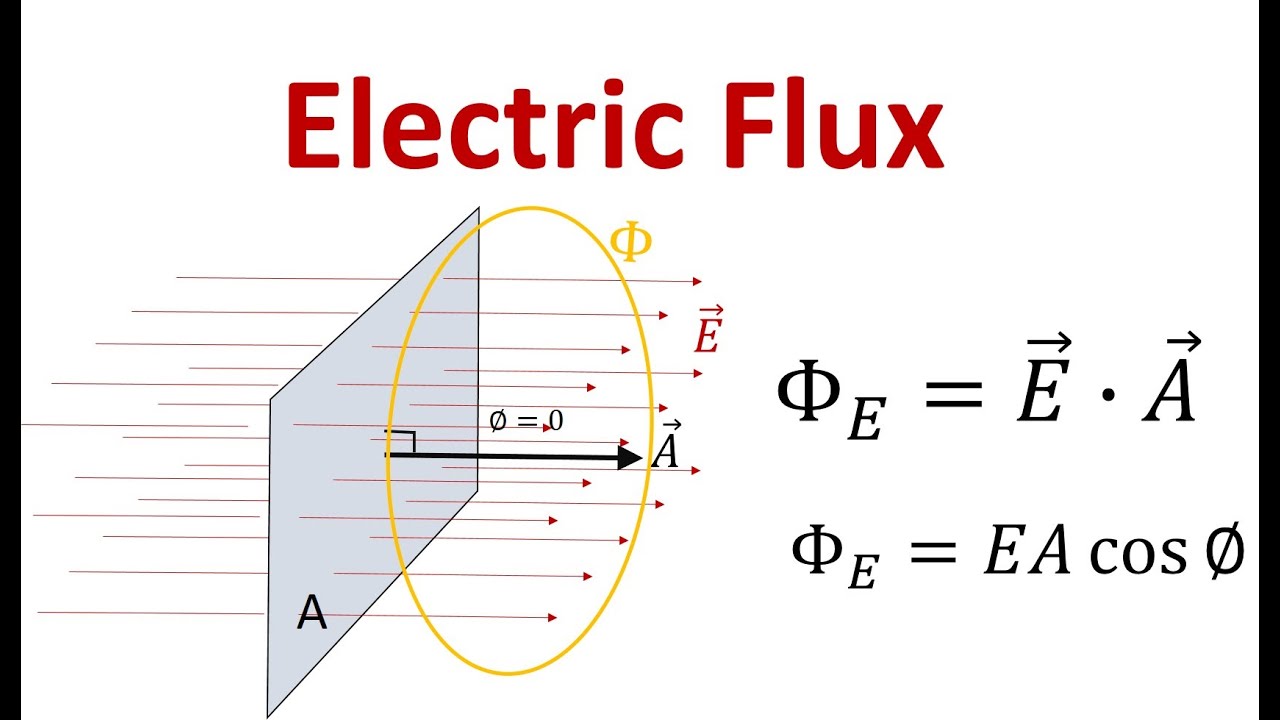
-The basic formula for calculating electric flux, denoted as phi (Φ), is the product of the electric field strength (E) and the area (A) perpendicular to the field, which can be represented as Φ = E * A⊥.
How does the orientation of an area relative to the electric field affect the electric flux?
-The orientation of an area affects the electric flux because the flux is calculated using the component of the area that is perpendicular to the electric field. If the area is tilted, the effective area through which the field 'flows' decreases, reducing the flux.
What is the unit of electric flux?
-The unit of electric flux is newton meter squared per coulomb (N·m²/C), which represents the amount of electric field 'flowing' through an area.
How can the concept of water flow be used to understand electric flux?
-The concept of water flow can be used as an analogy to understand electric flux. Just as the volume of water flowing through an area per second can be calculated by multiplying the velocity of the water by the area perpendicular to the flow, electric flux is calculated by multiplying the electric field strength by the perpendicular component of the area.
What happens to the electric flux when the area is parallel to the electric field?
-When the area is parallel to the electric field, the effective area through which the field 'flows' becomes zero, resulting in zero electric flux, because there is no component of the area perpendicular to the field.
How is electric flux calculated when the electric field is non-uniform?
-In the case of a non-uniform electric field, the area is divided into infinitesimally small pieces, each with a uniform field approximation. The flux is calculated for each small piece and then integrated over the entire area to find the total electric flux.
What is the most general equation for calculating electric flux?
-The most general equation for calculating electric flux is an integral over the surface: Φ = ∫E * dA⊥, where E is the electric field strength, dA⊥ is the perpendicular component of the infinitesimal area element, and the integral sums up the contributions from all such elements over the surface.
Can the concept of electric flux be applied to other types of fields?
-Yes, the concept of electric flux can be applied to other types of fields, such as magnetic fields. The formula for flux would be similar, with the electric field strength (E) replaced by the magnetic field strength (B), resulting in magnetic flux denoted as Φ_B.
Outlines
🔋 Understanding Electric Flux
This paragraph introduces the concept of electric flux, which is a measure of how much electric field is 'flowing' through a given area, even though it's not actually flowing. The video aims to derive the equation for electric flux from scratch and explains its importance in understanding Gauss's Law, which provides a new perspective on Coulomb's inverse square law. The analogy of water flow is used to explain the concept of flux, encouraging viewers to think about the units involved in calculating the flux of water through an area.
💧 Calculating Water Flux as an Analogy
The script uses the analogy of water flow to explain how to calculate flux. It describes a scenario where water is flowing to the right at a velocity of 10 meters per second and passes through a window with an area of 2 square meters. The goal is to calculate the volume of water flowing through the window per second, which is defined as the flux of water. The explanation involves visualizing a cube of water behind the window and calculating its volume after one second, which represents the flux. The units for this calculation are discussed, emphasizing the concept of volume per unit time.
📡 Transitioning from Water to Electric Flux
After establishing the concept of water flux, the script transitions to electric flux by replacing the water with an electric field. The strength of the electric field is likened to the velocity of water, leading to the formula for electric flux, which is the product of the electric field strength and the area through which it is considered to 'flow'. The units for electric flux are explained, and the importance of the angle between the electric field and the area is highlighted. The script then challenges the viewer to consider how the flux would change if the area were tilted, leading to a discussion of how to calculate flux in such a scenario.
📚 Generalizing Electric Flux Calculation
The script generalizes the calculation of electric flux by considering non-uniform electric fields and non-perpendicular areas. It explains that when the area is tilted, the effective area through which the electric field 'flows' is reduced, thus reducing the flux. The concept of 'a perpendicular' is introduced, which is the component of the area perpendicular to the electric field. The script then extends this to non-uniform fields by dividing the area into infinitesimally small pieces, calculating the flux over each piece, and integrating these to find the total flux. This approach is described as the most general method for calculating flux, applicable to any field, not just electric.
Mindmap
Keywords
💡Electric Flux
💡Electric Field
💡Area
💡Gauss's Law
💡Uniform Electric Field
💡Non-Uniform Electric Field
💡Perpendicular Component
💡Integration
💡Vector Form
💡Flow Analogy
Highlights
Introduction to the concept of electric flux, which is a measure of how much electric field is 'flowing' through an area.
The video aims to derive the equation for electric flux from scratch.
Explains the importance of studying electric flux in understanding Gauss's Law and its implications for electric fields.
An analogy is made between the flow of water and the concept of electric flux to aid understanding.
The formula for calculating the flux of water is introduced as a stepping stone to understanding electric flux.
The units of electric flux are discussed, relating to the units of electric field strength.
The generalization of the electric flux formula to account for non-perpendicular fields is explained.
Trigonometry is introduced as a method to calculate the effective area when the field is not perpendicular.
The concept of integrating over a surface to calculate electric flux in the case of non-uniform fields is introduced.
The integral form of the electric flux equation is presented as the most general form for calculating flux.
The video discusses the impact of the angle between the electric field and the area on the calculation of flux.
The idea of dividing the area into infinitesimally small pieces to assume uniformity for flux calculation is explained.
The concept of vector form for electric flux calculation is mentioned as a topic for a future video.
The video emphasizes the applicability of the flux concept to fields other than electric, such as magnetic flux.
The practical applications of understanding electric flux in solving complex problems using Gauss's Law are highlighted.
The video concludes with a summary of the key points about electric flux and its calculation methods.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: