Understanding How Torque Works
TLDRThe video script delves into the concept of torque, a fundamental principle in physics that describes the turning effect of forces on a rigid body. It explains that torque, also known as the moment of force, is calculated by multiplying the force applied by the perpendicular distance from the axis of rotation, measured in Newton meters (Nm). The script illustrates the principle of torque with a practical example of a beam balance, showing how the mass of an unknown object can be determined by comparing the torque created by the object to that of known calibration weights. The video also touches on the conditions of equilibrium, where an object remains stationary with a net force and moment of zero. This summary encapsulates the essence of the script, providing viewers with a clear understanding of torque and its applications.
Takeaways
- 🔧 **Torque Definition**: Torque is the turning effect of a force and is also known as the moment of force (τ).
- 🚪 **Door Handle Effort**: More effort is required to pull a door handle near the hinge due to the relationship between force magnitude and the perpendicular distance from the pivot (hinge).
- 📐 **Rigid Body Motion**: The door, as a rigid body, turns when all particles move angularly about an axis of rotation.
- ⚖️ **Torque Calculation**: Torque (τ) is calculated as the product of the force (F) and the perpendicular distance (d) from the hinge, expressed as τ = F x d.
- 📏 **Units of Torque**: The SI unit for torque is Newton metre (Nm), resulting from multiplying force in Newtons by distance in metres.
- 🧭 **Directionality**: Torque is a vector quantity, which means it has both magnitude and direction.
- 🔄 **Principle of Torque**: The principle of torque, or moment, states that for a body in equilibrium, the sum of clockwise moments equals the sum of anti-clockwise moments about the same pivot.
- ⚖️ **Beam Balance Example**: A beam balance with equal arms uses the principle of torque to balance known calibration weights against an unknown mass.
- ⚖️ **Mass Calculation**: By applying the principle of moment, the mass of an object (e.g., oranges) can be calculated using the formula involving weight, acceleration due to gravity, and perpendicular distance from the pivot.
- 🔍 **Conditions of Equilibrium**: An object is in equilibrium when it is stationary with zero resultant force and moment acting on it.
- ⚙️ **Resultant Force and Moment**: When an object does not rotate, the clockwise and anti-clockwise moments acting on it are balanced, resulting in zero resultant moment.
Q & A
What is torque?
-Torque, also known as the moment of force, is a measure of the turning effect of a force. It is calculated as the product of the force magnitude and the perpendicular distance from the axis of rotation (hinge), expressed in Newton metres (Nm). Torque is a vector quantity that depends on both the magnitude and direction of the force.
Why is more effort required to pull a door handle near the hinge?
-More effort is required to pull a door handle near the hinge because the perpendicular distance (d) from the hinge is smaller, resulting in a lower torque according to the formula τ = F x d. To achieve the same turning effect, a greater force (F) must be applied.
What is the principle of torque?
-The principle of torque, also known as the principle of moment, states that when a body is in equilibrium, the sum of the clockwise moments about a pivot is equal to the sum of the anti-clockwise moments about the same pivot.
How does the principle of moment apply to a beam balance?
-The principle of moment applies to a beam balance by ensuring that the clockwise moment (force times distance from the pivot) of the calibration weights is equal to the anti-clockwise moment of the objects being weighed. This allows for the balance to remain horizontal and for the mass of the objects to be determined.
How can you calculate the unknown mass of the oranges using the principle of moment on a beam balance?
-By applying the principle of moment, you can equate the torque of the oranges (mass of oranges times acceleration due to gravity times distance from pivot) to the torque of the calibration weights (mass of calibration weights times acceleration due to gravity times distance from pivot). If the mass of the calibration weights is known, you can solve for the mass of the oranges.
What is the SI unit of torque?
-The SI unit of torque is the Newton metre (Nm), which is the product of the force in Newtons and the perpendicular distance from the axis of rotation in metres.
What is the relationship between weight and force?
-Weight is the force of gravity acting on an object. It can be calculated as the product of the object's mass and the acceleration due to gravity (weight = mass x acceleration due to gravity).
What conditions must be met for an object to be in equilibrium?
-For an object to be in equilibrium, the resultant force acting on it must be zero, meaning all forces cancel each other out. Additionally, the resultant moment (torque) acting on it must also be zero, indicating that the clockwise and anti-clockwise moments are balanced.
How does the axis of rotation affect the turning effect on a rigid body?
-The axis of rotation is the line about which all particles of a rigid body move angularly when a turning effect occurs. The axis of rotation, in conjunction with the applied force and the perpendicular distance from the force to the axis, determines the turning effect on the body.
What is the formula for torque?
-The formula for torque (τ) is τ = F x d, where F is the force applied, measured in Newtons, and d is the perpendicular distance from the axis of rotation (or hinge), measured in metres.
Why is torque a vector quantity?
-Torque is a vector quantity because it has both magnitude and direction. The direction of the torque is determined by the direction of the force and the axis of rotation, which can result in a turning effect that is clockwise or anti-clockwise.
How does the principle of torque relate to the conditions of equilibrium?
-The principle of torque is closely related to the conditions of equilibrium because it dictates that for an object to remain stationary (not rotate), the sum of the clockwise torques must equal the sum of the anti-clockwise torques about any given pivot point. This balance of torques ensures that the object does not experience a net turning effect.
Outlines
🔧 Understanding Torque and its Principles
This paragraph introduces the concept of torque, which is the turning effect of forces on a rigid body, such as a door. It explains that torque depends on the magnitude of the force and the perpendicular distance of the force from the axis of rotation, typically a hinge. The formula for torque is given as torque (τ) equals force (F) times distance (d), measured in Newton metres (Nm). The principle of torque, also known as the principle of moment, is discussed, stating that for a body in equilibrium, the sum of clockwise moments equals the sum of anti-clockwise moments about a pivot. An example of a beam balance is used to illustrate this principle, where the mass of an unknown object can be calculated by comparing it to known calibration weights. The conditions of equilibrium are also covered, stating that a stationary object has a resultant force and moment of zero.
Mindmap
Keywords
💡Torque
💡Rigid Body
💡Axis of Rotation
💡Magnitude of Pull
💡Perpendicular Distance
💡Newton Metre (Nm)
💡Vector Quantity
💡Principle of Torque
💡Beam Balance
💡Calibration Weights
💡Conditions of Equilibrium
Highlights
Torque is the turning effect of forces on a rigid body
Torque depends on the magnitude of the force and the perpendicular distance from the hinge
Torque is calculated as F x d, where F is force in Newtons and d is distance in meters
The SI unit of torque is Newton meter (Nm)
Torque is a vector quantity that depends on both magnitude and direction
The principle of torque states that the sum of clockwise and anti-clockwise moments on a pivot must be equal for equilibrium
A beam balance demonstrates the principle of torque, with equal distances from the pans to the pivot
The mass of the oranges can be calculated using the principle of moment and torque formula
Weight is a force that can be substituted into the torque formula as mass times acceleration of gravity
When the beam is balanced, the mass of the oranges equals the total mass of the 3 calibration weights
An object in equilibrium has zero resultant force and moment acting on it
Torque plays a key role in understanding the effort required to pull a door handle
The door acts as a rigid body that does not deform under the applied forces
The axis of rotation is the line where all centers of the particles moving angularly lie
The torque formula can be rearranged to solve for unknown variables like mass
The equal arm balance demonstrates the principle of torque with equal distances and moments
The torque concept can be applied to real-world scenarios like finding the mass of objects
Understanding torque helps explain everyday phenomena like the effort needed to open a door
Transcripts
Browse More Related Video

What is Torque? | Physics | Extraclass.com
Moments, Torque, Toppling & Couples - GCSE & A-level Physics (full version)
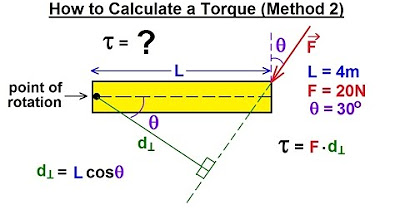
Physics 15 Torque Fundamentals (5 of 13) How to Calculate a Torque (Method 2)
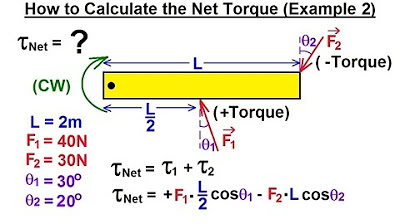
Physics 15 Torque Fundamentals (11 of 13) How to Calculate the Net Torque? Ex. 2
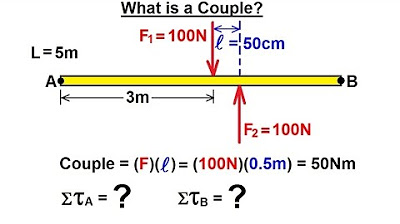
Physics 15 Torque (6 of 27) What is a Couple?

torque explained
5.0 / 5 (0 votes)
Thanks for rating: