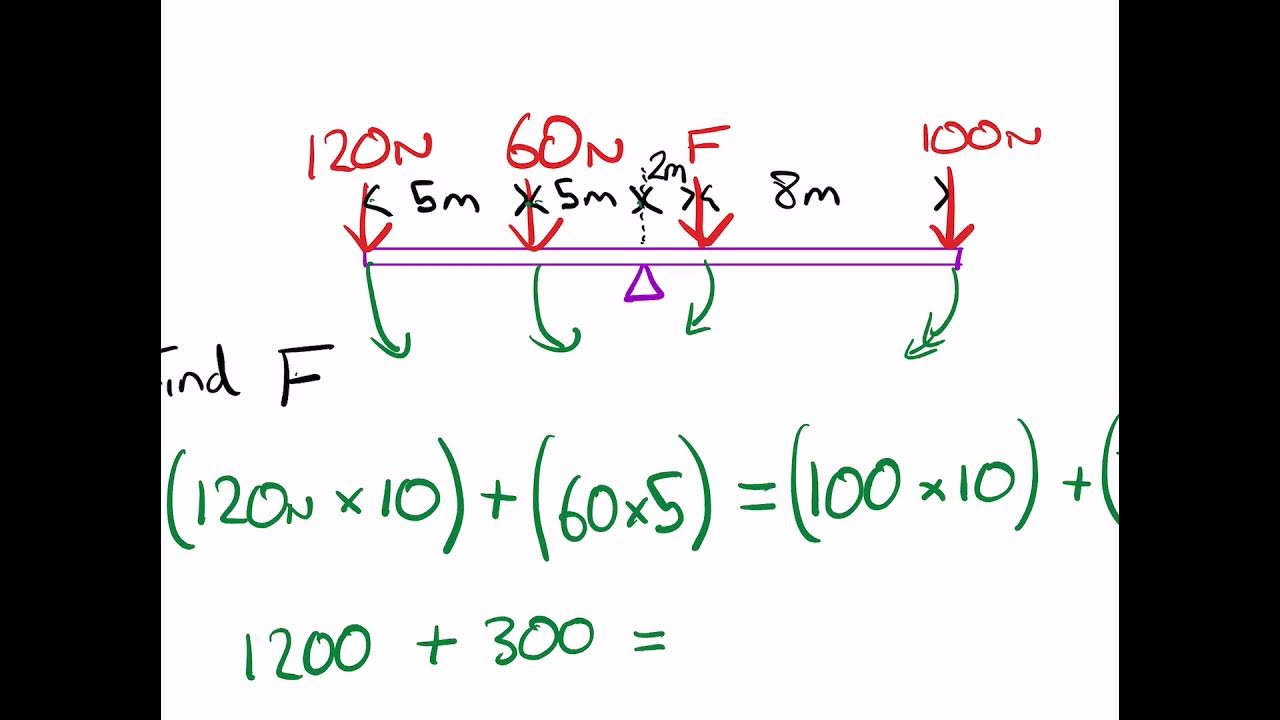Moments, Torque, Toppling & Couples - GCSE & A-level Physics (full version)
TLDRThis video script delves into the concept of moments, also known as torque, in physics. It explains how force applied at a distance from a pivot point creates a moment that can cause rotation. The importance of the perpendicular distance from the pivot and the force's line of action is highlighted. Practical examples, such as a seesaw and a lighting rig, illustrate the principle of moments for equilibrium, where the sum of anti-clockwise moments equals the sum of clockwise moments. The script also touches on calculating moments in systems with forces at angles, using trigonometric functions to resolve the force into components perpendicular to the pivot. It addresses the concept of toppling, where an object will fall if its center of mass shifts past the pivot point. Lastly, the video introduces the idea of couples, where two equal and opposite forces create a net moment if applied at different distances from the pivot. The summary aims to provide a clear understanding of moments and their role in equilibrium and rotation, emphasizing the need for practice to master these mechanical concepts.
Takeaways
- 🔧 A moment is a force applied to an object times the distance from the pivot, perpendicular to the force's line of action.
- 🌀 Moment, also known as turning force or torque, is measured in newton meters (Nm).
- ⚖️ For equilibrium, the sum of the anti-clockwise moments must equal the sum of the clockwise moments.
- 🤔 When finding unknowns, it can be helpful to choose one of them as the pivot to simplify the equation.
- 📐 The weight of an object, such as a beam, is often considered to be at the center for simplicity.
- 🔄 In a system in equilibrium, the sum of the clockwise moments equals the sum of the anti-clockwise moments, and there's no resultant force.
- 📍 When calculating moments with forces at an angle, use the force times the perpendicular distance from the pivot times the cosine of the angle.
- 🤾♀️ In a roundabout scenario, forces acting perpendicular to each other (90 degrees) still follow the principle of moments for equilibrium.
- 🏋️♂️ Toppling occurs when the center of mass of an object passes the pivot point, causing a moment that turns the object clockwise.
- 🚗 The moment of a couple (two equal and opposite forces) is defined as one of the forces times the distance between the forces.
- 📚 Practice is key to mastering the calculation and application of moments in various mechanical scenarios.
Q & A
What is the physical principle that describes how force and distance from a pivot affect rotation?
-The physical principle that describes this is called the moment, which is the product of the force applied and the perpendicular distance from the pivot to the line of action of the force.
What are the units used to measure moments?
-Moments are measured in newton meters (Nm), which is the product of force in newtons and distance in meters.
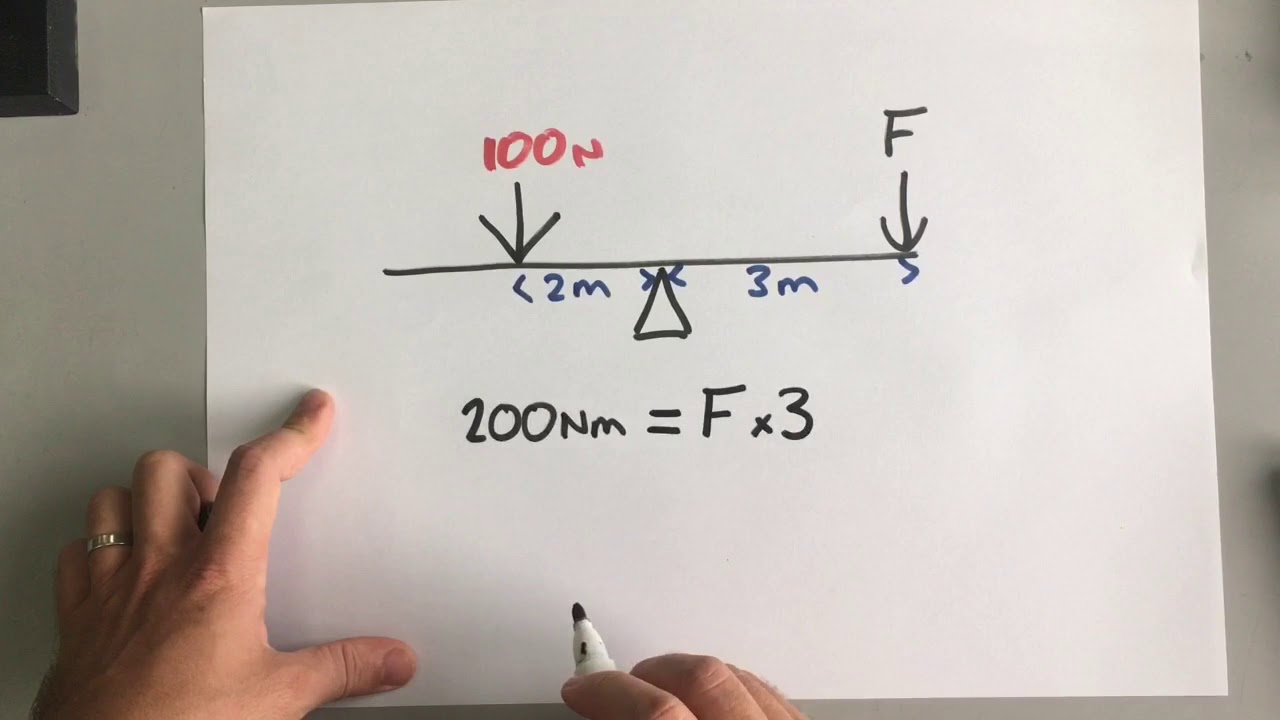
How do you calculate the moment of a weight on a seesaw?
-The moment is calculated by multiplying the force (weight) in newtons by the distance from the pivot in meters.
What is the principle of moments for an object to be in equilibrium?
-For an object to be in equilibrium, the sum of the anti-clockwise moments must equal the sum of the clockwise moments.
How do you find the tension in a cable supporting a weight if there is no obvious pivot?
-You can choose any point as a pivot and apply the principle of moments to create an equation that relates the moments due to the forces acting on the system.
What is the formula to calculate the moment of a force acting at an angle?
-The moment of a force acting at an angle is calculated as the force times the perpendicular distance from the pivot to the line of action of the force, often represented as F times d times cos(theta) or F times d times sin(theta), depending on the orientation.
What is the condition for a roundabout to be in equilibrium when forces are acting perpendicular to each other?
-The condition for equilibrium is that the sum of the moments of all forces acting in one direction (e.g., anti-clockwise) must equal the sum of the moments of all forces acting in the opposite direction (e.g., clockwise).
What is the concept of toppling in the context of moments?
-Toppling occurs when the center of mass of an object moves past the pivot point, causing the object to rotate and fall due to the unbalanced moment created.
How is the moment of a couple defined?
-The moment of a couple is defined as one of the forces times the distance between the forces, which results in twice the product of the force and the radius for a couple acting on a pivot.
What is the significance of the direction of forces when calculating moments?
-The direction of forces is crucial as it determines whether the moment will act clockwise or anti-clockwise, which is essential for calculating the net moment and assessing equilibrium.
Why is it important to consider the perpendicular distance from the pivot when calculating moments?
-Considering the perpendicular distance is important because it is the shortest distance from the pivot to the line of action of the force, which directly affects the magnitude of the moment.
How can you find the tension in a system with multiple unknowns, such as a lighting rig supported by two cables?
-You can find the tension by setting up equations based on the equilibrium conditions, which state that the sum of the clockwise moments equals the sum of the anti-clockwise moments and the sum of the upward forces equals the sum of the downward forces.
Outlines
🔧 Understanding Moments and Equilibrium
The first paragraph introduces the concept of moments, also known as turning force or torque, which is the product of the force applied and the perpendicular distance from the pivot. It explains that the direction of the force is crucial and that for an object to be in equilibrium, the sum of the anti-clockwise moments must equal the sum of the clockwise moments. This principle is illustrated with the example of a seesaw, showing how to calculate the moment for different weights at various distances from the pivot. The paragraph also touches on the idea of balancing moments in more complex systems, such as a lighting rig supported by cables.
📐 Calculating Moments with Angles and Forces
The second paragraph delves into calculating moments when forces are applied at angles, using the example of a shelf supported by a wire. It explains that the moment is equal to the force times the perpendicular distance from the pivot to the force's line of action. The concept of resolving forces into components perpendicular to the beam is introduced, and the use of trigonometric functions (cosine or sine) is shown to calculate the moment due to a force at an angle. The paragraph also discusses the equilibrium conditions in more complex scenarios, such as a roundabout with people pushing in opposite directions, and the prevention of toppling by ensuring the center of mass does not pass the pivot point.
🤸♂️ Couples and the Definition of Moments
The third paragraph discusses the concept of couples, which are pairs of forces that produce equal and opposite moments about a pivot, resulting in no net movement. Using the example of a steering wheel, it clarifies that the moments due to each hand's force are added to find the total moment of the couple. The distinction is made between the total moment and the definition of a couple's moment, which is the force times the distance between the forces. The paragraph emphasizes the importance of understanding moments for equilibrium and the prevention of toppling in mechanical systems.
Mindmap
Keywords
💡Force
💡Pivot
💡Moment (Torque)
💡Distance from Pivot
💡Units (Newton Meters)
💡Equilibrium
💡Resultant Force
💡Lighting Rig
💡Couple
💡Toppling
💡Angles and Directions
Highlights
A moment is the force applied to an object times the distance from the pivot, with the force being perpendicular to the line of action.
Moments are measured in newton meters and are also known as turning force or torque.
To find the moment, consider the direction (clockwise or anti-clockwise) the force is pulling.
For equilibrium, the sum of anti-clockwise moments must equal the sum of clockwise moments.
In a system like a lighting rig, you can choose any point as the pivot to calculate moments.
When finding unknowns, make one of them the pivot to simplify the equation.
For equilibrium, the sum of all downward forces must equal the sum of all upward forces.
When forces are at different angles, find the component of the force perpendicular to the pivot to calculate the moment.
Use the cosine of the angle between the force and the beam to find the perpendicular component of the force.
In a roundabout, the perpendicular distances from the force to the pivot determine the direction (clockwise/anti-clockwise) of the moment.
Toppling occurs when the center of mass passes the pivot point and the moment causes clockwise rotation.
The moment of a couple (two equal, opposite forces) is the force times the distance between the forces.
Systems are not always in equilibrium - moments are equal only when the system is in equilibrium.
Practice solving problems involving moments to get good at mechanics.
Different angles and directions of forces can complicate moment calculations but can be simplified with practice.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: