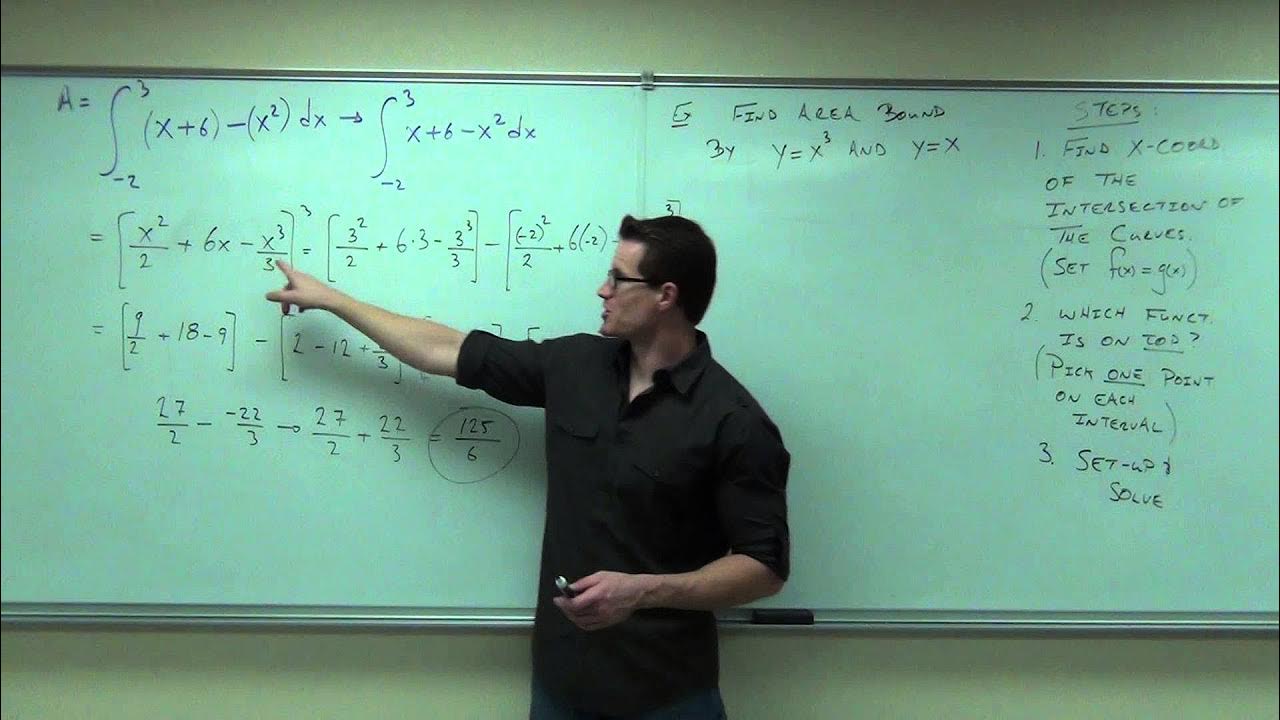4.4 - Properties of Definite Integrals
TLDRThe video script delves into the concept of definite integrals and their application in calculating areas under curves, specifically focusing on the additive property of integrals. This property allows for the integration of more complex functions by splitting them into simpler parts based on different rules or 'pieces' within their domain. The video explains how to handle piecewise functions and absolute value functions by breaking them down at points where the function's rule changes. It also explores the calculation of areas between two curves, emphasizing the importance of determining the upper and lower functions and their points of intersection. The script further illustrates how to find the average value of a function over an interval, treating it as the accumulation of y-values divided by the width of the interval. Practical examples, including calculating the average weekly sales of an online business, are provided to demonstrate the application of these mathematical concepts in real-world scenarios.
Takeaways
- 📐 The additive property of definite integrals allows for the integration of functions that have different rules across various parts of their domain by splitting the integral at an intermediate value.
- 📈 To find the area under a curve of a piecewise function, one can evaluate separate definite integrals for each section of the function and sum the results.
- 🔢 The process involves finding anti-derivatives for each section of the function, evaluating these at the respective limits of integration, and combining the results according to the rules of addition and subtraction.
- 🏞️ The concept of definite integrals can be extended to calculate more complex areas, such as those bounded by two curves, by finding the difference between the integrals of the upper and lower functions.
- 🤝 The order of functions as upper or lower is crucial when calculating the area between two curves, as it directly impacts the sign of the resulting integral.
- 🤔 To determine the upper and lower functions, one can use a test value within the integration range and compare the outputs of the two functions to see which is greater.
- 📉 The issue of negative area can arise when the orientation of the graphs changes within the integration interval, but this can be addressed by breaking the integral into parts where the orientation remains consistent.
- 🧮 Definite integrals are not only used for geometric area calculations but also to find the average value of a function over an interval, which is done by dividing the integral by the width of the interval.
- 💡 The average value of a function can provide meaningful insights in applied contexts, such as estimating average weekly sales for a business based on a given function of sales over time.
- 🚧 When dealing with functions that intersect the x-axis, it's important to consider the x-axis as a function (g(x) = 0) to properly calculate areas and avoid issues with negative values.
- 🔠 For more complex functions or those that require integration by parts, special strategies and techniques will be needed, which will be the focus of subsequent discussions.
Q & A
What is the additive property of definite integrals?
-The additive property of definite integrals allows us to split the integral of a function that has different rules for different parts of its domain. By using an intermediate value within the limits of integration, we can evaluate the integral in segments and then sum those segments to find the total integral.
How does the additive property of integrals apply to piecewise functions?
-The additive property is particularly useful for piecewise functions, which have more than one function rule that applies to different values of x. By using an intermediate x value where the function rule changes, we can split the integral and integrate each part separately, then sum the results to get the total integral over the entire domain.
What is the process for evaluating the definite integral of a function with two different rules over an interval from negative 3 to 6?
-First, identify the intermediate value where the function's rule changes, which is x=2 in the given example. Then, split the integral into two parts: from the lower limit (negative 3) to the intermediate value (2) and from the intermediate value (2) to the upper limit (6). Integrate each part separately using the appropriate function rule for each interval and sum the results to find the total area under the curve.
How can we find the area under the graph of a function that is defined piecewise?
-To find the area under a piecewise function, you need to calculate the definite integral of each piece of the function over the respective intervals where the piece is defined. Then sum these areas together to get the total area under the graph of the entire piecewise function.
What is the strategy for evaluating the integral of an absolute value function?
-For an absolute value function, you first define the function in piecewise terms, where the function changes depending on whether the input value is non-negative or negative. Then, you find the points where the function changes behavior (usually at zero or another critical point). You then split the integral at these points and evaluate each segment separately, summing the results to get the total integral.
How do you determine the area between two curves using definite integrals?
-To find the area between two curves, you first determine the points of intersection of the two curves, which will serve as the limits of integration. Then, you identify which curve is the upper function and which is the lower function over the interval of interest. The area between the curves is given by the integral of the upper function minus the integral of the lower function over the interval.
What is the general procedure for finding the area between two curves?
-The general procedure involves: (1) finding the points of intersection of the two curves to determine the limits of integration, (2) determining which curve is the upper function and which is the lower function over the interval, (3) setting up the integral of the upper function minus the lower function over the interval, and (4) evaluating the integral to find the area.
How can you handle a situation where the orientation of two graphs changes within the interval of integration?
-In such a situation, you split the integral into parts based on where the orientation changes. You calculate separate definite integrals for each part, taking care to correctly identify the upper and lower functions for each subinterval, and then sum these integrals to get the total area.
What is the average value of a function over an interval, and how do you calculate it?
-The average value of a function over an interval is the total accumulated value of the function's y-values over the interval, divided by the length of the interval. It is calculated by evaluating the definite integral of the function over the interval and then dividing by the difference between the upper and lower limits of the interval.
How can you use definite integrals to find the average weekly sales over a certain number of weeks for a business?
-You would use the function that models the weekly sales as a function of time, set the limits of integration to cover the weeks in question, calculate the definite integral of the sales function over that interval, and then divide by the number of weeks to find the average weekly sales.
What if the function to be integrated is more complicated, such as a product of functions or a composition of functions?
-For more complicated functions, there isn't always a simple rule or formula for integration. Advanced techniques such as integration by parts, substitution, or using tables of integrals may be required. These methods are typically introduced in more advanced calculus courses.
Outlines
📚 Introduction to Definite Integrals and Additive Property
This paragraph introduces the concept of definite integrals and discusses an additional property that allows for the integration of more complex functions. It explains how to handle functions with different rules over various parts of their domain by splitting the integral at an intermediate value within the limits of integration. This property is particularly useful for integrating piecewise functions, which have multiple rules that apply to different ranges of x-values. An example is provided to illustrate the process of finding the area under the curve of a function with two distinct rules by integrating separately over each rule's range and summing the results.
🔢 Evaluating Definite Integrals and Anti-derivatives
The paragraph delves into the process of evaluating definite integrals by finding anti-derivatives and applying them to specific intervals. It demonstrates how to integrate a function defined by two different rules over separate intervals and then combine these to find the total area under the curve. The example involves integrating from negative three to two and then from two to six, evaluating the anti-derivatives at the respective limits, and combining the results to find the total area, which is shown to be 83/3 square units.
📈 Integrating Absolute Value Functions and Piecewise Definitions
This section explores the integration of absolute value functions and how the additive rule for integrals can be applied to these. The absolute value is defined piecewise, either as the number itself for non-negative inputs or as the negation of the number for negative inputs. An example is given for integrating the absolute value of (x - 3) from 0 to 4, which requires splitting the integral at x = 3 and simplifying the expression before integrating. The final area under the curve is calculated to be 5 square units.
🏞️ Finding Areas Between Two Curves Using Definite Integrals
The paragraph explains how to find the area enclosed between two curves using definite integrals. It introduces the concept of an upper and lower function and demonstrates how to calculate the area between them as the difference of their respective areas from a to b. The importance of identifying the correct upper and lower functions and their intersection points is emphasized. A general procedure for finding the area between two curves is outlined, which includes determining the points of intersection and the limits of integration.
🤔 Determining Upper and Lower Functions for Area Calculation
This paragraph discusses methods for determining which function is the upper and which is the lower when finding the area between two curves. It suggests using a graphing calculator or a test value within the integration range to ascertain the functions' relative positions. An example is provided with two functions, f(x) and g(x), where the points of intersection are found algebraically and graphically, and the functions' roles as upper or lower are determined accordingly.
🧮 Calculating the Area Between Curves with Algebraic Methods
The paragraph focuses on algebraic techniques to find the points of intersection and to determine the upper and lower functions for calculating the area between curves. It shows how to set the functions equal to each other to find the x-values of intersection and how to choose a test value within the integration range to identify the upper function. The process is illustrated with an example where the functions are integrated from 0 to 2, and the area enclosed by the curves is calculated to be 4/3 square units.
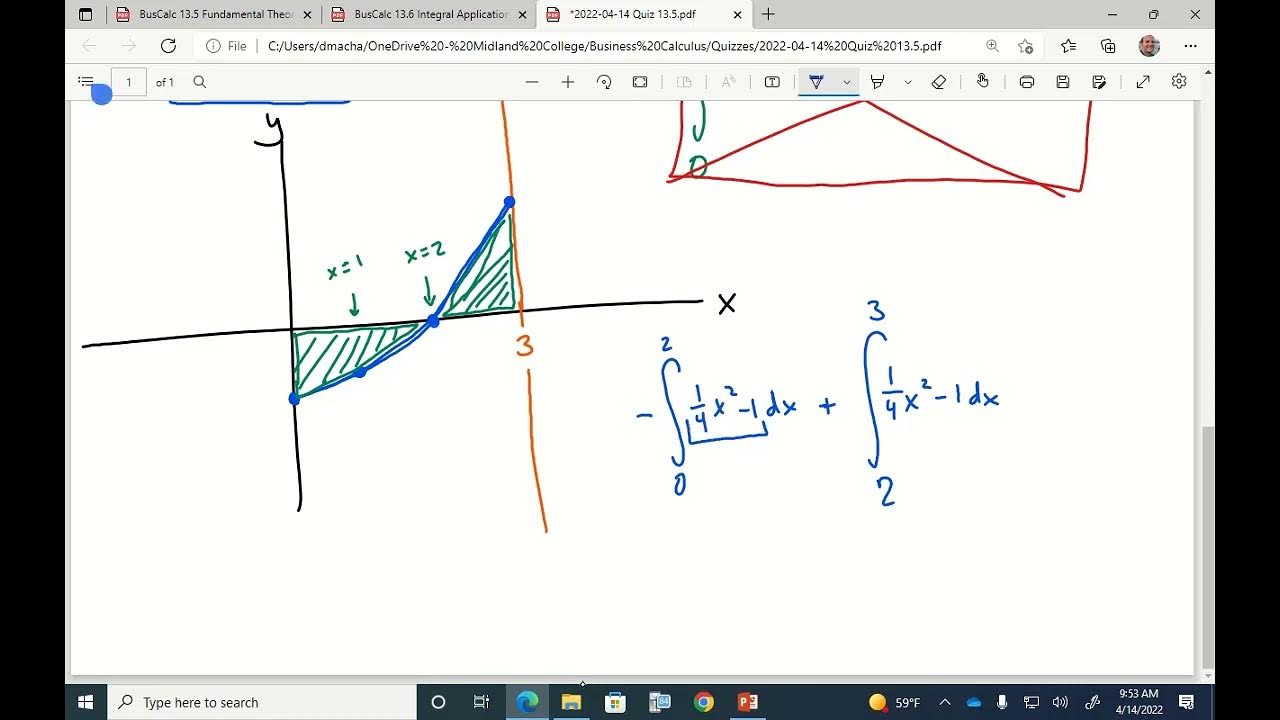
📉 Handling Multiple Intersections and Negative Areas
This section addresses the scenario where two functions intersect at more than two points, leading to changes in the orientation of the graphs and the need to calculate the area in segments. The concept of negative area is introduced, and a strategy is presented for dealing with it by splitting the integral into parts that account for the changes in the upper and lower functions. An example demonstrates how to calculate the total area by summing the areas calculated over different intervals defined by the points of intersection.
🧩 Breaking Down Complex Areas into Simpler Parts
The paragraph explains how to approach calculating the area when the orientation of the graphs changes within the interval of integration. It suggests breaking down the area into parts where the upper and lower functions can be consistently defined. This approach involves writing separate definite integrals for each part and then summing these to find the total area. The example provided involves integrating from negative five to three, with changes in the upper and lower functions at negative one, resulting in two separate integrals that are summed for the total area.
💡 Strategy for Dealing with Negative Areas in Integration
This part of the script discusses a method for addressing negative areas that may arise when integrating functions that cross the x-axis. It proposes treating the x-axis as a second function and adjusting the integral to ensure that all areas are considered as positive. The strategy involves breaking down the integral into segments based on the points where the function crosses the x-axis and then integrating each segment with the appropriate function as the upper or lower function. This approach ensures that the total area is calculated as a sum of positive values.
🎯 Average Value of a Function and Its Application
The paragraph introduces the concept of using definite integrals to find the average value of a function over an interval. It explains that the average value can be found by dividing the definite integral of the function by the width of the interval. An example is provided to illustrate the calculation of the average value of a function from 0 to 2. The concept is then applied to a real-world scenario where the average weekly sales of an online business are calculated for the first five weeks of operation using the definite integral of the sales function over the given interval.
📊 Calculating Average Sales Over a Specific Range
This section demonstrates how to calculate the average weekly sales for a specific range of weeks, in this case, from week two to week five, using definite integrals. It clarifies the limits of integration, which start at one week (t=1) instead of zero, and end at five weeks (t=5). The calculation involves integrating the sales function from one to five and then adjusting the result to reflect the actual dollar amount in hundreds of dollars. The final step is to convert the result into an approximate dollar amount, providing a meaningful average weekly sales figure for the specified period.
🔧 Recap and Preview of Upcoming Integration Topics
The final paragraph recaps the topics covered in the discussion about area and integration, including Riemann sums, definite integrals, and strategies for finding areas between curves. It highlights the complexity of integration compared to differentiation and notes that while there are standard rules for many functions, there isn't always a definitive formula for more complicated functions. The paragraph previews upcoming topics that will explore strategies for integrating more complex functions, such as products of functions, nested functions, and compositions.
Mindmap
Keywords
💡Definite Integrals
💡Additive Property of Integrals
💡Piecewise Function
💡Anti-derivatives
💡Area Under a Curve
💡Integration by Parts
💡Average Value of a Function
💡Natural Logarithm
💡Exponential Functions
💡Riemann Sum
💡Integration Strategies
Highlights
The video discusses the additive property of definite integrals, which allows for the integration of functions with different rules across various parts of their domain.
Introduces the concept of splitting a definite integral using an intermediate value within the limits of integration to handle piecewise functions.
Demonstrates how to evaluate the area under the curve of a function with two different rules by splitting the integral at the point where the function rule changes.
Provides an example of integrating a function from -3 to 6, showcasing the process of splitting the integral at an intermediate value and summing the results.
Explains the application of the additive property of integrals to absolute value functions, which can be defined piecewise.
Illustrates the process of evaluating a more complex absolute value function by defining piecewise rules and splitting the integral accordingly.
Discusses calculating the area between two curves, which involves finding the difference between the integrals of the upper and lower functions.
Details a general procedure for finding the area between two curves, including determining points of intersection and identifying the upper and lower functions.
Presents a method for algebraically determining the points of intersection of two functions by setting them equal to each other and solving for x.
Shows how to handle situations where the orientation of the graphs (upper and lower functions) changes within the interval of integration by splitting the integral.
Provides an example of calculating the area between curves with changing orientations and how to apply the additive property of integrals in such cases.
Introduces the concept of using definite integrals to find the average value of a function over an interval, extending the idea beyond geometric applications.
Demonstrates how to calculate the average value of a function by integrating over an interval and dividing by the length of the interval.
Applies the concept of average value to a real-world scenario, calculating the average weekly sales of an online business over a five-week period.
Explains the significance of the average value in understanding the average performance over a span of time, rather than at specific discrete points.
Discusses the limitations and challenges of integration compared to differentiation and introduces the topic of more complex integration strategies for future lessons.
Highlights the importance of understanding the fundamental properties of integrals, such as additivity, to tackle more complicated functions and applications.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: