Definite Integrals from Graphs (Part 3 of 3) - Absolute Value

turksvids
3 Dec 201709:25
EducationalLearning
32 Likes 10 Comments

TLDRThis video script discusses the concept of finding definite integrals from graphs, focusing on the intricacies involved when dealing with absolute value functions. The presenter emphasizes that the absolute value of a function, F(x), results in an even function, which simplifies the graph to only the positive part reflected over the y-axis. This property is crucial for calculating definite integrals. The video outlines three scenarios where absolute values appear in integrals: taking the absolute value of the integral, integrating the absolute value of the function, and integrating the function of the absolute value of x. Each case is illustrated with examples, demonstrating how to handle negative areas by reflecting parts of the graph over the x-axis to convert them into positive regions. The presenter also addresses the common case of symmetric bounds and how to leverage the even function property to simplify calculations. The script provides a comprehensive guide to understanding and solving integrals involving absolute values, offering viewers a clear and engaging explanation of the process.

Takeaways
  • 📊 **Even Function Property**: The function F of the absolute value of X is an even function, meaning F(-X) = F(X), which is crucial for graphing and calculating integrals.
  • 🚫 **Graph Discrimination**: When graphing F of the absolute value of X, discard the graph for X less than zero and reflect the remaining graph over the y-axis to achieve symmetry.
  • ➕ **Positive Integrals**: The absolute value of a definite integral will always result in a positive number, regardless of the original integral's sign.
  • 🔄 **Signed Area Transformation**: The absolute value of F(X) reflects negative areas above the x-axis, converting them into positive regions.
  • 📐 **Graph Reflection for Integrals**: For integrals involving F of the absolute value of X, reflect the negative part of the graph over the x-axis to find the corresponding positive area.
  • 🔢 **Direct Calculation**: Sometimes, it's more efficient to calculate the integral directly from the right-hand side of the graph, using symmetry properties.
  • ⛓ **Chain of Integral Cases**: There are three main cases for dealing with absolute values in integrals: absolute value of the integral, integral of the absolute value of the function, and integral of F of the absolute value of X.
  • 🔲 **Symmetry in Even Functions**: For even functions, integrals from negative to positive bounds can be calculated as twice the integral from zero to the positive bound.
  • 📈 **Signed Area Calculation**: When the function is below the x-axis, reflect the area above the x-axis to calculate the integral of the absolute value of the function.
  • 🔍 **Key Point Reflection**: Identify key points on the graph, reflect them according to the function's even properties, and connect them to find the required area.
  • 🛠️ **Calculator Aids**: For complex integrals, using a calculator can simplify the process, especially when dealing with difficult y-intercepts or complex areas.
Q & A

  • What is a key property of the function F of the absolute value of X?

    -The key property is that F of the absolute value of X is an even function. This is because F(-x) equals F(|x|), which is the same as F(x), fulfilling the definition of an even function.

  • How does the graph of an even function relate to the graph of F of the absolute value of X?

    -The graph of an even function is symmetric about the y-axis. For F of the absolute value of X, you discard the graph for x less than zero and reflect the remaining graph over the y-axis to create a symmetric graph.

  • What does the absolute value of a definite integral represent?

    -The absolute value of a definite integral represents the positive magnitude of the integral's result. If the result of the integral is negative, you take its absolute value to make it positive.

  • How does the integral of the absolute value of a function differ from a regular integral?

    -The integral of the absolute value of a function takes into account both the positive and negative areas under the curve, converting negative areas to positive by reflecting parts of the graph below the x-axis above it.

  • What is the significance of considering the integral from A to B of F of the absolute value of X DX?

    -This case is significant because it requires you to consider the even nature of the absolute value function and may involve reflecting parts of the graph to find the integral over a symmetric interval, which can be more complex than other cases.

  • How can you find the value of an integral with absolute value over a range where the function is below the x-axis?

    -You can reflect the part of the graph that is below the x-axis above the x-axis to convert negative areas to positive and then calculate the integral over the transformed graph.

  • What is a common approach to evaluating an integral with absolute value over a range that includes both positive and negative areas?

    -A common approach is to calculate the integral over the positive range and then add the absolute value of the integral over the negative range to find the total integral.

  • Why is it beneficial to consider the right-hand side of the graph when calculating definite integrals of even functions?

    -Considering the right-hand side of the graph is beneficial because the even nature of the function allows you to use symmetry to find the integral over the entire range by reflecting the right-hand side graph over the y-axis.

  • How can you use symmetry to simplify the calculation of an integral from a negative to a positive range for an even function?

    -You can use symmetry by calculating the integral from zero to the positive limit of the range and then multiplying the result by two, since the function's even nature means the integral from the negative to the positive range is twice the integral from zero to the positive limit.

  • What is the general strategy for finding the integral from a negative to a positive range of F of the absolute value of X DX when dealing with symmetric bounds?

    -The general strategy is to recognize the even function property, calculate the integral from zero to the positive limit, and then multiply by two to account for the symmetry, thus finding the integral over the entire range.

  • Why is it sometimes helpful to draw an even function like x squared when working with F of the absolute value of X?

    -Drawing an even function like x squared can help visualize the symmetry and transformations needed to calculate the integral of F of the absolute value of X, especially when dealing with complex or abstract functions.

Outlines
00:00
📊 Understanding Definite Integrals from Graphs with Absolute Value Functions

This paragraph introduces the concept of finding definite integrals from graphs, particularly when dealing with absolute value functions. It emphasizes the importance of recognizing that the absolute value function, F of the absolute value of X, is an even function. This property has significant implications for graphing and calculating integrals, as it allows for simplification by discarding the negative X portion of the graph and reflecting the positive part over the y-axis. The paragraph also outlines three different scenarios in which the absolute value might appear in integrals: taking the absolute value of the integral result, integrating the absolute value of the function directly, and integrating the function of the absolute value of X. Each scenario is approached with examples to illustrate the process.

05:02
📈 Evaluating Definite Integrals with Absolute Values: Methods and Examples

The second paragraph delves into the evaluation of definite integrals involving absolute values. It discusses the process of calculating the integral by considering the graph's positive region only, due to the even function property of absolute value functions. The paragraph explains how to handle the absolute value during integration by reflecting parts of the graph over the x-axis to account for negative areas turning positive. Several examples are provided to demonstrate different methods of calculating these integrals, such as directly summing areas, using symmetry to find equivalent regions, and applying the even function property to simplify calculations. The paragraph also touches on the use of a calculator for more complex integrals and concludes with a summary of the three ways absolute values can appear in definite integrals, offering a comprehensive guide to this mathematical concept.

Mindmap
Keywords
💡Definite Integrals
Definite integrals are a fundamental concept in calculus that represent the signed area under a curve between two points on the x-axis. In the context of the video, they are used to calculate the area under the graph of a function, which can be challenging when the function involves absolute values. The video discusses how to handle definite integrals with absolute values by considering the function's behavior and the effects of reflecting parts of the graph over the x-axis.
💡Absolute Value
The absolute value of a number is its distance from zero on the number line, regardless of direction. It is often denoted by vertical bars (e.g., |x|). In the video, the absolute value is used to transform the graph of a function, reflecting parts of the graph that are below the x-axis to above it. This transformation is crucial for calculating definite integrals because it changes the areas that are considered when integrating over certain intervals.
💡Even Function
An even function is a type of function that satisfies the condition f(x) = f(-x) for all x in its domain. This means that the function's graph is symmetric with respect to the y-axis. In the video, it is mentioned that the function f(x) = |x| is an even function because the graph of |x| is symmetric and only considers the positive part of the graph when reflected over the y-axis.
💡Graph Reflection
Graph reflection is a technique used in mathematics to create a mirrored image of a graph across an axis. In the video, the concept of reflecting the graph of a function over the y-axis is used to simplify the calculation of definite integrals involving absolute values. By reflecting the graph, negative areas under the curve become positive, which is essential for calculating the absolute value of the definite integral.
💡Signed Area
Signed area refers to the area under a curve that takes into account the sign (positive or negative) of the function values. Positive areas are above the x-axis, and negative areas are below the x-axis. The video explains that when dealing with absolute values, all signed areas become positive because the absolute value reflects negative areas above the x-axis.
💡Trapezoid and Triangle
In the context of the video, trapezoids and triangles are geometric shapes used to approximate the area under a curve when calculating a definite integral. The video provides examples where the area under the curve is broken down into trapezoids and triangles to facilitate the calculation of the integral, especially when the function involves absolute values.
💡Symmetry
Symmetry in mathematics refers to a property of an object or function where it can be transformed in some way, such as reflection, and still retain its overall structure. The video emphasizes the symmetry of even functions, particularly the absolute value function, which allows for simplification when calculating definite integrals by considering only one side of the graph and reflecting it as needed.
💡Y-Intercept
The y-intercept is the point where a line or curve crosses the y-axis in a Cartesian coordinate system. It is a key point in the video when creating the graph of the absolute value function. The y-intercept is used to determine the starting point of the graph and is important for calculating the area under the curve within specific intervals.
💡Integral Bounds
Integral bounds refer to the limits of integration, which define the interval over which the definite integral is calculated. The video discusses how to handle different types of integral bounds, especially when they are symmetric about the y-axis, which simplifies the calculation process due to the even nature of the absolute value function.
💡Calculus
Calculus is a branch of mathematics that deals with rates of change and accumulation of quantities. It is the broader subject within which the concepts of definite integrals and absolute values are studied. The video is focused on applying calculus techniques to find areas under curves represented by functions involving absolute values.
💡Numerical Evaluation
Numerical evaluation is the process of approximating the value of a mathematical expression, such as a definite integral, using numerical methods. In the video, the presenter mentions using a calculator for evaluating a particularly complex integral, demonstrating that numerical evaluation is a practical tool when analytical methods become too cumbersome.
Highlights

Discussing the process of finding definite integrals from graphs, emphasizing the complexity due to the involvement of absolute value functions.

Introduction of a key property: the absolute value of X (F of X) is an even function, which simplifies graph representation and integral calculations.

Explanation of discarding the graph for X less than zero and reflecting the remaining graph over the y-axis to achieve symmetry.

Demonstration of calculating definite integrals based only on the right-hand side of the graph due to the even function property.

Description of three scenarios where absolute value can appear in definite integrals, each requiring a different approach to calculation.

Method of taking the absolute value of a definite integral result, converting any negative result to a positive.

Technique for calculating the integral of the absolute value of a function by considering all signed areas and converting negative areas to positive.

Approach for dealing with the integral of the absolute value of a function from points A to B, using the property of even functions for simplification.

Example calculation of the absolute value of an integral from 4 to 9, resulting in a straightforward conversion to a positive value.

Illustration of reflecting parts of a graph to calculate the integral from negative 6 to negative 3 of the absolute value of a function.

Strategy for calculating the integral from negative 1 to 9 by identifying regions above the x-axis and summing their areas.

Common method of evaluating integrals by adding the absolute value of negative areas to positive areas for a simplified calculation.

Procedure for calculating the integral from negative nine to negative five by creating a graph of the absolute value function and using symmetry.

Explanation of using the right-hand side of the graph to evaluate integrals due to the even function property, demonstrated with an example from negative nine to negative five.

Example calculation of the integral from negative seven to negative three by recognizing symmetry and equating it to an integral from three to seven.

Use of the even function property to simplify the calculation of the integral from negative 3 to 3 by doubling the integral from 0 to 3 of the non-absolute value function.

Acknowledgment of the complexity of some integral calculations, where a calculator may be used for efficiency, as demonstrated with the integral from negative 3 to 3.

Summary of the three common ways absolute values appear in definite integrals and encouragement for further practice and understanding.

Transcripts

Browse More Related Video

AP Calculus Exam Tip: Definite Integral of Absolute Value Function

AP Calculus Exam Tip: Absolute Value of x over x, abs(x)/x

Definite integral of absolute value function | AP Calculus AB | Khan Academy

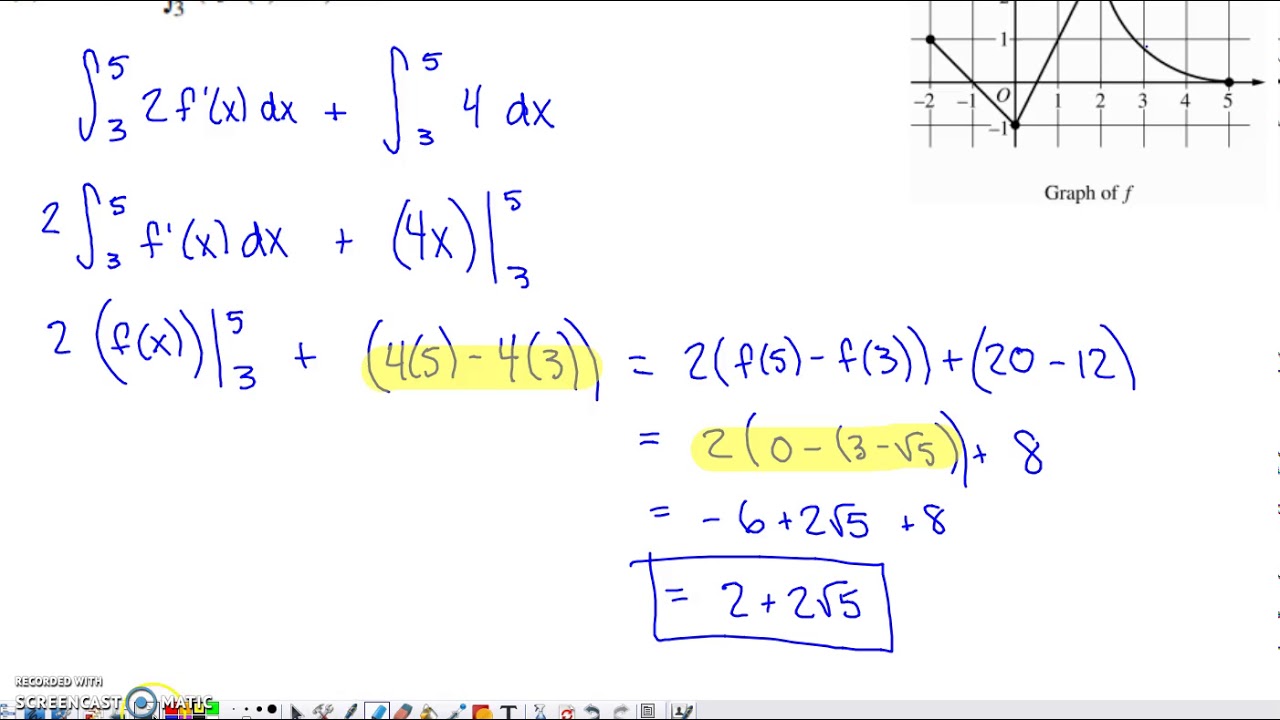
2019 AP Calculus AB & BC Free Response Question #3

Absolute Values: Defining, Calculating, and Graphing

4.4 - Properties of Definite Integrals

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Definite IntegralsAbsolute ValueGraph AnalysisMathematicsEven FunctionsCalculusIntegral EvaluationGraph TransformationSigned AreasReflected GraphsMath Tutorial