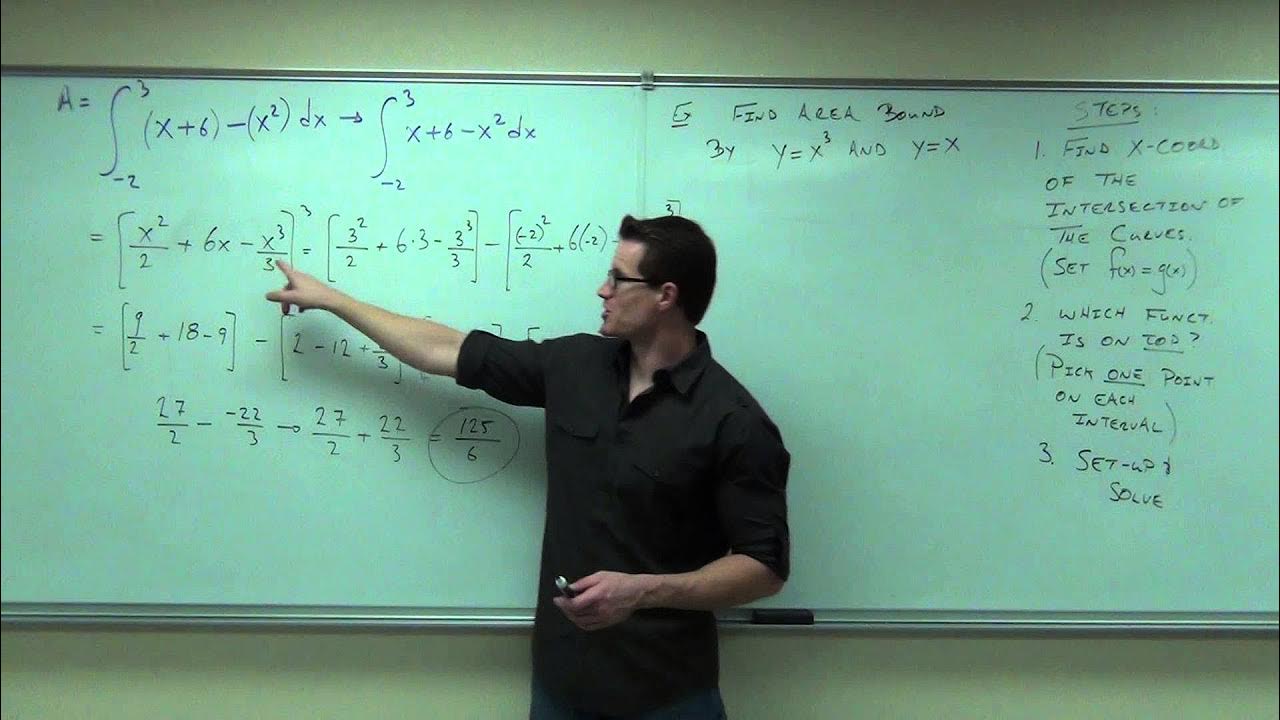Math 1325 Lecture 13 3
TLDRThis lecture, part of a calculus course for business and social sciences, delves into calculating the area between two curves. The process involves integrating the difference between the upper and lower functions over a shared domain. The lecturer illustrates this concept with diagrams and examples, emphasizing the importance of identifying which function is uppermost to determine the correct order of integration. The lecture also addresses common pitfalls and the need for multiple integrals when curves intersect. Practical applications, such as finding the average value of a function, are discussed, with a problem-solving approach that guides students through the steps of evaluating integrals and understanding the implications of the results. The average value is shown to be useful in real-world scenarios, such as calculating the average cost per unit for a range of products. The lecture concludes with a reminder of the foundational concepts and the importance of practice in mastering integral calculus.
Takeaways
- 📐 The area between two curves can be found by integrating the upper function and subtracting the integral of the lower function over a common interval.
- 📈 To find the area under a curve, one can use rectangles to estimate or directly calculate the integral of the function over the desired domain.
- 🔍 When curves intersect, it's important to graph the functions over the interval to determine which is the upper function and to find the points of intersection.
- 📉 For regions bounded by two curves, the area is calculated as the integral of the upper curve minus the lower curve from the lower boundary to the upper boundary.
- ⚖️ The average value of a function over an interval can be used to find the area under the curve above the x-axis, which is the integral of the function divided by the width of the interval.
- 🧮 The average value of a function is calculated by dividing the integral of the function over an interval by the width of that interval (B - A).
- 💡 In problems where functions cross over, it's necessary to perform multiple integrals, each corresponding to a different section where one function is above the other.
- 📊 To find the area enclosed by two curves that are totally bounded, locate the points of intersection which define the boundaries of the region.
- 📘 When solving for the area between curves, it's essential to evaluate the integrals at the correct upper and lower limits and then subtract the results to find the area.
- 💭 The concept of average value is not only useful for finding areas but also for determining average costs in business and social science applications.
- 📌 The average cost per unit is found by dividing the total cost function by the number of units (X), which is different from the average total cost for a range of units.
Q & A
What is the main topic of lecture thirteen, point three?
-The main topic of the lecture is the area between two curves in calculus for business and social sciences.
How is the area under a curve estimated?
-The area under a curve is estimated by creating a series of rectangles and using the integral over the curve.
What is the formula for finding the area between two curves?
-The formula for the area between two curves is the integral from A to B of the upper function f(x) minus the lower function g(x), or ∫ from A to B [f(x) - g(x)] dx.
What is the condition for f(x) to be considered the upper function?
-f(x) is considered the upper function if it is either equal to or greater than g(x) on the entire interval under consideration.
How do you determine which function is the upper function?
-You can determine the upper function by graphing both functions over the interval and observing which one is on top or by calculating the value of both functions at a point within the interval.
What is the process for finding the area enclosed by two curves that intersect?
-To find the area enclosed by two intersecting curves, you first find the points of intersection, then calculate the integral for each region bounded by the curves and the x-axis, and sum these areas.
How do you find the points of intersection for two functions?
-You can find the points of intersection by setting the two functions equal to each other and solving for x, which gives you the x-coordinates of the intersection points.
What is the average value of a function over an interval?
-The average value of a function over an interval is found by dividing the definite integral of the function over the interval by the width of the interval (B - A).
How is the average cost per unit calculated?
-The average cost per unit is calculated by dividing the total cost function by the number of units (X).
What is the significance of the average value in the context of the cost function?
-The average value of the cost function over an interval represents the average total cost for producing a number of units within that interval.
Why is it important to calculate the average value of a function?
-Calculating the average value of a function is important as it provides insight into the average behavior of the function over an interval, which can be useful in various applications, such as determining average costs in business.
Outlines
📚 Introduction to Calculating Areas Between Curves
The video begins with an introduction to Lecture 13.3, focusing on the area between two curves in the context of Math 1325 Calculus for Business and Social Sciences. The lecturer recaps the method of finding the area under a curve using rectangles and integrals. The key concept introduced is that the area between two curves can be found by taking the integral of the upper function and subtracting the integral of the lower function over a common domain. The lecturer emphasizes the importance of identifying which function is the upper one and suggests graphing both functions over the interval to ensure there are no intersections or crossovers. A step-by-step approach to solving such problems is provided, with an example problem calculating the area bounded by y=x^2+4, y=x, and the lines x=0 and x=3.
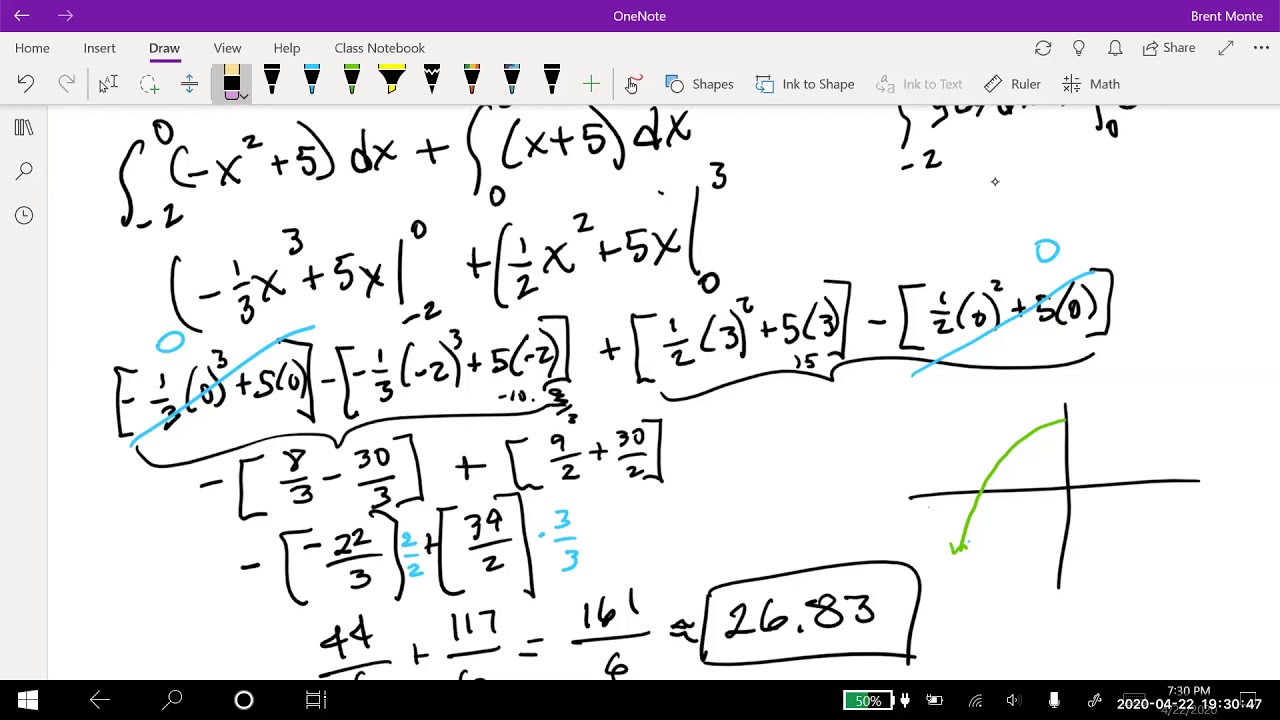
🔍 Dealing with Enclosed Areas and Intersections
The second paragraph delves into finding the area enclosed by two curves that are completely bounded by them. The lecturer explains that when functions cross over, it's essential to find the points of intersection as these define the boundaries of the enclosed region. A problem involving finding the area enclosed by y=x^2 and y=2x+3 is presented. The process involves setting the two equations equal to each other to find the intersection points, which serve as the limits for the integral. The integral is then evaluated for each section, taking the upper function minus the lower function, and the results are summed to find the total enclosed area. The paragraph also touches on the concept of average value, relating it to the area under a curve and the average height of the function over an interval.
💡 Average Value and Cost Application
The final paragraph discusses the concept of average value in a practical context, using the cost function C(x) = 400 + x + 0.3x^2 to find the average cost per unit for producing between 10 to 20 lamps. The lecturer demonstrates how to calculate the average value of a function over an interval, which in this case represents the average total cost for producing a certain number of lamps. The distinction between the average total cost and the average cost per unit is clarified, with the latter being found by dividing the total cost function by the number of units (x). An example calculation is shown, resulting in an average cost of $23 per lamp for 40 units. The paragraph concludes with a reminder of the importance of understanding the average value as it applies to the function in question, whether it represents cost, revenue, or another variable.
Mindmap
Keywords
💡Area between two curves
💡Integral
💡Rectangles
💡Domain
💡Upper and lower functions
💡Points of intersection
💡Average value
💡Cost function
💡Total cost
💡Average cost per unit
💡Graphical representation
Highlights
Calculating the area between two curves can be done by subtracting the integral of the lower curve from the integral of the upper curve over a common domain.
The function that is above or greater than the other over the interval is considered the upper function.
When curves switch sides, it may be necessary to perform multiple integrals to find the area between them.
To find the area bounded by curves, identify the upper and lower functions and their respective domains.
Graphing functions over the interval can help visualize intersections and determine which function is upper or lower.
The integral of the difference between the upper and lower functions over the domain gives the area between the curves.
For areas enclosed by curves, find the points of intersection to determine the boundaries for the integral.
Setting two functions equal to each other can help find the points of intersection for curves.
The average value of a function over an interval can be found using the integral and the width of the interval.
The area under a curve can also be calculated by multiplying the average value of the function by the width of the interval.
The average total cost for producing a range of units can be found using the average value of the cost function.
The average cost per unit is found by dividing the total cost function by the number of units (X).
For problems with multiple areas due to crossovers, calculate each area separately using its own integral.
When evaluating definite integrals, plug in the upper and lower limits and subtract to find the area.
Practicing integral calculations is essential for solving problems involving areas between curves.
The average value of a function represents the average height over an interval and can be used to find the area under a curve.
In practical applications, such as calculating average costs, integrals and average values provide a way to estimate totals over a range of values.
For problems involving a change in which function is upper or lower, adjust the order of integration to reflect the current interval.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: