Entropy of Free Expansion
TLDRThe video script delves into the concept of entropy in physics, presenting it through three distinct yet interconnected perspectives. Firstly, entropy is defined as a measure of the number of microstates associated with a given macro state, quantified by Boltzmann's constant times the natural logarithm of the number of microstates. Secondly, it is portrayed as a measure of disorder, where an increase in entropy corresponds to a more disordered state, exemplified by the free expansion of an ideal gas into a larger volume. Thirdly, entropy is viewed as a measure of information, where higher entropy indicates a greater lack of information about the system's microstate. The script illustrates these ideas through an example involving the expansion of gas, showing how entropy increases as particles spread out, reflecting the second law of thermodynamics that the entropy of the universe tends to increase. This comprehensive exploration of entropy provides a clear understanding of its multifaceted nature in physics.
Takeaways
- 🔢 Entropy is a measure of the number of microstates associated with a given macro state, often denoted by the letter 'S' and defined by Boltzmann's constant times the natural log of the number of microstates (Ω).
- 📈 Entropy can be thought of as a measure of disorder, where an increase in entropy corresponds to an increase in the system's disorder.
- 📚 Entropy is also a measure of the lack of information about a system, directly related to the number of microstates associated with a macro state.
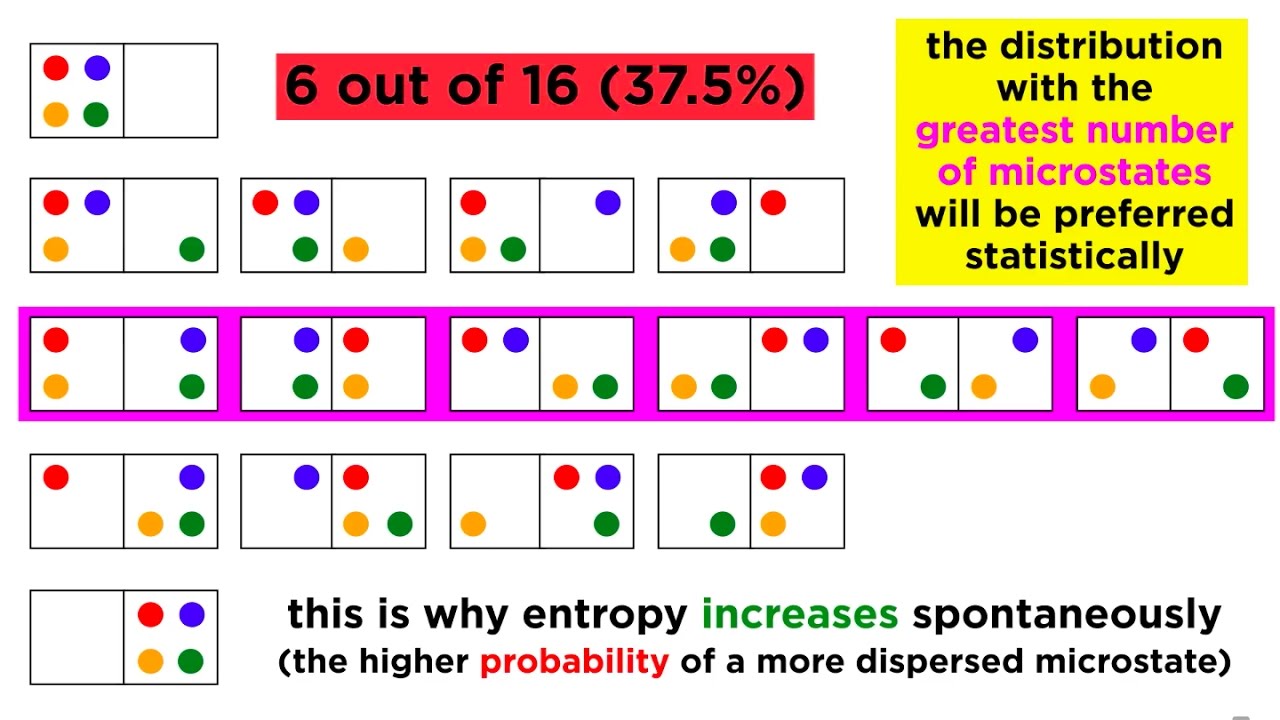
- 📊 In the example of free expansion, when a partition is removed, allowing gas particles to spread out, the entropy of the system increases as there are more microstates available to the particles.
- 🔄 The change in entropy (ΔS) is calculated as the final entropy minus the initial entropy, which in the free expansion example is Boltzmann's constant times the natural log of the ratio of final to initial microstates.
- ↗️ The second law of thermodynamics states that the entropy of the universe is always increasing, which is illustrated by the increase in entropy when particles are allowed to spread out.
- 🚫 While it's theoretically possible to decrease the entropy of a system by forcing particles back into a more ordered state, doing so would require work and create other forms of entropy, ensuring the total entropy of the universe still increases.
- 🧹 Entropy's increase signifies a loss of information about the specific microstate each particle occupies, as the system moves from a more ordered to a more disordered state.
- 🔄 The concept of entropy is central to understanding the direction of spontaneous processes in thermodynamics, as it reflects the system's tendency to move toward a state of higher probability.
- 🌌 Entropy's role in the universe's evolution is profound, as it underlies the progression from ordered to disordered states, which is a fundamental aspect of the second law of thermodynamics.
- ⚙️ Understanding entropy's relationship with microstates and macrostates is crucial for comprehending the statistical nature of thermodynamics and the behavior of particles in a system.
Q & A
What is entropy in the context of physics?
-Entropy in physics is a measure of the number of microstates associated with a given macro state, often denoted by the letter 's'. It is also a measure of disorder and a lack of information about the system's specific state.
How is entropy related to the number of microstates?
-Entropy is directly proportional to the number of microstates (denoted as Omega) associated with a macro state. It is given by Boltzmann's constant times the natural logarithm of the number of microstates.
What does an increase in entropy signify in terms of microstates?
-An increase in entropy signifies that there are more possible microstates associated with the macro state, indicating a higher degree of uncertainty or a larger number of potential configurations the system can have.
How does the concept of entropy relate to the idea of disorder?
-Entropy is considered a measure of disorder. A system with higher entropy is more disordered, as it has more possible arrangements of its components, whereas a system with lower entropy is more ordered with fewer arrangements.
What is the significance of entropy in terms of information?
-Entropy signifies the lack of information about the specific microstate of a system when only the macro state is known. The more microstates associated with a macro state, the less information we have about the system's precise configuration.
What happens to the entropy of a system when an ideal gas expands freely into a larger volume?
-The entropy of the system increases. This is because when the gas expands freely, the particles spread out and can occupy more locations, leading to a higher number of microstates and thus a higher entropy.
How does the second law of thermodynamics relate to entropy?
-The second law of thermodynamics states that the entropy of the universe is always increasing. This means that natural processes tend to move towards a state of higher entropy, indicating a greater degree of disorder.
Can the entropy of a system decrease?
-While the entropy of an isolated system cannot decrease due to the second law of thermodynamics, it is theoretically possible for the entropy of a subsystem to decrease if work is done on it. However, when considering the entire system including the work done, the overall entropy still increases.
What is the mathematical expression for the change in entropy when particles are allowed to freely expand?
-The change in entropy (ΔS) is given by Boltzmann's constant (KB) times the natural logarithm of the ratio of the final to initial number of microstates (ln(2^N)), where N is the number of particles.
How does the concept of entropy apply to the example of a room's cleanliness?
-Entropy can be used as an analogy for the state of a room. A clean room, where items are in specific places, represents a state of lower entropy, while a messy room with items scattered represents a state of higher entropy, indicating more possible arrangements of the items.
What is Boltzmann's constant, and how does it relate to entropy?
-Boltzmann's constant (KB) is a physical constant that relates the temperature of a system to the energy of its particles. In the context of entropy, it is used as a multiplier to ensure the correct units for entropy, which is then expressed as KB times the natural logarithm of the number of microstates.
Why is it important to understand the concept of entropy in physics?
-Understanding entropy is crucial in physics because it is a fundamental concept that describes the thermodynamic properties of systems, predicts the direction of natural processes, and is central to the second law of thermodynamics, which governs the behavior of energy and disorder in the universe.
Outlines
🔍 Introduction to Entropy Concepts
The video introduces the concept of entropy in physics, highlighting that it has multiple definitions and ways of understanding. It discusses entropy in terms of microstates and macrostates, explaining how entropy (denoted by 's') is a function that tells us the number of microstates associated with a given macrostate. The entropy is calculated using Boltzmann's constant and the natural logarithm of the number of microstates (Ω). The video also touches on entropy as a measure of disorder and a measure of lack of information, correlating with the microstate-macrostate relationship. An example of free expansion of an ideal gas is used to illustrate these concepts.
📈 Calculating Entropy Change in Free Expansion
This paragraph delves into calculating the change in entropy when an ideal gas undergoes free expansion from one half of a box to filling the entire box after the partition is removed. It explains the process of determining the number of microstates in both the initial and final states, using 'X' to represent the number of states each particle can occupy. The entropy of the initial state is given by Boltzmann's constant times the natural log of the total microstates (X^N), and the final state has double the volume and thus 2X^N microstates. The change in entropy is computed as the final entropy minus the initial entropy, resulting in Boltzmann's constant times the natural log of 2 to the power of N, indicating an increase in entropy.
🌐 Interpreting Entropy Through its Definitions
The video concludes by interpreting the increase in entropy through the three definitions provided earlier. It relates the increase in possible microstates to the final state of the gas expansion, indicating a higher entropy due to more microstates being associated with the macro state. It also discusses entropy as a measure of disorder, with the final state of the gas being more disordered than the initial state. Furthermore, the video addresses entropy as a measure of lack of information, explaining that with the expansion, we lose specific information about the location of each particle, thus increasing our lack of information and the entropy of the system. Finally, it connects the observed increase in entropy to the second law of thermodynamics, which states that the entropy of the universe always increases, and notes that even if the particles were forced back into the original state, the total entropy of the universe would still increase when considering the entire process.
Mindmap
Keywords
💡Entropy
💡Microstates
💡Macrostates
💡Boltzmann's Constant
💡Free Expansion
💡Disorder
💡Lack of Information
💡Second Law of Thermodynamics
💡Natural Logarithm
💡Partition
💡Ideal Gas
Highlights
Entropy in physics has multiple definitions and ways of thinking about it.
One definition of entropy is the number of microstates associated with a given macro state.
Entropy is often denoted by the letter 's' and is given by Boltzmann's constant times the natural log of the number of microstates (Ω).
Entropy can be thought of as a measure of disorder within a system.
Entropy also represents a measure of lack of information, directly correlated with the microstate-macrostate relationship.
An example of entropy change is provided by considering the free expansion of an ideal gas.
The total number of microstates in a system is calculated by multiplying the possible states for each particle.
The initial and final entropy states of the gas are computed to determine the change in entropy during expansion.
The change in entropy is calculated using Boltzmann's constant and the natural log function.
An increase in entropy corresponds to an increase in the number of possible microstates associated with the macro state.
Entropy is interpreted as a measure of disorder, with higher entropy indicating a more disordered state.
The concept of entropy as a lack of information is illustrated by the inability to track individual particles after expansion.
The second law of thermodynamics is introduced, stating that the entropy of the universe always increases.
Attempting to decrease entropy by forcing particles back into a previous state would ultimately increase the total entropy of the universe.
The video concludes by emphasizing the multifaceted nature of entropy and its practical computation for specific states.
Transcripts
Browse More Related Video
The Second Law of Thermodynamics: Heat Flow, Entropy, and Microstates

Reconciling thermodynamic and state definitions of entropy | Physics | Khan Academy
24. The Second Law of Thermodynamics (cont.) and Entropy

The Biggest Ideas in the Universe | 20. Entropy and Information

More on entropy | Thermodynamics | Physics | Khan Academy

Brian Cox explains why time travels in one direction - BBC
5.0 / 5 (0 votes)
Thanks for rating: