The Second Law of Thermodynamics: Heat Flow, Entropy, and Microstates
TLDRThis video script delves into the second law of thermodynamics, introducing entropy as a key concept. It explains the historical development through Sadi Carnot's work on heat engines, illustrating how no engine can achieve 100% efficiency due to irreversible processes like friction. The script further explores entropy as a measure of a system's disorder, highlighting its inevitable increase in the universe for spontaneous processes. It concludes with Ludwig Boltzmann's microstates concept, providing a statistical explanation for the natural tendency towards greater disorder.
Takeaways
- 🔧 The second law of thermodynamics introduces the concept of entropy, which is central to understanding the limitations of heat engines.
- 🚂 Sadi Carnot's work on heat engines, which use heat to do work, led to the formulation of the second law of thermodynamics.
- ♨️ Heat engines transfer excess heat not used for work to a cold reservoir, illustrating the inherent inefficiency in these systems.
- 🔄 Carnot's principle states that a process is reversible if the system and surroundings can return to their original state, which is impossible in real engines due to friction and sound.
- 🚫 The second law asserts that no cyclic process can convert all heat into work, some heat will always be lost to the surroundings, contrasting the first law of thermodynamics.
- ↔️ Heat spontaneously flows from high to low temperature regions, reinforcing the idea of heat loss in heat engines.
- 🌐 The second law implies that the entropy of the universe increases for any spontaneous process, never decreases, indicating a trend towards disorder.
- 📈 Entropy is a state function measured in joules per Kelvin and represents the loss of a heat engine's ability to do work.
- 🔄 For a reversible process, the change in entropy is zero, but since no process is truly reversible, the universe's entropy always increases.
- 🧩 Entropy increase is associated with the concept of microstates, where systems tend towards configurations with the most microstates, leading to greater disorder.
- 🌌 The philosophical implications of entropy suggest that the universe moves towards maximum disorder, with local order formation being offset by increased universal disorder.
Q & A
What is the second law of thermodynamics?
-The second law of thermodynamics introduces the concept of entropy and states that no cyclic process can convert some quantity of heat entirely into work, and some of this heat will always be lost to the surroundings.
Who is Sadi Carnot and what is his contribution to the second law of thermodynamics?
-Sadi Carnot was a French scientist who studied heat engines. His work led to the understanding that the maximum work done by a heat engine in one cycle is equal to the heat input minus the heat output, which is the basis for the second law of thermodynamics.
What is a heat engine and how does it relate to the second law?
-A heat engine is a device that absorbs heat and uses it to do work, like the steam locomotives of the 19th century. The second law of thermodynamics is derived from the study of heat engines, explaining the limitations of converting heat into work due to inefficiencies and entropy.
What is the concept of Carnot's principle?
-Carnot's principle states that the only way to achieve 100% efficiency in a heat engine would be if every process in the engine were completely reversible, allowing the system and surroundings to return to their original state. However, this is not physically possible due to factors like friction and sound.
Why can't a heat engine operate at 100% efficiency?
-A heat engine cannot operate at 100% efficiency because of the inherent inefficiencies in real engines, such as friction and sound, which cause some energy to be lost to the surroundings. Even a hypothetical perfect heat engine, known as a Carnot engine, cannot achieve 100% efficiency due to the mathematical limitation of heat flow.
What is entropy and how is it related to the second law of thermodynamics?
-Entropy is a state function that represents the inevitable partial loss of a heat engine's ability to do work. It is measured in joules per Kelvin and is related to the second law of thermodynamics as it quantifies the amount of energy that cannot be converted into work, indicating the direction of spontaneous heat flow.
How is the change in entropy for a reversible process calculated?
-The change in entropy for a reversible process is calculated as the heat divided by the Kelvin temperature of the system. For a Carnot engine, this change in entropy is zero, indicating perfect reversibility.
What does it mean for the entropy of the universe to increase?
-The increase in the entropy of the universe for any spontaneous process means that the overall disorder of the universe is always increasing. This is another way of stating the second law of thermodynamics, suggesting that the universe tends towards a state of maximum disorder.
What is the philosophical implication of the second law of thermodynamics?
-The philosophical implication of the second law is that it suggests the universe tends toward a state of maximum disorder. While order can spontaneously form locally, such as in the formation of ice or living organisms, it is always accompanied by an increase in the universe's overall disorder.
How does Ludwig Boltzmann's concept of microstates help explain entropy?
-Ludwig Boltzmann's concept of microstates provides a statistical understanding of entropy. A microstate is a specific configuration of particles and energies in a system. Entropy increases as the system tends towards more disorder because the most probable distribution of particles and energy is the one with the most microstates, indicating a higher probability of increased disorder.
Can you provide an example to illustrate the concept of microstates and entropy?
-An example of microstates and entropy is distributing four balls of different colors into two boxes. The most probable distribution, which has the highest number of microstates, is when there are two balls in each box. This distribution has six possible arrangements out of a total of 16, illustrating why entropy tends to increase as systems tend toward more disordered configurations.
Outlines
🔧 The Second Law of Thermodynamics and Entropy
This paragraph delves into the intricacies of the second law of thermodynamics, which introduces the concept of entropy as a measure of a system's irreversibility. It discusses the historical context of Sadi Carnot's work on heat engines and how they absorb heat to perform work, with the inevitable transfer of excess heat to a colder reservoir. The concept of Carnot's principle is introduced, which states that no engine can be 100% efficient due to the irreversibility of real-world processes, such as friction and sound production. The second law is then articulated in two ways: as a limitation on converting heat entirely into work and as the spontaneous flow of heat from hot to cold. The paragraph concludes with an introduction to entropy as a state function, its calculation for reversible processes, and the philosophical implications of the universe's tendency towards increasing disorder.
📚 Entropy, Microstates, and the Statistical Nature of Systems
The second paragraph explores the statistical mechanics perspective on entropy, explaining it as a measure of the number of possible microstates in a system. It introduces Ludwig Boltzmann's equation for entropy, which relates it to the Boltzmann constant and the logarithm of the number of microstates. The paragraph uses the example of distributing balls between boxes to illustrate how systems tend towards the most probable distribution with the highest number of microstates, thereby increasing entropy. It concludes by emphasizing the difficulty of understanding entropy and encourages viewers to focus on the basics of the second law's derivation, while also inviting them to subscribe for more content and support the creator on Patreon.
Mindmap
Keywords
💡Second Law of Thermodynamics
💡Entropy
💡Heat Engine
💡Carnot's Principle
💡Efficiency
💡Reversible Process
💡Microstates
💡Boltzmann's Equation
💡Spontaneous Process
💡Disorder
Highlights
The second law of thermodynamics introduces the concept of entropy, a central and often confusing concept in physics.
Sadi Carnot's work on heat engines led to the formulation of the second law, highlighting the relationship between heat input, work done, and heat output.
Heat engines, such as 19th-century steam locomotives, use heat to do work but also transfer excess heat to a cold reservoir.
Carnot's principle states that no engine can be 100% efficient due to irreversibilities like friction and sound.
The second law asserts that no cyclic process can convert all heat into work without some heat being lost to the surroundings.
Heat spontaneously flows from high to low temperature, illustrating the directionality of energy transfer.
The second law implies that even a hypothetical perfect Carnot engine cannot achieve 100% efficiency due to mathematical limitations of heat flow.
Entropy is a state function that measures the loss of a heat engine's ability to do work, represented in joules per Kelvin.
The change in entropy for a reversible process is given by the formula heat divided by temperature.
For a Carnot engine, the change in entropy is zero, suggesting a reversible process with no energy loss.
The entropy of the universe increases for any spontaneous process, indicating a natural tendency towards disorder.
The philosophical implications of entropy suggest that the universe moves towards maximum disorder over time.
Local order, such as in the formation of ice or living organisms, is accompanied by an increase in the universe's overall disorder.
Ludwig Boltzmann's concept of microstates helps rationalize entropy, showing that systems tend towards configurations with more microstates.
The most probable distribution of particles in a system is the one with the highest number of microstates, as illustrated by the example of distributing balls among boxes.
Entropy increase is a fundamental aspect of closed systems, whether it involves the dispersal of matter or heat energy.
Understanding the second law of thermodynamics and its derivation is crucial for grasping basic principles in physics.
Transcripts
Browse More Related Video

The Most Misunderstood Concept in Physics
24. The Second Law of Thermodynamics (cont.) and Entropy

Entropy of Free Expansion
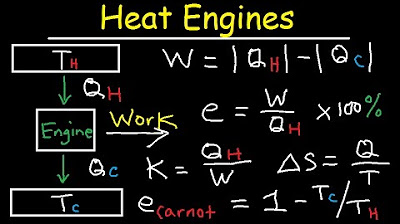
Carnot Heat Engines, Efficiency, Refrigerators, Pumps, Entropy, Thermodynamics - Second Law, Physics
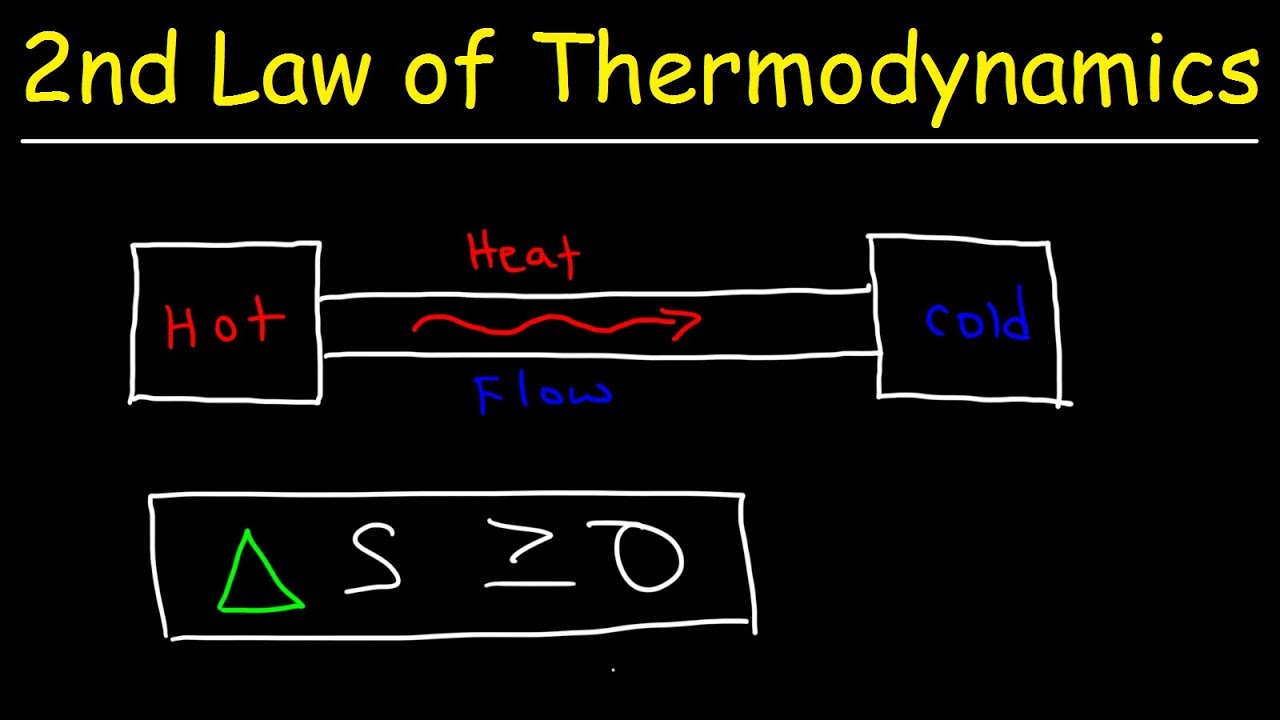
Second Law of Thermodynamics - Heat Energy, Entropy & Spontaneous Processes

Carnot Engine
5.0 / 5 (0 votes)
Thanks for rating: