24. The Second Law of Thermodynamics (cont.) and Entropy

YaleCourses

22 Sept 200871:47

EducationalLearning

32 Likes 10 Comments

TLDRThe video script delves into the concept of the Carnot engine, a theoretical construct that sets the upper limit for the efficiency of any heat engine. It explains the Carnot cycle, which involves isothermal expansion and compression, adiabatic expansion, and further isothermal compression, highlighting the importance of the engine's reversible nature. The script further explores the Second Law of Thermodynamics, which stipulates that the entropy of the universe can only increase or remain the same, never decrease. This law is demonstrated through various examples, such as heat transfer between bodies at different temperatures and the mixing of hot and cold water. The script also introduces Boltzmann's formula for entropy, which provides a statistical interpretation of entropy in terms of the number of microstates that correspond to a given macrostate. The lecturer emphasizes that entropy is a measure of disorder and that the Second Law is fundamentally a statistical law, explaining why certain spontaneous processes occur and others do not. The summary underscores the significance of entropy in understanding the directionality of time and the behavior of systems in the universe.

Takeaways

🔥 The Carnot engine is a theoretical construct that operates at the highest possible efficiency between two temperatures.
🔧 Efficiency of the Carnot engine is given by 1 - T2/T1, where T1 and T2 are the absolute temperatures of the hot and cold reservoirs.
🚫 No real engine can surpass the efficiency of a Carnot engine, which is a consequence of the Second Law of Thermodynamics.
🔄 The Carnot cycle consists of two isothermal and two adiabatic processes, and it is a reversible cycle, allowing the engine to operate continuously.
📐 The concept of entropy is central to understanding the Second Law of Thermodynamics, which states that the total entropy of a closed system can never decrease over time.
↔️ Entropy is a measure of the number of microscopic configurations that correspond to a given macroscopic state, with higher entropy indicating more configurations.
⏲️ The Second Law of Thermodynamics dictates that natural processes occur in the direction of increasing entropy, often described as the 'arrow of time'.
🔩 The change in entropy for a reversible process is calculated by integrating dQ/T over the cycle, where dQ is the infinitesimal heat transfer and T is the temperature.
💡 Ludwig Boltzmann provided the statistical interpretation of entropy, with his famous formula S = k log Ω, where Ω is the number of microstates and k is the Boltzmann constant.
⛄️ When two bodies of different temperatures are put in contact, heat flows from the hotter to the colder body until thermal equilibrium is reached, resulting in an increase in total entropy.
🚿 In an isolated system, such as a gas expanding freely into a vacuum, the entropy increases even though the temperature remains constant, reflecting the increased number of possible microstates.

Q & A

What is the Carnot engine and how does it work?
-The Carnot engine is a theoretical heat engine that operates on the reversible Carnot cycle. It consists of a gas that undergoes a cycle with four stages: isothermal expansion, adiabatic expansion, isothermal compression, and adiabatic compression. The engine exchanges heat with two temperature reservoirs, taking in heat at a higher temperature and expelling some of it at a lower temperature, with the difference being converted into work.
What is the efficiency of a Carnot engine?
-The efficiency of a Carnot engine is given by 1 - (T2/T1), where T1 is the temperature of the hot reservoir and T2 is the temperature of the cold reservoir. This formula represents the maximum possible efficiency for a heat engine operating between two temperatures.
Why can't any engine be more efficient than the Carnot engine?
-Carnot's theorem states that no engine can be more efficient than a Carnot engine operating between the same two temperatures. This is because the Carnot engine is a reversible engine, and it's based on the second law of thermodynamics, which postulates that it's impossible to transfer heat from a colder to a hotter body without additional effects, such as work being done.
What is the concept of entropy and how is it related to the second law of thermodynamics?
-Entropy is a thermodynamic property that measures the number of specific ways in which a system may be arranged, commonly understood as a measure of disorder. The second law of thermodynamics states that the total entropy of an isolated system can never decrease over time, and is constant if and only if all processes are reversible. For irreversible processes, the entropy of the universe increases.
How does the concept of entropy explain spontaneous processes?
-Entropy provides a statistical explanation for the direction of spontaneous processes. A process is spontaneous if it leads to an increase in the total entropy of the universe. If a process would lead to a decrease in total entropy, it cannot occur spontaneously.
What is the microscopic interpretation of entropy?
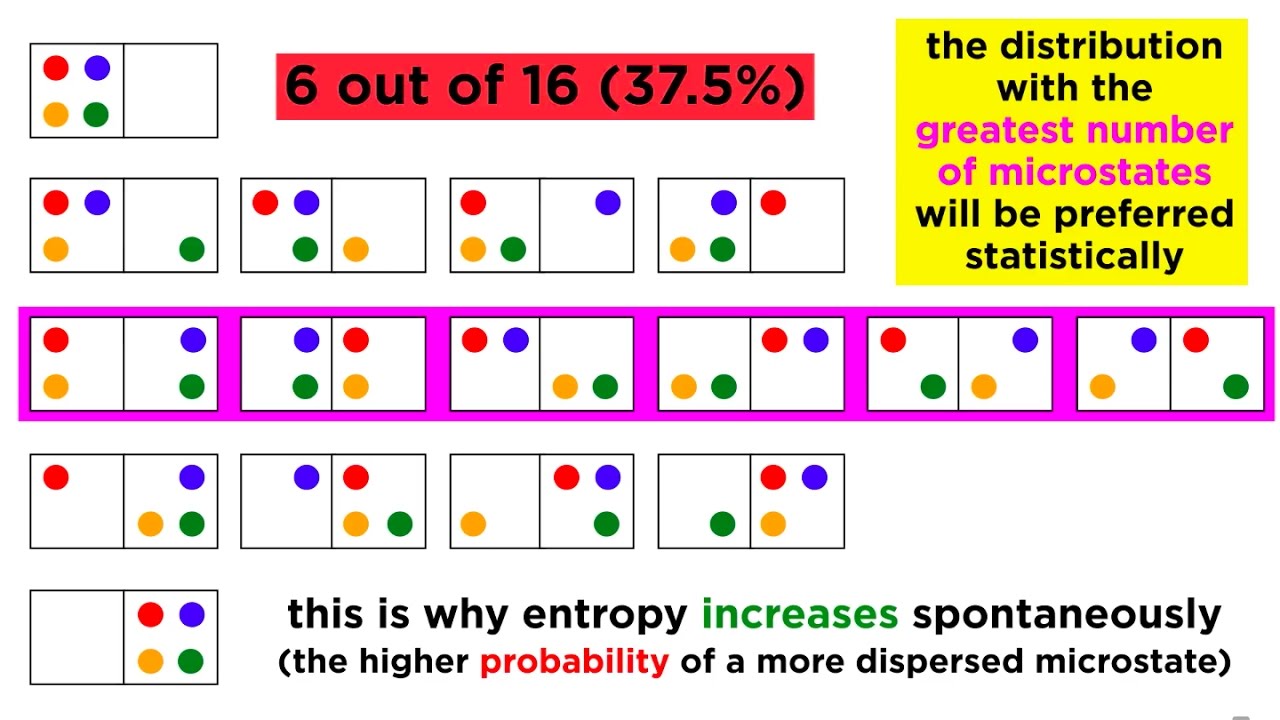
-The microscopic interpretation of entropy comes from statistical mechanics. It is given by Boltzmann's formula S = k log Ω, where S is the entropy, k is the Boltzmann constant, and Ω is the number of microstates that correspond to a given macrostate. It essentially counts the number of ways the system can be arranged, with higher entropy corresponding to a greater number of possible arrangements.
How does the Carnot engine relate to the concept of reversible and irreversible processes?
-The Carnot engine is an example of a reversible engine, meaning that every step in its cycle can be run in reverse without any net change in the system or surroundings. This reversibility is key to its high efficiency. In contrast, real-world engines involve irreversible processes, such as friction, which increase the entropy of the universe and thus reduce efficiency.
What is the practical significance of the Carnot engine in modern engineering?
-While the Carnot engine is a theoretical construct and cannot be built in practice, it provides an upper limit on the efficiency that any real engine can achieve. This helps engineers understand the theoretical maximum performance of heat engines and guides the design of more efficient real-world engines.
How does the Carnot cycle demonstrate the conservation of energy?
-The Carnot cycle demonstrates the conservation of energy through the relationship between heat (Q) and work (W). In a cyclic process like the Carnot cycle, the net work done by the system is equal to the difference in heat exchanged with the reservoirs (W = Q1 - Q2), where Q1 is the heat absorbed and Q2 is the heat rejected, showing that energy is conserved.
What is the role of temperature in the calculation of entropy change during a reversible isothermal process?
-During a reversible isothermal process, the change in entropy is calculated by dividing the heat transferred by the temperature at which the process occurs (∆S = ∫dQ/T). This division by temperature accounts for the temperature dependence of the heat capacity and ensures that the entropy change is a state function, independent of the path taken.
How does the expansion of a gas into a vacuum illustrate the concept of entropy increase?
-The expansion of a gas into a vacuum is an example of a spontaneous process that leads to an increase in entropy. When the partition is removed, the gas molecules spread out to occupy the entire available volume, leading to a greater number of possible microscopic arrangements (higher disorder). This increase in the number of microstates corresponds to an increase in entropy, in accordance with the second law of thermodynamics.

Outlines

00:00

🔥 Carnot Engine Cycle Explained

The paragraph describes the workings of a Carnot engine, a theoretical engine that operates on a reversible cycle between two temperature reservoirs. It explains the isothermal expansion and compression stages, the adiabatic expansion and compression stages, and how heat Q_1 enters the system and Q_2 is rejected, resulting in work done by the engine. The schematic of the Carnot engine is also mentioned, emphasizing its cyclic nature and the conservation of energy principle.

05:01

📐 Calculating Carnot Engine Efficiency

This section focuses on how to calculate the efficiency of a Carnot engine using the temperatures of the heat source (T_1) and the exhaust (T_2). It details the mathematical derivation involving the integration of work done and the concept of adiabatic curves. The final result for the efficiency of the Carnot engine is given as 1 - T_2/T_1, which is a crucial takeaway for the discussion.

10:03

🔧 Carnot's Claim and Reversible Engines

The paragraph discusses Carnot's claim that no engine can surpass the efficiency of a Carnot engine. It introduces the concept of a reversible engine, which can run in either direction without losing energy. The idea of a Carnot refrigerator is also brought up, showing that the Carnot engine and refrigerator are essentially the same machine operating in different ways. The paragraph concludes with a demonstration of why no engine can beat the Carnot engine based on the Second Law of Thermodynamics.

15:04

🔄 Entropy and the Carnot Cycle

The concept of entropy is introduced as a state variable that remains constant for a closed system returning to its initial conditions. The paragraph explains the relationship between heat transfer in a Carnot cycle and the calculation of entropy change. It also touches on the theoretical implications of entropy in determining the efficiency of heat engines and the direction of spontaneous processes.

20:07

🔍 Understanding Entropy Changes

This section delves into calculating entropy changes for specific processes, such as heating a substance or the isothermal expansion of an ideal gas. It emphasizes the importance of the system being near equilibrium during these processes. The entropy formula mC log(T_final/T_initial) is derived for heating or cooling a substance, and nR log(V_final/V_initial) for the isothermal expansion of a gas.

25:11

🔗 Entropy as a State Variable

The paragraph establishes entropy as a state variable like internal energy, with a fixed value at any given point in a system. It discusses the properties of entropy in the context of the Carnot cycle and how it behaves during reversible and irreversible processes. The concept that the entropy change in a closed system must be zero if the process is cyclical is highlighted.

30:11

🚫 Forbidden Processes and Entropy

This section uses the concept of entropy to explain why certain natural processes are forbidden from occurring spontaneously. It covers examples such as a bottle shattering or an egg breaking not reverting to its original state, illustrating that these processes would result in a decrease in entropy, which is not allowed by the Second Law of Thermodynamics.

35:13

🌡️ Entropy and Spontaneous Mixing

The paragraph explores the entropy changes when hot and cold bodies are mixed, leading to a uniform temperature. It shows mathematically that the entropy of the universe increases when two bodies at different temperatures are combined, resulting in a higher entropy state. This increase in entropy is why such mixing occurs spontaneously, as it is a natural progression towards a state of higher entropy.

40:18

📉 Entropy and Equilibrium States

The focus is on the calculation of entropy change for a gas expanding freely into a vacuum, transitioning from one equilibrium state to another. The paragraph clarifies that the entropy change should be computed for a process that keeps the system near equilibrium, even if the actual process was not in equilibrium. It also explains that the entropy of the universe remains the same or increases, never decreases, in any spontaneous process.

45:20

🔑 Boltzmann's Formula for Entropy

This section introduces Boltzmann's formula for entropy, which provides a microscopic interpretation of entropy in terms of the number of microscopic arrangements (Ω) that correspond to a given macroscopic state. The formula S = k log Ω is discussed, where k is Boltzmann's constant. The paragraph connects the macroscopic concept of entropy with the underlying microscopic physics of particle arrangements and probabilities.

50:21

🎯 Entropy as a Measure of Disorder

The paragraph concludes with a discussion on the nature of entropy as a measure of disorder in a system. It explains that entropy increases when a system moves from a state of lower probability to a state of higher probability, which is more disordered. The Second Law of Thermodynamics is described as a statistical law that dictates the direction of natural processes based on the number of microscopic arrangements available to the system.

Mindmap

Keywords

💡Carnot Engine

The Carnot engine is a theoretical heat engine that is presented as the most efficient engine possible. It operates on a reversible cycle known as the Carnot cycle, consisting of two isothermal and two adiabatic processes. In the video, the Carnot engine's efficiency is discussed in the context of the Second Law of Thermodynamics and is used to illustrate the principle that no real engine can surpass its efficiency.

💡Efficiency

Efficiency in the context of the Carnot engine refers to the ratio of work done by the engine to the heat energy taken in from the high-temperature reservoir. It is a measure of how effectively an engine converts heat into work. The video explains that the Carnot engine has a maximum theoretical efficiency, which is a fundamental concept in thermodynamics.

💡Second Law of Thermodynamics

The Second Law of Thermodynamics is a fundamental principle stating that the total entropy of an isolated system can never decrease over time, and is constant if and only if all processes are reversible. In the video, it is discussed in relation to the Carnot engine's efficiency and the concept of entropy, highlighting that natural processes tend to move towards a state of increased disorder.

💡Entropy

Entropy is a thermodynamic property that measures the degree of disorder or randomness in a system. It is a central concept in the video, where it is used to explain why certain processes occur spontaneously and others do not. The video also connects entropy to the microscopic states of a system through Boltzmann's formula, providing a statistical interpretation of entropy.

💡Reversible Process

A reversible process is one that can be reversed by infinitesimally small changes in the conditions of the system. In the context of the video, the Carnot cycle is described as a reversible process, emphasizing that such processes are idealized and occur without dissipation of energy, thus representing the maximum possible efficiency.

💡Irreversible Process

An irreversible process is one that cannot return to its initial state without adding new energy to the system. The video contrasts irreversible processes with reversible ones, noting that real-world processes are often irreversible and result in an increase in the total entropy of the universe, in accordance with the Second Law of Thermodynamics.

💡Adiabatic Process

An adiabatic process is one in which no heat is exchanged between the system and its surroundings. In the Carnot cycle, as described in the video, there are two adiabatic stages where the gas expands or is compressed without any heat transfer, leading to a change in temperature due to work done on or by the gas.

💡Isothermal Process

An isothermal process is a thermodynamic process in which the temperature of the system remains constant. The video describes the isothermal expansion and compression stages of the Carnot cycle, where heat is absorbed or released by the gas at a constant temperature, resulting in work done by or on the gas.

💡Boltzmann's Formula

Boltzmann's formula for entropy is a statistical expression that relates the entropy of a system to the number of microscopic configurations (Ways) that correspond to a given macroscopic state. In the video, it is used to explain the statistical nature of entropy and why systems tend toward increased disorder, as higher entropy states correspond to a greater number of possible microscopic arrangements.

💡Heat Reservoir

A heat reservoir, also known as a heat bath, is a system with a large heat capacity compared to the system of interest, such that the temperature of the reservoir remains constant during heat exchange. In the video, the Carnot engine exchanges heat with two temperature-reservoirs, maintaining their temperatures T1 and T2, which are critical for the calculation of the engine's efficiency.

💡Thermodynamic Cycle

A thermodynamic cycle is a series of processes through which a system goes to return to its initial state. The Carnot cycle, as discussed in the video, is an idealized thermodynamic cycle consisting of four reversible processes, which is used to define the maximum possible efficiency for converting heat into work.

Highlights

The Carnot engine is described as an idealized heat engine that operates on a reversible cycle between two temperature reservoirs.

The efficiency of the Carnot engine is defined as the work done divided by the heat energy taken in from the high-temperature reservoir.

Carnot's theorem claims no engine can exceed the efficiency of a Carnot engine operating between the same two temperatures.

The Second Law of Thermodynamics is introduced as a postulate stating it's impossible to transfer heat from a colder to a hotter body without any other effects.

Entropy is introduced as a state function that remains constant in a cyclic process, with its change defined as the heat added divided by the temperature.

The concept of reversible processes is explained, where every step of the Carnot cycle can be reversed to return to the initial state.

Entropy is shown to be a measure of the number of microscopic configurations that correspond to a given macroscopic state.

Boltzmann's constant is used to relate the microscopic definition of entropy to its thermodynamic definition.

The Second Law of Thermodynamics is discussed in terms of the increase of entropy for the universe in any spontaneous process.

An example of two water masses at different temperatures mixing to reach a common temperature is used to illustrate entropy increase.

The concept of free expansion of a gas is explored, showing that the entropy of an isolated system increases when the gas expands into a vacuum.

Boltzmann's formula for entropy, S = k log Ω, is derived, where Ω is the number of microstates corresponding to a macrostate.

The statistical interpretation of entropy is explained, where higher entropy corresponds to a greater number of possible microstates.

The arrow of time is discussed in the context of entropy, explaining why certain processes occur in one direction and not the reverse.

The practical implications of the Second Law of Thermodynamics are highlighted, including the operation of refrigerators and the natural tendency toward disorder.

The concept of local entropy decrease is acknowledged, with the caveat that overall, the entropy of the universe does not decrease.

The transcript concludes with a comprehensive understanding of why the Second Law of Thermodynamics leads to the observed natural tendencies in systems.

Transcripts

Browse More Related Video

Carnot Engine

The Second Law of Thermodynamics: Heat Flow, Entropy, and Microstates

Carnot efficiency 2: Reversing the cycle | Thermodynamics | Physics | Khan Academy

Entropy Change For Melting Ice, Heating Water, Mixtures & Carnot Cycle of Heat Engines - Physics

23. The Second Law of Thermodynamics and Carnot's Engine

Entropy intuition | Thermodynamics | Physics | Khan Academy

Related Tags

Thermodynamics Carnot Engine Efficiency Entropy Second Law Heat Transfer Statistical Mechanics Energy Conservation Reversible Processes Microstates