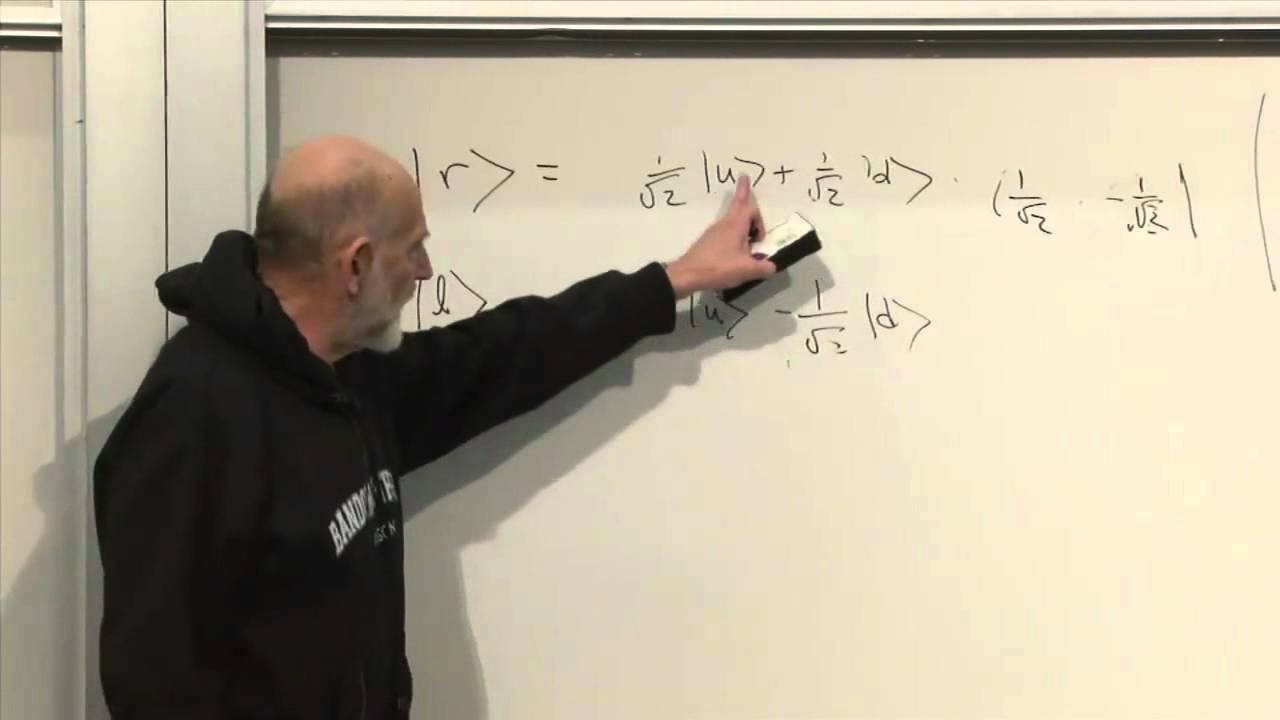Lecture 8 | Quantum Entanglements, Part 1 (Stanford)
TLDRThe video script discusses the concept of density matrices in quantum mechanics, which describe the probability distribution of a quantum system when the exact state is unknown. The lecturer explains that density matrices are a generalization of the probability postulate and are crucial for systems that may have been prepared in various states. They delve into the mathematical representation of density matrices, their properties, and how they relate to the concept of entropy as a measure of ignorance or knowledge about a system's state. The script also touches on the evolution of quantum states over time, emphasizing the role of unitary operators and the importance of maintaining logical relationships between states. The lecturer introduces the concept of entanglement, explaining how it leads to a mixed state for subsystems even when the combined system is in a pure state. The summary concludes with a brief mention of the Schrödinger equation, which governs how quantum states evolve over time, and its significance in quantum mechanics.
Takeaways
- 📈 The density matrix is a mathematical tool used in quantum mechanics to describe the state of a quantum system when the preparation is not known with certainty, generalizing the probability postulate.
- ☕️ In situations where there is no knowledge about the system's preparation, the density matrix is proportional to the identity matrix, representing a state of maximum uncertainty.
- 🧬 The trace of the density matrix, which is the sum of its diagonal elements, is always equal to one, reflecting the conservation of probability in quantum systems.
- 🌐 The density matrix is Hermitian, meaning its eigenvalues are real and represent the probabilities of finding the system in corresponding eigenstates.
- 🔍 When the system is in a pure state, the density matrix is the projection operator onto that state, allowing for the calculation of expectation values for measurements.
- 🌀 Entropy, a measure of the degree of ignorance about a system, is defined for a probability distribution and is related to the density matrix, peaking at log(n) for a uniform distribution over n states.
- 🤝 Entanglement is a quantum phenomenon where the state of one subsystem cannot be described independently of the state of another subsystem, even when the two subsystems are separated.
- 🧬 For a system composed of two entangled parts, the general state can be described by a sum over the product of the states of each part, and the normalization condition requires the sum of the probabilities to equal one.
- 📚 The expectation value of an observable for a subsystem in an entangled system can be calculated by summing over the states of the other subsystem, which remains passive during the measurement.
- ⏱️ The time evolution of quantum states is governed by unitary operators to ensure that the inner products between states remain invariant, reflecting the conservation of probability and the physical reality of the state.
- 🎓 The Hamiltonian operator, which generates the time evolution of quantum states, is Hermitian and has real eigenvalues that correspond to the energy levels of the system.
Q & A
What is the density matrix in quantum mechanics?
-The density matrix is a mathematical tool used in quantum mechanics to describe the state of a quantum system when the preparation of the system is not perfectly known. It generalizes the concept of a wave function (used for a definite state) to include probabilities for a system to be in different states.
How is the density matrix related to the probability distribution in classical physics?
-The density matrix is the quantum analog of the probability distribution in classical physics. While classical states have a probability distribution in phase space or coordinate space, the density matrix encapsulates the probabilities for different quantum states.
What is the significance of the trace of the density matrix?
-The trace of the density matrix, which is the sum of its diagonal elements, is always equal to one. This represents the conservation of probability, ensuring that the total probability across all possible states sums up to certainty.
What does it mean if the density matrix has all equal eigenvalues?
-If the density matrix has all equal eigenvalues, it signifies a state of maximum uncertainty or 'complete ignorance' about the system's state. This corresponds to a uniform probability distribution across all possible states.
What is the difference between a pure state and a mixed state in quantum mechanics?
-A pure state is described by a single wave function, indicating a definite state of the system. In contrast, a mixed state is described by a density matrix with more than one non-zero eigenvalue, which implies a lack of complete knowledge about the system's state, often due to it being in a superposition of states.
How does the concept of entropy relate to the density matrix?
-Entropy, in the context of quantum mechanics, is a measure of the uncertainty or the amount of information needed to describe a quantum system. It is calculated from the density matrix and is zero for a pure state, indicating complete knowledge, and increases with uncertainty, reaching a maximum when all states are equally probable.
What is entanglement in quantum mechanics?
-Entanglement is a quantum phenomenon where two or more particles become correlated in such a way that the state of one particle cannot be described independently of the state of the other, even when the particles are separated by large distances.
How does the expectation value of an observable relate to the density matrix?
-The expectation value of an observable in quantum mechanics, when the system is not in a pure state, is calculated using the density matrix. It is found by taking the trace of the product of the density matrix and the operator representing the observable.
What is the role of the Hamiltonian in the time evolution of a quantum system?
-The Hamiltonian, denoted by H, is a Hermitian operator that represents the total energy of the system. It governs the time evolution of the quantum state through the Schrödinger equation, ensuring that the logical relationships between states are maintained with time.
How does the principle of unitarity relate to the time evolution of quantum states?
-Unitarity is the principle that the time evolution of a quantum system is governed by unitary operators, which preserve the inner product of state vectors. This ensures that probabilities are conserved, and the distinctions between states, including orthogonality, are maintained over time.
What does the Schrödinger equation describe?
-The Schrödinger equation describes how the quantum state of a system changes with time. It is a fundamental equation in quantum mechanics that, when applied with a suitable Hamiltonian, provides the time-dependent behavior of the wave function or state vector of a quantum system.
Outlines
😀 Introduction to Density Matrix and Quantum States
The paragraph introduces the concept of the density matrix, which is a tool used in quantum mechanics to describe the probabilities of a quantum system's state. It explains that the density matrix generalizes the state vector and is particularly useful when the preparation of a system is unknown. The speaker uses the example of an electron's spin prepared by a magnetic field to illustrate the concept and touches on the idea of a mixed state versus a pure state.
🧐 Density Matrix as a Quantum Analog of Probability Distribution
This section delves deeper into the density matrix, comparing it to classical probability distributions and emphasizing its role as a quantum analog. The importance of the trace of the density matrix, which must equal one, reflecting the sum of probabilities, is highlighted. The properties of the density matrix as a Hermitian operator with real, non-negative eigenvalues are also discussed, as well as the concept of a mixed state versus a pure state.
🤔 Calculation of Expectation Values Using Density Matrix
The paragraph explains how to calculate expectation values, or average values, of observables in quantum mechanics using the density matrix. It outlines the process of taking the trace of the product of the density matrix and the observable, and how this trace is invariant under changes of basis. The calculation is illustrated using a simple case where the observable is a projection operator.
📚 Entropy and Probability Distribution in Quantum States
The concept of entropy in the context of quantum mechanics is introduced, defining it as a measure of the degree of ignorance or knowledge about a quantum system. The relationship between entropy, probability distribution, and the density matrix is explored, with examples provided to illustrate the calculation of entropy and its implications for the understanding of quantum states.
🌀 Entanglement and Composite Quantum Systems
The paragraph discusses entanglement in quantum mechanics, focusing on how the state of a composite system composed of two parts can be described. It explains the multiplication of state spaces for subsystems and how the general state of a combined system can be written as a sum over the product of coefficients and state vectors for each subsystem.
🔍 Observables and Subsystem Density Matrices
This section explores how to calculate the expectation value of an observable that is associated with one subsystem of a larger quantum system. The process involves constructing a bra vector and using it in conjunction with the observable and the state vector of the combined system. The role of the observable in 'ignoring' one subsystem and only affecting the other is also highlighted.
🚫 Subsystem States and Density Matrix Formalism
The paragraph examines the states of subsystems within a larger quantum system, particularly when the overall system is in a pure state. It explains that while the combined system can be described by a single state vector, each subsystem is generally described by a density matrix, which can be obtained by summing over the states of the other subsystem. The special case where the subsystem is also in a pure state is also discussed.
🔗 Entanglement, Pure States, and Product States
This section discusses the conditions under which a wave function can be factorized into products of functions, leading to each subsystem being in a pure state. The concept of a product state is introduced, and it is shown that the density matrix for such a state is the product of the wave functions of the individual subsystems. The entropy of the state is also calculated to demonstrate the level of entanglement.
🤓 Time Evolution of Quantum States
The paragraph addresses how quantum states evolve over time, contrasting discrete and continuous evolution. It introduces the concept that the evolution of a quantum state is governed by a linear operator, which is unitary to ensure that the logical relationships between states are maintained. The importance of orthogonality and inner products remaining invariant with time is emphasized.
🔍 Derivation of the Time Evolution Operator
The paragraph provides a derivation of the time evolution operator, starting with the assumption that the operator is unitary. By considering a small time interval and expanding the operator to first order in this interval, the conditions for the operator to be unitary are explored. The resulting equation leads to the definition of the Hamiltonian as a Hermitian operator, which represents the energy of the system.
🌟 Eigenvalues, Eigenvectors, and Energy Levels
This section discusses the eigenvalues and eigenvectors of the Hamiltonian, noting that the eigenvalues correspond to the energy levels of a quantum system. It is stated that if a system starts in an eigenstate of the Hamiltonian, it will remain in that eigenstate over time, evolving merely by a time-dependent phase factor. The relationship between energy, frequency, and the reduced Planck constant is also mentioned.
⏳ Schrodinger Equation and Time Evolution
The paragraph introduces the generalized Schrodinger equation, which describes how quantum states change with time for any system. It emphasizes the need to select an appropriate Hamiltonian for the system in question. The equation is derived from the principles of quantum mechanics, and it is shown that the state vector evolves with an angular frequency proportional to the energy.
Mindmap
Keywords
💡Density Matrix
💡Probability Distribution
💡Hermitian Operator
💡Trace
💡Eigenvalues and Eigenvectors
💡Entanglement
💡Subsystem
💡Observable
💡Schrodinger Equation
💡Hamiltonian
💡Entropy
Highlights
The density Matrix is a way of describing probabilities in quantum mechanics when the exact state of a system is not known.
If there is no knowledge about the system, the density Matrix is proportional to the unit Matrix, indicating complete randomness.
The trace of the density Matrix, which is the sum of its eigenvalues, equals one, representing the total probability.
The density Matrix is a Hermitian operator, ensuring that the probabilities are real numbers.
Eigenvalues of the density Matrix can be thought of as probabilities for different states, with the diagonal entries being real and non-negative.
In a state of complete ignorance, the system is described by a density Matrix with equal eigenvalues, each being 1/n, where n is the number of states.
The limit of maximal knowledge is a pure state, which is described by a density Matrix that is the projection onto that pure state.
The concept of entropy in quantum mechanics is a measure of the degree of ignorance or the amount of information known about a system.
Entanglement occurs when a system is composed of two or more parts and can lead to a high degree of correlation between the parts.
The expectation value of an observable in a quantum system can be calculated using the trace of the product of the density Matrix and the observable.
The singlet state of two electrons is an example of a highly entangled state, resulting in a density Matrix that is proportional to the unit Matrix.
The entropy of a system can be used to determine the purity of a state or the degree of entanglement.
The product state is a special case where the wave function can be factorized into a product of functions of each subsystem, indicating less entanglement.
The time evolution of quantum systems is governed by unitary operators, which preserve the inner product between any two states.
The Hamiltonian operator, which generates the time evolution, is Hermitian and represents the total energy of the system.
The Schrödinger equation describes how the state vector of a quantum system changes with time, with the Hamiltonian determining the evolution.
Eigenstates of the Hamiltonian remain eigenstates for all time, evolving with a phase factor that depends on the energy and time.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: