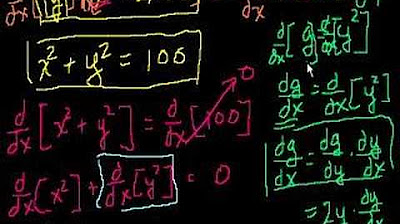dy/dx, d/dx, and dy/dt - Derivative Notations in Calculus
TLDRThis video script delves into the distinction between 'dy/dx' and 'd/dx' in the context of derivatives. It clarifies that 'dy/dx' represents the derivative of a function 'y' with respect to 'x', exemplified by the calculation of the derivative for the function 'y = x^3 + 4x^2'. In contrast, 'd/dx' is an operator that instructs to find the derivative of the enclosed expression with respect to 'x'. The script further explores implicit differentiation, differentiating with respect to various variables like 's' and 't', and concludes with a practical example involving related rates and differentiation with respect to 'y' and 't'.
Takeaways
- 📚 The main difference between dy/dx and d/dx lies in their representation and usage in calculus problems.
- 🔍 dy/dx signifies the derivative of a function, specifically y with respect to x, while d/dx represents the action of differentiating the function inside the brackets with respect to x.
- 🌟 For a function like y = x^3 + 4x, the derivative (dy/dx) is calculated as 3x^2 + 8x.
- 📝 When variables don't match, as in dy/dx = 3y^2 + 8y, it indicates the need for implicit differentiation.
- 🤔 To find the derivative of x^3 with respect to x, the result is 3x^2, but for y^3 with respect to x, it's 3y^2(dy/dx).
- 🔢 Differentiation can be done with respect to various variables, such as x, s, or t, depending on the context of the problem.
- 🕒 In related rates problems, d/dt is commonly used to denote differentiation with respect to time.
- 🧠 The process of implicit differentiation is showcased by differentiating x^5 with respect to another variable, s, resulting in 5x^4(dx/ds).
- 📊 The example of differentiating x^4 + y^3 with respect to time (d/dt) illustrates the concept of related rates in calculus.
- 📈 To find dR/dy for a function R(x, t) = x^3 + t^5, one must differentiate each term with respect to y, considering the relationship between x and y (dx/dy) and t and y (dt/dy).
Q & A
What is the main difference between 'dydx' and 'd over dx'?
-The main difference is that 'dydx' represents the derivative of a function y with respect to x, while 'd over dx' is an instruction to find the derivative of the function inside the brackets with respect to x.
If y is equal to x cubed plus 4x, what is the derivative of y with respect to x?
-The derivative of y with respect to x, denoted as dydx, is 3x squared plus 8x.
What does 'd over ds' express when differentiating with respect to a variable other than x?
-'d over ds' expresses a command to find the derivative of the function with respect to a variable s, which could be any other variable or parameter.
In the context of related rates problems, what does 'd over dt' represent?
-In related rates problems, 'd over dt' represents the differentiation with respect to time, indicating the rate of change over time.
How do you find the derivative of y cubed with respect to x?
-The derivative of y cubed with respect to x is 3y squared times dy over dx, highlighting the concept of implicit differentiation.
What is the derivative of x to the fifth power with respect to some variable s?
-The derivative of x to the fifth power with respect to s is 5x to the fourth power times dx over ds.
How do you differentiate x to the fourth power plus y cubed with respect to time?
-The derivative with respect to time is 4x cubed times dx over dt plus 3y squared times dy over dt.
In the given script, what is the process of taking the derivative of a function r with respect to y?
-The process involves replacing r with its equivalent expression, x cubed plus t to the fifth power, and then differentiating each term with respect to y, resulting in three x squared times d x over d y plus five t to the fourth power times d t over d y.
What does the expression 'd r over d y' equal to in the context of the script?
-In the context of the script, 'd r over d y' is equal to three x squared times d x over d y plus five t to the fourth times d t over d y.
How does the script help differentiate between 'dydx' as a statement and 'd over dx' as a command?
-The script clarifies that 'dydx' is used to make a statement about the derivative of a function y with respect to x, while 'd over dx' instructs to perform the action of differentiating the function inside the brackets with respect to x.
What is the significance of understanding the difference between 'dydx' and 'd over dx'?
-Understanding the difference is crucial for correctly applying the rules of differentiation, interpreting mathematical expressions, and solving calculus problems accurately.
Outlines
📚 Understanding dy/dx and d/dx
This paragraph introduces the concepts of dy/dx and d/dx in the context of derivatives. It explains that dy/dx represents the derivative of a function, denoted as y, with respect to x, while d/dx signifies a command to find the derivative of the function inside the brackets with respect to x. The video uses the function y = x^3 + 4x as an example to illustrate the difference between the two notations. It emphasizes that d/dx instructs to differentiate the expression inside the brackets (e.g., x^3 + 4x^2), resulting in the derivative 3x^2 + 8x. The explanation continues with the differentiation of y^3 with respect to x, highlighting the concept of implicit differentiation. The paragraph concludes with a discussion on differentiating with respect to other variables, such as s or t, and introduces related rates problems, differentiating x^4 + y^3 with respect to time.
🧠 Applying Derivatives: Pop Quiz and Implicit Differentiation
The second paragraph focuses on applying the concepts of derivatives learned in the first part. It presents a pop quiz to engage the viewer, asking to find the derivative of a function r, which is a function of x and t, with respect to y. The solution involves replacing r with its given expression (x^3 + t^5) and differentiating with respect to y. The derivative of x^3 with respect to y is 3x^2 multiplied by d/dx over d/dy, and the derivative of t^5 with respect to y is 5t^4 multiplied by d/dt over d/dy. The paragraph concludes by reinforcing the understanding of the difference between dy/dx and d/dx, and the video ends with a note of hope that the content was helpful.
Mindmap
Keywords
💡Derivatives
💡dy/dx
💡d/dx
💡Power Rule
💡Implicit Differentiation
💡Related Rates
💡dx/dt
💡dy/dt
💡Variable
💡Rate of Change
💡Function
Highlights
The video discusses the difference between dydx and d over dx in the context of derivatives.
dydx represents the derivative of a function y with respect to x.
d over dx indicates the operation of finding the derivative of the function inside the brackets with respect to x.
For a function y = x^3 + 4x, its derivative dydx is 3x^2 + 8x.
The expression d y over dx is equivalent to taking the derivative of y with respect to x.
The derivative of x^3 with respect to x is 3x^2.
When differentiating y^3 with respect to x, the result is 3y^2 times dy over dx, which is an example of implicit differentiation.
Differentiation with respect to another variable, such as s, is denoted as d over ds.
The derivative of x^5 with respect to s is 5x^4 times dx over ds.
In related rates problems, differentiation with respect to time t is represented as d over dt.
When differentiating x^4 + y^3 with respect to time, the result includes terms involving dx/dt and dy/dt.
The process of implicit differentiation involves differentiating an expression without explicitly stating the variable of differentiation.
The video provides a clear explanation of how to differentiate polynomial functions using the power rule.
The concept of related rates is introduced, which involves differentiating with respect to time or other variables.
The video uses the example of r = x^3 + t^5 to demonstrate how to find the derivative with respect to another variable, y.
The derivative of a composite function involves applying the chain rule, as shown in the example with r and its components.
The video emphasizes the importance of understanding the difference between stating a derivative (dydx) and the operation of differentiation (d over dx).
The video concludes with a pop quiz to test the viewer's understanding of the concepts discussed.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: