The Logistic Equation and Models for Population - Example 1, part 1

patrickJMT
17 Oct 201007:04
EducationalLearning
32 Likes 10 Comments

TLDRIn this video, the host delves into an example related to the logistic equation, a model used to represent population growth. They begin with a scenario where biologists stock a lake with 500 fish and determine a carrying capacity of 10,000 fish. Knowing that the fish population tripled in the first year, the host uses the logistic equation to derive a formula that predicts the population size after T years. The logistic equation is a separable differential equation, which, after integration, provides a formula involving the carrying capacity, initial population, and a constant K. By substituting the known values and setting the population at one year to 1,500 fish, the host solves for K, which is crucial for the formula. They then simplify the formula to express the population at time T in terms of the natural logarithm, resulting in a clean and accurate model for population dynamics. The video concludes with a promise to address in a follow-up video how long it will take for the population to reach 4,000 fish.

Takeaways
  • 📈 The logistic equation is used to model population growth and is represented as dP/dt = r * P * (1 - P/K), where r is the growth rate, P is the population, and K is the carrying capacity.
  • 🐟 In the given example, a lake is stocked with 500 fish, and the carrying capacity is determined to be 10,000 fish.
  • 🔄 The population tripled in the first year, indicating a significant growth rate for the fish population in the lake.
  • 🧮 The logistic equation is a separable differential equation, which can be solved to find the population at time T.
  • 📚 The formula for the population at time T is derived as P(T) = K / (1 + (K - P0) / P0 * e^(-rT)), where P0 is the initial population.
  • ⏱ To find the constant 'r' (growth rate), the population after one year is used, which is 1500 fish in this case.
  • 🔍 The value of 'a' is calculated using the carrying capacity and the initial population, resulting in 'a' = (K - P0) / P0.
  • 🧮 By substituting the known values into the logistic equation and solving for 'r', the growth rate can be determined.
  • 🔢 The natural logarithm (ln) is used to isolate the variable 'r' in the logistic equation, leading to a solution for the growth rate.
  • 📉 The negative growth rate (-r) is then used to find the population at any given time T using the derived formula.
  • 🌿 The final population formula is simplified to P(T) = 10,000 / (1 + 19 * (17/57)^T), which can be used to predict the fish population at any time T.
  • 📅 Part B of the video will focus on determining the time it takes for the population to reach a specific target, such as 4,000 fish.
Q & A

  • What is the logistic equation used for?

    -The logistic equation is used to model population growth, taking into account the carrying capacity of the environment.

  • What does the variable 'P' represent in the logistic equation?

    -In the logistic equation, 'P' represents the population at a certain time 'T'.

  • What is the carrying capacity denoted by in the logistic equation?

    -The carrying capacity is denoted by 'K' in the logistic equation, which is the maximum population size that the environment can sustain indefinitely.

  • What is the constant 'K' in the logistic equation?

    -The constant 'K' in the logistic equation is a constant of proportionality that relates the change in population to the current population size.

  • How many fish were initially stocked in the lake in the given example?

    -In the given example, 500 fish were initially stocked in the lake.

  • What was the carrying capacity of the lake in the example?

    -The carrying capacity of the lake in the example was determined to be 10,000 fish.

  • What happened to the fish population in the first year according to the example?

    -The fish population tripled during the first year, reaching a population of 1,500 fish.

  • How was the formula for the population at time 'T' derived?

    -The formula for the population at time 'T' was derived by integrating both sides of the logistic equation, which is a separable differential equation.

  • What is the value of 'a' used in the logistic growth formula?

    -The value of 'a' is calculated as the carrying capacity 'K' minus the initial population, divided by the initial population.

  • How was the constant 'K' determined in the example?

    -The constant 'K' was determined by using the information that the population tripled in the first year and solving the logistic equation for 'K'.

  • What is the final form of the population formula at time 'T' after solving for 'K'?

    -The final form of the population formula at time 'T' is P(T) = 10,000 / (1 + 19 * (17/57)^T), where 'T' is the number of years since the initial population.

  • Why is it recommended to leave the natural logarithm in the formula instead of converting it to a decimal?

    -Leaving the natural logarithm in the formula allows for the logarithm to cancel out when plugging values into the formula, resulting in a cleaner and more accurate calculation.

Outlines
00:00
📚 Introduction to the Logistic Equation and Population Growth Model

This paragraph introduces the logistic equation, which is used to model population growth. It explains the basic formula of the logistic equation, where the change in population (P) with respect to time (T) is proportional to the carrying capacity (K) and the current population. The video sets up a scenario where a lake is stocked with 500 fish, with a carrying capacity of 10,000 fish. It is mentioned that the population triples in the first year, and the goal is to find an expression for the population size after T years. The paragraph concludes with the logistic equation's solution, which is a formula involving the carrying capacity, initial population, and time.

05:00
🧮 Deriving the Population Formula and Solving for the Constant K

The second paragraph delves into the process of deriving the formula for the population at time T using the logistic equation. It starts by defining the carrying capacity (K) as 10,000 and calculating the value of 'a' using the initial population of 500 fish. The paragraph then describes how to use the logistic growth formula to find the population at a future time T. The key step involves solving for the constant K using the information that the fish population tripled in the first year. By substituting T=1 year into the formula and setting it equal to the new population (1500 fish), the video guides through the algebraic manipulation to isolate and solve for K. The process involves taking the natural logarithm to solve for K, which is left as an intermediate step for the next part of the video.

Mindmap
Keywords
💡Logistic Equation
The logistic equation is a mathematical model used to describe population growth in an environment where the growth rate is limited by the carrying capacity of the environment. In the video, it is used to model the growth of a fish population in a lake, with the change in population over time being proportional to the difference between the carrying capacity and the current population size.
💡Carrying Capacity (K)
Carrying capacity refers to the maximum population size that an environment can sustain indefinitely, given the food, habitat, water, and other necessities available in the environment. In the video, the carrying capacity of the lake is given as 10,000 fish, which is the limit to how many fish the lake can support.
💡Population Growth
Population growth is the increase in the number of individuals in a population over time. The video discusses how the logistic equation can be used to model this growth, particularly in the context of a fish population that is initially stocked and then grows over time.
💡Constant of Proportionality (little K)
The constant of proportionality, often denoted as 'little K' in the logistic equation, is a factor that determines the rate at which the population grows. It is a key parameter in the logistic model and is used to calculate the change in population size over time.
💡Initial Population
The initial population refers to the number of individuals in a population at the start of a study or observation period. In the video, the initial population of fish in the lake is 500, which serves as the starting point for the logistic growth model.
💡Separable Differential Equation
A separable differential equation is a type of differential equation where the terms involving the dependent and independent variables can be separated, making it easier to solve. The logistic equation is identified as separable in the video, which allows for integration and the derivation of a formula for the population at any time T.
💡Natural Logarithm (ln)
The natural logarithm, denoted as 'ln', is the logarithm to the base 'e', where 'e' is an irrational number approximately equal to 2.71828. In the video, the natural logarithm is used to solve for the constant 'K' in the logistic equation, which is essential for determining the population size at any given time.
💡Exponential Function
An exponential function is a mathematical function of the form f(x) = a * b^x, where 'a' and 'b' are constants and 'x' is the variable. In the logistic equation, the exponential function e^(-little K * T) is used to model the growth of the population, showing how the population changes over time.
💡Integration
Integration is a mathematical process that is the reverse of differentiation and can be used to find the accumulated value of a function over an interval. In the video, integration is used to solve the logistic differential equation and derive the formula for the population at time T.
💡Time (T)
Time, denoted as 'T' in the logistic equation, represents the independent variable, which is the number of years or time units that have passed since the initial population measurement. The video uses 'T' to calculate the population size at different points in time based on the logistic growth model.
💡Solving for K
Solving for 'K' involves finding the value of the constant of proportionality in the logistic equation that best fits the observed data. In the video, the presenter uses the information that the fish population tripled in the first year to solve for 'K', which is a critical step in applying the logistic model to the population growth scenario.
Highlights

The logistic equation is used to model population growth, representing the change in population with respect to time.

The logistic equation includes a constant of proportionality (little K) and the carrying capacity (capital K).

Biologists stock a lake with 500 fish and determine the carrying capacity to be 10,000 fish.

The number of fish triples during the first year, indicating logistic growth.

An explicit solution to the logistic differential equation is derived by integrating both sides.

The formula for the population at time T is derived as K / (1 + a * e^(-KT)) where a = (K - initial population) / initial population.

The carrying capacity K is 10,000 and the initial population is 500, so a = (10,000 - 500) / 500 = 19.

The population at time T is given by P(T) = 10,000 / (1 + 19 * e^(-KT)) where K is a constant to be determined.

The population triples to 1,500 in the first year, which is used to solve for the constant K.

Solving for K involves taking the natural logarithm and simplifying the equation.

The final formula for the population at time T is P(T) = 10,000 / (1 + 19 * (17/57)^T).

Leaving the natural logarithm in the formula simplifies calculations and provides a more accurate result.

Part B of the video will determine how long it takes for the population to reach 4,000.

The logistic equation provides a nice formula for modeling population growth over time.

The video demonstrates the process of deriving and solving the logistic equation step by step.

The carrying capacity and initial population are key parameters in the logistic equation.

The video provides an example of applying the logistic equation to model fish population growth in a lake.

The derived formula can be used to predict the population at any future time T.

Transcripts

Browse More Related Video

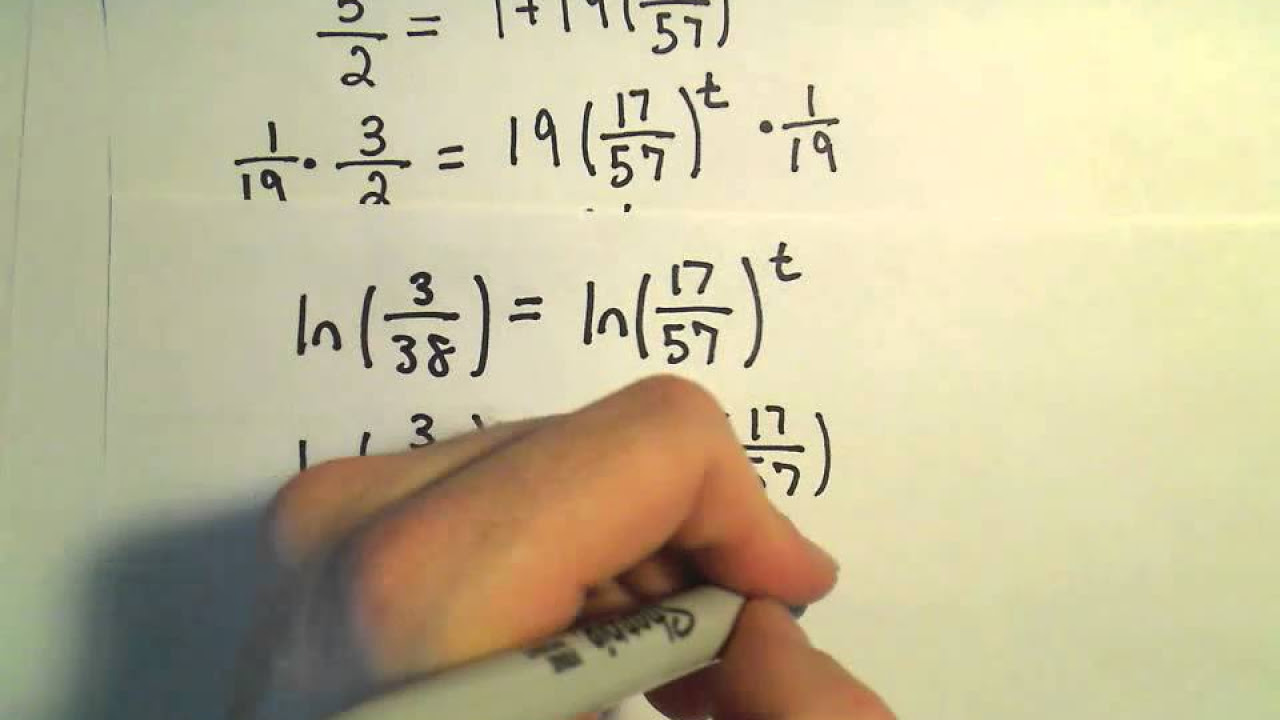
The Logistic Equation and Models for Population - Example 1, part 2

The Logistic Equation and the Analytic Solution

Solving the logistic differential equation part 2 | Khan Academy

Logistic Differential Equation (general solution)

AP Calc BC: How to Solve a Logistic Growth Application Problem

Solving the logistic differential equation part 1 | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Logistic EquationPopulation GrowthMathematical ModelingBiological EcologyDifferential EquationsCarry CapacityFish PopulationEnvironmental ScienceGrowth ConstantNatural LogarithmModeling Techniques