Solving the logistic differential equation part 1 | Khan Academy
TLDRIn the video script, the presenter delves into solving the logistic differential equation, a model for population growth that accounts for limited resources. They begin by reviewing constant solutions, such as the scenario where the population is zero or at the maximum sustainable level, where the rate of change is zero. The presenter then explores the possibility of a non-constant solution where the population starts below the maximum sustainable level. They introduce the concept of the separable differential equation and proceed to solve it using partial fraction expansion. The process involves taking the anti-derivative of both sides with respect to time, which leads to the natural logarithm of the population size and its relation to the carrying capacity. The presenter successfully simplifies the equation, bringing the audience closer to finding the analytic expression for the population over time. The video concludes with the promise of continuing the solution in the next installment, leaving viewers intrigued and eager for more.
Takeaways
- 📐 The logistic differential equation models population growth with a carrying capacity K, where the growth rate decreases as the population size N approaches K.
- ⏹ At N=0, the rate of population change is zero, as there are no individuals to reproduce, which is consistent with real-world scenarios.
- 🔄 When the population N equals the carrying capacity K, the growth rate is also zero, leading to a constant solution where the population remains at its maximum sustainable level.
- 📈 For initial conditions where N is between 0 and K, the rate of change of the population is proportional to N, leading to growth that approaches the carrying capacity asymptotically.
- 🧩 The logistic equation is separable, allowing for an analytical solution by separating variables and integrating both sides with respect to time t.
- ✅ The partial fraction expansion technique is used to simplify the equation into two fractions, which can be more easily integrated.
- 📉 The anti-derivatives of 1/N and ln|N| are used to find the integral of the separated equation, with the latter being a natural logarithm whose derivative is 1/N.
- 🔀运用链式法则(Chain Rule)来找到复合函数的导数,这对于解决涉及N和时间t的表达式是至关重要的。
- 🚫 Assumption is made that N(t) is always between 0 and K, ensuring that terms involving N remain positive and valid within the logistic model's context.
- 🔢 The integration with respect to t results in an equation involving natural logarithms of N and (1 - N/K), leading to a general form of the solution for N(t).
- 🔄 The process involves finding constants A and B through partial fraction decomposition, where A/N + B/(1 - N/K) equals 1/N * (1 - N/K).
- ⏩ The final solution for N(t) is approached but will be completed in a subsequent video, highlighting the iterative and stepwise nature of solving differential equations.
Q & A
What is the logistic differential equation?
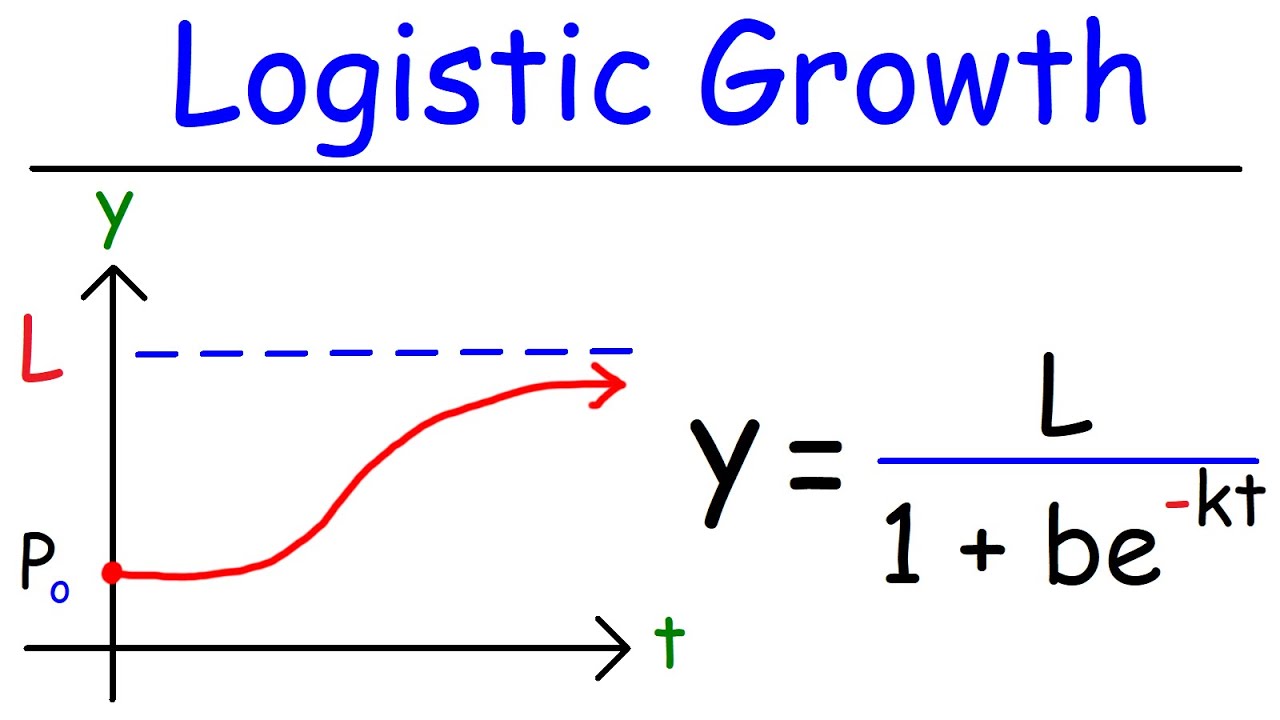
-The logistic differential equation is a mathematical model used to describe population growth when the growth rate is not constant but depends on the size of the population. It is often used to model growth where there is a limited carrying capacity, such as in an environment that can only sustain a certain maximum population size.
What are the two constant solutions for the logistic differential equation mentioned in the script?
-The two constant solutions mentioned are: 1) N(t) = 0, which represents a scenario where the population remains at zero, as there are no individuals to reproduce. 2) N(t) = K, which represents a scenario where the population remains at the maximum sustainable size K, as the growth rate becomes zero once the population reaches this size.
What is the significance of the constant r in the logistic differential equation?
-The constant r in the logistic differential equation represents the intrinsic growth rate of the population. It is a positive constant that, when multiplied by the population size N, gives the number of individuals able to reproduce at any given time.
How does the logistic differential equation account for environmental carrying capacity?
-The logistic differential equation accounts for environmental carrying capacity through the term '1 - N/K'. As the population size N approaches the carrying capacity K, the term '1 - N/K' approaches zero, which in turn reduces the growth rate of the population, preventing it from exceeding the environment's carrying capacity.
What is a Malthusian mindset in the context of population growth?
-A Malthusian mindset refers to the idea that population growth can outstrip the means of subsistence, leading to a crisis. It is named after Thomas Malthus, who argued that population growth tends to increase geometrically (exponentially), while the food supply tends to increase arithmetically, which could lead to a shortage of resources.
What is the process of partial fraction expansion and why is it used in the script?
-Partial fraction expansion is a technique used in mathematics to break down a complex fraction into simpler fractions, typically when dealing with rational functions. In the script, it is used to simplify the expression for further integration and to make it easier to find the anti-derivative required to solve the logistic differential equation.
What is the significance of the natural logarithm in solving the logistic differential equation?
-The natural logarithm is used to find the anti-derivatives of the terms '1/N' and '1/(1 - N/K)'. Knowing the anti-derivatives allows the integration of these terms with respect to time, which is a crucial step in solving the logistic differential equation and finding the function N(t).
What is the role of the constant C in the general solution of the logistic differential equation?
-The constant C in the general solution represents an arbitrary constant of integration, which arises when integrating differential equations. It accounts for the initial conditions or the specific path the solution takes, and different values of C will yield different particular solutions to the logistic differential equation.
What is the assumption made about N(t) in the script?
-The assumption made about N(t) in the script is that it is always less than K and greater than zero (N(t) < K and N(t) > 0). This assumption ensures that the population size remains within the bounds of the environment's carrying capacity and above zero.
How does the logistic differential equation model population growth that is more consistent with a Malthusian mindset?
-The logistic differential equation models population growth that accounts for limited resources, which is more consistent with a Malthusian mindset. It incorporates a carrying capacity K, which represents the maximum population size that the environment can sustain, thus preventing unlimited exponential growth.
What is the next step after finding the anti-derivatives in the logistic differential equation?
-The next step after finding the anti-derivatives is to solve for N(t) by integrating both sides of the equation with respect to time and applying any given initial conditions to find the particular solution that fits the specific population scenario being modeled.
Outlines
📐 Introduction to the Logistic Differential Equation
The video begins with an attempt to solve the logistic differential equation, which models population growth with a carrying capacity. The presenter reviews constant solutions, such as N(t) = 0 (no growth) and N(t) = K (maximum sustainable population). The focus then shifts to the possibility of a dynamic solution where the initial population is between these two constants. The logistic equation is identified as a separable differential equation, and the presenter starts to manipulate it to find an analytic expression for N(t), which would represent a more realistic growth model.
🔍 Partial Fraction Expansion and Integration
The presenter continues by separating the logistic differential equation and performing a partial fraction expansion to simplify the equation. This step involves finding constants A and B such that A/N + B/(1 - N/K) equals the right side of the equation. Through algebraic manipulation, A is determined to be 1 and B is found to be 1/K. The equation is then rewritten in a more integrable form. The presenter highlights the importance of recognizing the integral of 1/N and using the chain rule to find the derivative of the natural logarithm of (1 - N/K) with respect to N, which is crucial for the next steps in solving the differential equation.
🧮 Integration and Solution Assumptions
The video script outlines the process of taking the anti-derivative of both sides of the equation with respect to time, t. The presenter assumes N(t) is always positive and less than the carrying capacity K, which simplifies the natural logarithms involved. By integrating, the presenter arrives at an equation involving the natural logarithm of the absolute value of N and (1 - N/K), equal to a constant plus r times t. The presenter then subtracts a constant (C1) from both sides to isolate the natural logarithm terms, leading to a general form of the solution. The video concludes with a teaser for the next video, where the presenter is eager to finalize the solution for N(t).
Mindmap
Keywords
💡Logistic Differential Equation
💡Constant Solutions
💡Partial Fraction Expansion
💡Anti-Derivative
💡Natural Logarithm
💡Separable Differential Equation
💡Rate of Change
💡Carrying Capacity (K)
💡Asymptote
💡Initial Condition
💡Malthusian Mindset
Highlights
The logistic differential equation is being explored for solutions.
Constant solutions for N(t) = 0 and N(t) = K are identified, representing no population growth and maximum sustainable population, respectively.
The scenario where the initial condition is between zero and the environmental carrying capacity is considered.
The rate of change of the population is found to be proportional to N and approaches zero as N approaches the carrying capacity K.
A potential solution is hypothesized where the population asymptotically approaches the carrying capacity K.
The differential equation is recognized as separable, simplifying the process of finding N(t).
Partial fraction expansion is used to simplify the equation and find an expression for the anti-derivative.
The integration of 1/N and 1/(1 - N/K) with respect to N is performed to find the anti-derivatives.
The natural logarithm of the absolute value of N and (1 - N/K) are identified as the anti-derivatives.
Integration with respect to time t is carried out to progress towards finding N(t).
The assumption is made that N(t) is always between zero and K, ensuring the natural logarithm arguments are positive.
An arbitrary constant C is introduced to account for the integration constant.
The process of solving for N(t) is continued in the next video due to the complexity and length of the explanation.
The approach to solving the logistic differential equation is a blend of differential calculus, algebra, and partial fraction decomposition.
The potential application of the logistic differential equation in modeling population growth with environmental constraints is discussed.
The solution process is detailed, emphasizing the step-by-step mathematical operations and assumptions made.
The video concludes with a teaser for the next part of the solution, maintaining viewer engagement and interest.
Transcripts
Browse More Related Video
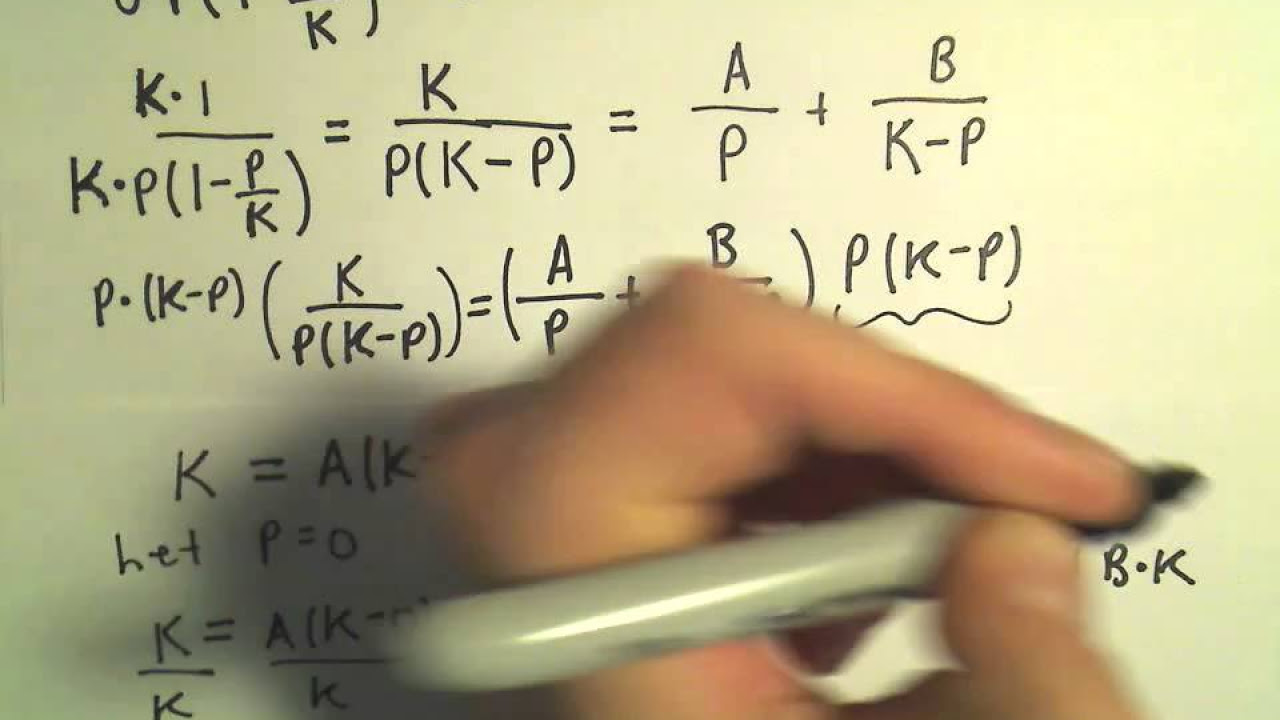
The Logistic Equation and the Analytic Solution

The Logistic Equation and Models for Population - Example 1, part 1

Modeling population with simple differential equation | Khan Academy

Solving the logistic differential equation part 2 | Khan Academy
Logistic Growth Function and Differential Equations

Logistic Differential Equation (general solution)
5.0 / 5 (0 votes)
Thanks for rating: