Logistic Differential Equation (general solution)
TLDRThe video script presents a detailed explanation of the logistic differential equation, a mathematical model used to describe population growth. It emphasizes the concept of the carrying capacity (m), which is the maximum population size an environment can sustain. The script walks through the process of solving the logistic differential equation by separating variables and integrating both sides. It introduces the use of partial fractions to handle complex fractions and demonstrates the integration steps leading to the logistic growth equation in function notation, P(t). The video also shows how to determine the constant C in the logistic equation using the initial population, P(0), and the carrying capacity, m. The final logistic growth equation is P(t) = m / (1 + C * e^(-Kt)), where C is derived from the initial conditions. This summary encapsulates the key points of the video, providing a clear and concise understanding of the logistic differential equation and its application in modeling population dynamics.
Takeaways
- 📐 The logistic differential equation models population growth, taking into account the carrying capacity (m), which is the maximum population size the environment can sustain.
- 🔄 The rate of population change is proportional to both the current population (P) and the factor (1 - P/m), reflecting how population growth slows as it approaches the carrying capacity.
- 🧮 The equation can be solved by separating variables and integrating both sides, which involves dealing with complex fractions and partial fraction decomposition.
- 📈 The solution process involves integrating terms like 1/P and 1/(M - P), which requires combining fractions and simplifying the integral expressions.
- 🌱 The integration results in the natural logarithm of the ratio of current population to the difference between carrying capacity and current population, which is then set equal to a constant times time (KT) plus another constant (C1).
- ➗ To isolate P, the reciprocal of both sides of the equation is taken, which simplifies the equation and makes it easier to solve for P.
- 🔗 The final form of the logistic growth equation is P = M / (1 + C4 * e^(-KT)), where C4 is a constant that depends on the initial population and carrying capacity.
- ⚖️ The constant C4 can be found using the initial population (P0), by rearranging the logistic equation to solve for C4 in terms of P0 and M.
- 📉 The logistic model shows that as the population size grows, the growth rate decreases, which is different from the exponential growth model where the growth rate remains constant.
- 🌟 The logistic differential equation is widely used in biology, ecology, and other fields to describe the growth of populations under limited resources.
- 🔧 Understanding the logistic model is crucial for managing and predicting population dynamics, especially in the context of environmental sustainability and resource management.
Q & A
What is the logistic differential equation?
-The logistic differential equation is a model used to describe the growth of populations. It states that the rate of change of the population with respect to time is proportional to the population itself and to the factor (1 - P/M), where P is the population size and M is the carrying capacity, which is the maximum population size that the environment can sustain.
What is the carrying capacity in the logistic differential equation?
-The carrying capacity (M) in the logistic differential equation is the maximum population size that the environment can sustain indefinitely. It represents the limit on population growth due to environmental constraints.
How does the logistic differential equation account for environmental limitations?
-The logistic differential equation accounts for environmental limitations through the term (1 - P/M). As the population size (P) approaches the carrying capacity (M), the growth rate slows down, preventing the population from exceeding the carrying capacity.
What is the general form of the logistic growth equation?
-The general form of the logistic growth equation is P(t) = M / (1 + C * e^(-K * t)), where P(t) is the population size at time t, M is the carrying capacity, C is a constant, K is the growth rate constant, and e is the base of the natural logarithm.
How is the constant C determined in the logistic growth equation?
-The constant C in the logistic growth equation is determined by the initial population size (P0). It is calculated as C = M - P0 / P0, where P0 is the population size at time t=0.
What is the significance of the term e^(-K * t) in the logistic growth equation?
-The term e^(-K * t) in the logistic growth equation represents the exponential decay of the population's growth rate over time. It is a function of the growth rate constant (K) and time (t), and it ensures that the population growth slows down as the population size approaches the carrying capacity.
How does the logistic growth equation differ from the exponential growth equation?
-The logistic growth equation differs from the exponential growth equation by including a term that limits the growth rate as the population size approaches the carrying capacity. In contrast, the exponential growth equation assumes that the growth rate remains constant, leading to unbounded growth which is not sustainable in real-world scenarios.
What is the role of partial fractions in solving the logistic differential equation?
-Partial fractions are used to break down complex fractions into simpler terms that can be more easily integrated. In the context of solving the logistic differential equation, partial fractions help in integrating the term involving P and M to find the general solution for the population size over time.
What is the significance of the absolute value in the logistic growth equation?
-The absolute value in the logistic growth equation ensures that the population size remains non-negative, which is a realistic assumption since population sizes cannot be negative.
How does the logistic growth equation model the transition from exponential growth to a stable population size?
-The logistic growth equation models the transition from exponential growth to a stable population size by incorporating a factor that reduces the growth rate as the population approaches the carrying capacity. This results in an S-shaped curve, where the population grows rapidly at first, then slows down, and finally stabilizes at the carrying capacity.
What are the steps involved in solving the logistic differential equation?
-The steps involved in solving the logistic differential equation include: separating variables, integrating both sides, using partial fractions to simplify the integral, and applying integration techniques to find the general solution for the population size over time. Finally, using an initial condition (such as the initial population size) allows for the determination of the constant C and the specific solution for the population dynamics.
Outlines
🧮 Introduction to the Logistic Differential Equation
The video introduces the logistic differential equation, a model for population growth that accounts for carrying capacity. The rate of population change is proportional to the current population and a factor involving the difference between the carrying capacity (m) and the current population (P). The solution process involves separating variables and integrating both sides, with partial fractions used to handle complex fractions. The final form of the solution is expressed as an integral involving natural logarithms and is then simplified to isolate P, resulting in the logistic growth equation in terms of time (T).
📈 Solving the Logistic Differential Equation
This paragraph delves into the solution of the logistic differential equation. It explains the integration process, including handling the absolute value and the use of the cover-up method for partial fractions. The solution involves natural logarithms and exponential functions, leading to the logistic growth equation in a more explicit form. The video also demonstrates how to adjust the equation to account for an initial population (P naught), resulting in a formula for C that relates the carrying capacity, initial population, and the constant from the logistic equation.
🔢 Applying the Logistic Growth Equation
The final paragraph focuses on applying the logistic growth equation to practical scenarios. It provides a formula for determining the constant C in the logistic equation based on the initial population and carrying capacity. The video emphasizes the importance of transforming the differential equation into a recognizable form to apply this formula. It concludes with an invitation for viewers to subscribe to the channel for more content on similar topics.
Mindmap
Keywords
💡Logistic Differential Equation
💡Carrying Capacity (M)
💡Separation of Variables
💡Partial Fractions
💡Integration
💡Natural Logarithm
💡Derivative
💡Initial Population (P naught)
💡Constant of Integration (C)
💡Reciprocals
💡Logistic Growth Equation
Highlights
The video introduces the logistic differential equation, a model for population growth.
The logistic equation includes a carrying capacity factor, representing the maximum population size an environment can support.
The rate of population change is proportional to both the population and the difference between the carrying capacity and the population.
The video demonstrates solving the logistic differential equation by separating variables.
Integration of both sides of the equation is required, which involves partial fraction decomposition for complex fractions.
The use of the cover-up method is shown to find constants in partial fraction decomposition.
The integral of the logistic equation leads to a natural logarithm involving the absolute value of the population variables.
Derivatives are taken to simplify the equation, eventually leading to the logistic growth equation form.
The final form of the logistic growth equation is presented as P(t) = M / (1 + C e^(-KT))
The constant C is determined from the initial population, and its calculation method is explained.
The video concludes with the practical application of the logistic growth model for predicting population dynamics.
An example is given to show how to use the logistic growth equation with an initial population value.
The importance of understanding the logistic equation for environmental science and biology is emphasized.
The video provides a step-by-step guide, making the complex process of solving differential equations accessible.
The presenter uses clear visual aids to illustrate the process of solving the logistic differential equation.
The video concludes with an encouragement to subscribe for more educational content on differential equations.
Transcripts
Browse More Related Video
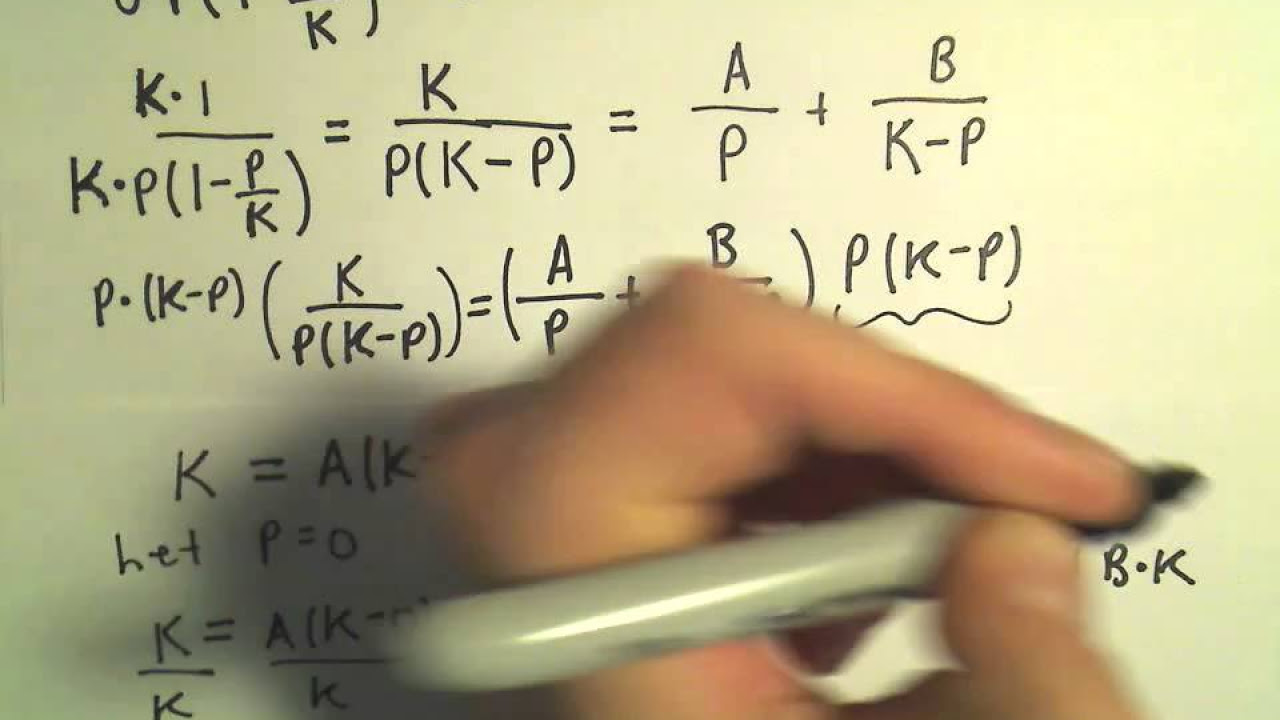
The Logistic Equation and the Analytic Solution
Logistic Growth (Separable Differential Equations)

Worked example: Logistic model word problem | Differential equations | AP Calculus BC | Khan Academy

AP Calc BC: How to Solve a Logistic Growth Application Problem
Calculus BC – 7.9 Logistic Models with Differential Equations

Solving the logistic differential equation part 2 | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: