Calculus AB/BC – 7.2 Verifying Solutions for Differential Equations
TLDRIn this calculus lesson, Mr. Bean guides students through the process of verifying solutions to differential equations. The video begins with a review of particular solutions, emphasizing the difference between general and particular solutions. Mr. Bean then demonstrates the solution to a differential equation involving an integral, using substitution and integration techniques to find the particular solution. The lesson continues with a second example, highlighting the importance of recognizing different ways a problem can be presented. A more complex problem involving the second derivative is tackled, showcasing the application of u-substitution and integration to find the solution. Mr. Bean also addresses common confusion between derivatives and antiderivatives of sine and cosine functions. The final example focuses on solving for an unknown constant in a given differential equation, illustrating the steps to find the value of the constant. The video concludes with a reminder of the importance of understanding the relationship between derivatives and antiderivatives of trigonometric functions and encourages students to apply their knowledge in solving problems.
Takeaways
- 📚 A particular solution to a differential equation is an exact solution that specifies the value of the constant term (C), as opposed to a general solution which leaves it as an unspecified constant.
- 🔍 To find a particular solution, you substitute known values into the general solution to solve for the constant term, often using a given coordinate point.
- ✏️ The process of verifying a solution involves taking derivatives of the proposed solution and ensuring it satisfies the original differential equation.
- 🧮 U-substitution is a technique used to solve integrals, particularly useful when the integrand includes a function and its derivative, which is evident in the script when solving differential equations.
- 📈 When dealing with differential equations, it's important to recognize that problems can be presented in various forms, but they often require similar methods for solving.
- 🤔 For second-derivative problems, you need to integrate twice to find the original function, being mindful of the constants of integration that arise from each integration step.
- 📉 The script emphasizes the importance of understanding the relationship between derivatives and antiderivatives, especially when dealing with trigonometric functions like sine and cosine.
- 🔢 It's crucial to keep track of constants and coefficients when manipulating algebraic expressions, as this can affect the outcome of solving for variables like 'k' in the given examples.
- 🚫 Common mistakes to avoid include confusing the signs when switching between derivatives and antiderivatives of trigonometric functions.
- 🔗 The process of solving differential equations often involves applying algebraic techniques to isolate and solve for constants or unknowns within the equation.
- 📐 The script provides a detailed walkthrough of solving differential equations, emphasizing the need for careful attention to the steps and methods used.
Q & A
What is the main topic of the lesson?
-The main topic of the lesson is to verify solutions of differential equations.
What is the difference between a particular solution and a general solution in the context of differential equations?
-A particular solution is an exact solution where the constant of integration (plus c) is determined, whereas a general solution includes the constant of integration without specifying its value.
What is the purpose of using an integral in solving differential equations?
-An integral is used to find the antiderivative of the given function, which helps in determining the particular solution to the differential equation.
How does the process of u-substitution help in solving differential equations?
-U-substitution is a technique used to simplify the integral in a differential equation, making it easier to find the antiderivative and thus the solution.
What is the role of the coordinate point in determining a particular solution?
-The coordinate point provides specific values for the variables, which are then used to solve for the constant of integration, leading to a particular solution.
How can one verify that a given function is a solution to a differential equation?
-Verification is done by taking the derivative of the proposed solution and checking if it satisfies the original differential equation.
What is the significance of recognizing different ways to write a differential equation in the context of problem-solving?
-Recognizing different forms of a differential equation allows for flexibility in problem-solving and understanding the various ways a problem can be presented, which is crucial for exams like the AP exam.
Why is it important to differentiate between the derivatives and antiderivatives of sine and cosine functions?
-Differentiating between the derivatives and antiderivatives of sine and cosine is crucial for correctly solving differential equations and avoiding confusion between the two functions.
What is the process for solving a differential equation when an unknown constant is involved?
-The process involves plugging in the given function and its derivatives into the differential equation, then solving for the unknown constant algebraically.
How does the concept of a second derivative come into play when solving differential equations?
-The second derivative is used when the differential equation involves the second order of differentiation. It requires taking the derivative twice and applying integration accordingly to find the solution.
What is the final step in solving a differential equation after finding the particular solution?
-The final step is to verify the particular solution by taking its derivative and ensuring it matches the original differential equation.
Outlines
📚 Introduction to Verifying Solutions of Differential Equations
This paragraph introduces the topic of the video, which is about verifying solutions to differential equations. Mr. Bean explains that the lesson will be a review of concepts from Unit Six, focusing on the difference between a general solution (which includes a 'plus c' after taking the anti-derivative) and a particular solution (where the constant 'c' is determined). An example is given to illustrate the process of finding a particular solution by using an integral and applying a substitution method to solve it. The paragraph ends with a verification of the solution by taking its derivative and matching it to the original differential equation.
🔍 Practice with Differential Equations and U-Substitution
The second paragraph delves into practice problems involving differential equations. It emphasizes the importance of recognizing different ways that problems can be worded while still being fundamentally the same. The paragraph continues with a complex example that involves finding the second derivative and using u-substitution to solve it. The process is intricate and requires careful application of integration techniques and algebraic manipulation. The solution is verified by showing that its derivatives match the given differential equation.
🧮 Mastering Differential Equations with Unknown Constants
The final paragraph discusses a common problem type found on AP exams where an unknown constant 'k' is involved in the function and differential equation. The task is to determine the value of 'k' using the given differential equation. The example provided involves a function with an exponential component and a sine function. By taking the first and second derivatives, applying algebraic techniques, and solving for 'k', the paragraph demonstrates how to handle such problems. It concludes with a reminder of the importance of understanding the derivatives and antiderivatives of trigonometric functions and the significance of sign changes when dealing with these functions.
Mindmap
Keywords
💡Differential Equations
💡Particular Solution
💡General Solution
💡Anti-Derivative
💡U-Substitution
💡Derivative
💡Chain Rule
💡Integration
💡Constants
💡Slope of a Curve
💡Second Derivative
Highlights
Introduction to verifying solutions of differential equations, which involves using differential equations in novel ways.
Review of a particular solution versus a general solution in the context of differential equations.
Explanation of the process to find a particular solution by determining the constant 'c' in the solution.
Use of u-substitution in integration to solve differential equations, demonstrated through an example.
Integration techniques applied to an equation involving e^(2x) - 2x^2 with respect to x.
Substitution of u=2x to simplify the integral and solve for the particular solution.
Verification of a solution by taking its derivative and ensuring it satisfies the original differential equation.
Illustration of how different problems can be phrased similarly when it comes to differential equations.
Handling of second derivative problems by integrating twice to find the original function.
Use of u-substitution for the second derivative, with careful attention to the chain rule and signs.
Solution of a complex integral involving natural logarithms, polynomials, and exponential functions.
Clarification on the common confusion between derivatives and antiderivatives of sine and cosine functions.
Technique to find an unknown constant 'k' in a given differential equation by substitution and simplification.
Use of algebraic manipulation to solve for 'k' in a second-order differential equation.
Emphasis on the importance of understanding the direction of the derivative (positive or negative) when dealing with trigonometric functions.
Final solution verification by differentiating the proposed solution and checking it against the original differential equation.
Encouragement for students to practice and master the techniques taught for solving differential equations.
Transcripts
Browse More Related Video

Calculus AB/BC – 7.7 Particular Solutions using Initial Conditions and Separation of Variables
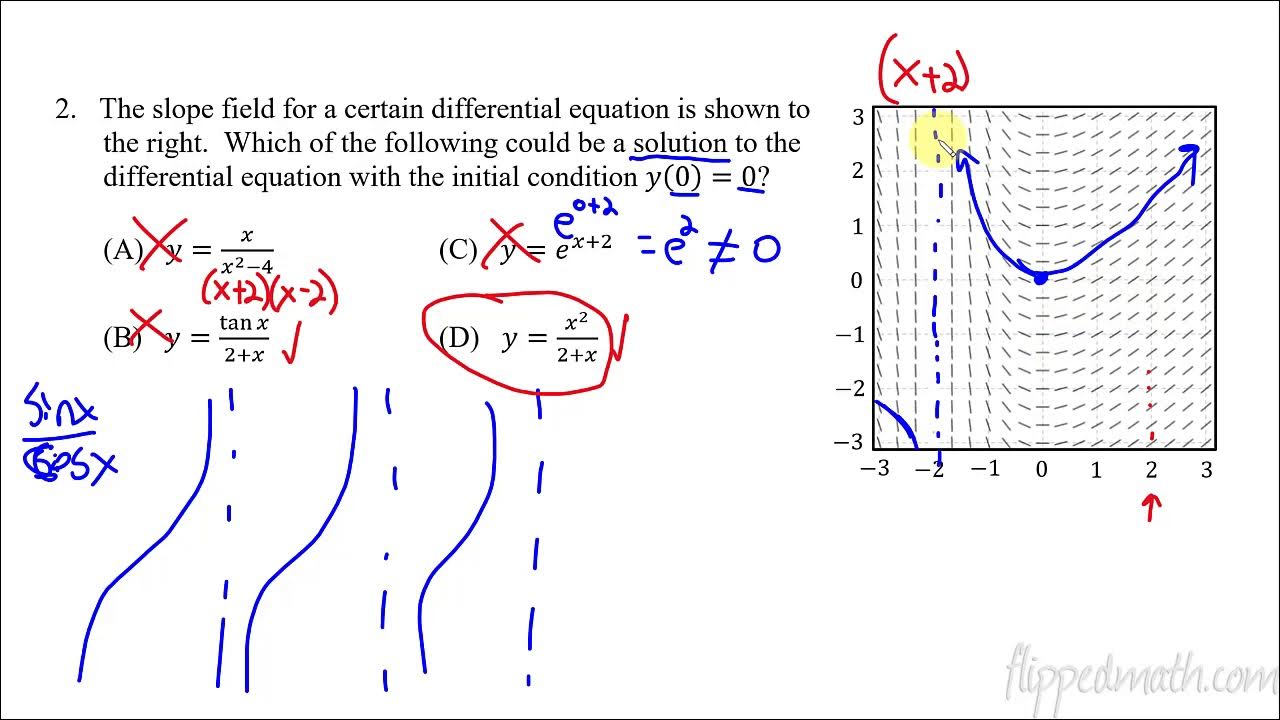
Calculus AB/BC – 7.4 Reasoning Using Slope Fields
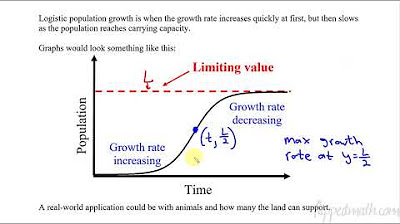
Calculus BC – 7.9 Logistic Models with Differential Equations

2022 AP Calculus AB Free Response #5

Calculus BC – 7.5 Approximating Solutions Using Euler’s Method

Introduction to Initial Value Problems (Differential Equations 4)
5.0 / 5 (0 votes)
Thanks for rating: