Calculus BC – 7.5 Approximating Solutions Using Euler’s Method
TLDRIn this engaging calculus lesson, Mr. Bean introduces students to Euler's Method, a technique used to approximate solutions to differential equations. The video is tailored for BC calculus students, as AB students do not need to be concerned with this method for their AP exam. Starting with a basic differential equation dy/dx = 1 + y, passing through the point (0,0), the instructor demonstrates how to construct tangent lines to approximate the solution curve. The step size, or delta x, is crucial and in this case is set to 0.5. By iteratively applying Euler's method, the video shows how to find successive approximations of the solution. The process involves calculating the slope at a given point, using the derivative, and then determining the new y-value by adding the product of the slope and the step size to the old y-value. The instructor emphasizes the importance of not rounding early to avoid cumulative rounding errors. The lesson concludes with a practice problem, guiding students through approximating the value of f(2) given the differential equation dy/dx = 2x, starting at the point (1,3), and using a step size of 0.2. The method is illustrated through a series of steps, ultimately leading to an approximate value for f(2). The video is both informative and practical, offering students a clear understanding of how Euler's method can be applied to find approximate solutions in calculus.
Takeaways
- 📚 Euler's Method is a technique used to find approximate solutions to differential equations.
- 🚫 AB calculus students do not need to know Euler's Method for their AP exam, it's specific to BC calculus.
- 🇨🇭 Euler, a Swiss mathematician, is the namesake of the method and is pronounced with a German accent, although many in the U.S. pronounce it differently.
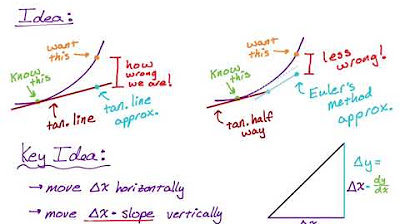
- 🔍 The method involves creating a series of tangent lines to approximate the solution curve of a differential equation.
- ➗ Delta x, or the step size, is a key component in Euler's Method and determines the accuracy of the approximation.
- 📈 The slope of the tangent line at any point is found using the derivative of the function at that point.
- 📉 As the step size decreases, the approximation using tangent lines becomes more accurate, reflecting the actual curve more closely.
- 📝 The formula for calculating the new y-value in Euler's Method is the old y-value plus the derivative times the step size (y_new = y_old + dy/dx * Δx).
- 📊 Euler's Method can be visualized by constructing a chart that organizes the information and steps taken during the process.
- 🔢 It's important to carry all decimal points as far as possible to avoid rounding errors, which can accumulate and affect the final approximation.
- 📐 The process involves repeated application of the point-slope form of a line to find new points on the curve approximation.
- 📝 Memorizing the formula and process is crucial for applying Euler's Method effectively in solving differential equations.
Q & A
Who is the main character and what subject is he teaching in this transcript?
-The main character in the transcript is Mr. Bean, and he is teaching a lesson in calculus.
What is Euler's method used for in the context of calculus?
-Euler's method is used to find an approximate solution to a differential equation.
What is the specific pronunciation of Euler that Mr. Bean suggests in the transcript?
-Mr. Bean suggests pronouncing Euler with a German pronunciation, which sounds like 'oiler'.
What is the step size (delta x) used in the example of Euler's method in the transcript?
-The step size (delta x) used in the example is 0.5.
What is the differential equation used in the example to demonstrate Euler's method?
-The differential equation used in the example is dy/dx = 1 + y.
How does the accuracy of Euler's method improve with the step size?
-The accuracy of Euler's method improves as the step size decreases, making the tangent lines more reflective of the actual curve.
What is the formula used to calculate the new y value in Euler's method?
-The formula used to calculate the new y value is y_new = y_old + (dy/dx * delta x).
What is the point that the differential equation in the example is known to go through?
-The differential equation is known to go through the point (0, 0).
What is the purpose of constructing tangent lines in Euler's method?
-Constructing tangent lines in Euler's method helps to approximate the solution curve of a differential equation by creating a series of straight lines that approximate the curve's behavior.
What is the significance of the point (1, 3) in the AP exam question mentioned in the transcript?
-The point (1, 3) is significant because it is the given initial condition for the differential equation dy/dx = 2x, and the problem asks for an approximation of the function value at x = 2 using Euler's method.
How many steps does Mr. Bean demonstrate in the AP exam question example using Euler's method?
-Mr. Bean demonstrates five steps in the AP exam question example using Euler's method.
What is the final approximation of f(2) using Euler's method in the AP exam question example?
-The final approximation of f(2) using Euler's method in the example is approximately 5.8.
Outlines
🎓 Introduction to Euler's Method in Calculus
This paragraph introduces the topic of Euler's method in calculus, specifically for BC calculus students. It clarifies that AB students do not need to learn Euler's method for their AP exam. The paragraph also discusses the general idea of finding an approximate solution to a differential equation using Euler's method, which involves constructing tangent lines at various points on the curve. The method is named after the Swiss mathematician Leonhard Euler, and the pronunciation of his name is briefly touched upon. The example used in the explanation starts with the differential equation dy/dx = 1 + y, passing through the point (0,0), and using a step size of 0.5 to construct an approximation of the solution curve.
📐 Applying Euler's Method - Step by Step
The second paragraph delves into the application of Euler's method by outlining the process of constructing tangent lines to approximate the solution curve of a differential equation. It provides a step-by-step guide on how to calculate the slope and use the point-slope form to create these lines. The paragraph also demonstrates how the step size affects the accuracy of the approximation, noting that a smaller step size results in a more accurate representation. The process is shown through an example where the differential equation is dy/dx = 1 + y, and the approximation starts from the point (0,0) with a step size of 0.5, eventually reaching a new point (1.5, 2.375) after several iterations.
🔢 Euler's Method Formula and Calculation
This paragraph focuses on the formula used in Euler's method for finding the new y value, which is the old y value plus the derivative times the step size (delta x). It emphasizes the importance of not rounding early to avoid cumulative rounding errors. The paragraph provides a worked example using the differential equation dy/dx = 2x, starting from the point (1,3) and aiming to approximate the value of f(2). The step size is calculated to be 0.2, and the process is repeated five times to reach an approximation of f(2). The paragraph concludes with an encouragement to practice the method and a reminder of the importance of accuracy in calculations.
📝 Euler's Method Summary and Practice
The final paragraph summarizes the process of Euler's method and encourages viewers to practice it to become more comfortable with the technique. It mentions that while the example shown involves five steps, typically students won't need to perform that many steps in an exam setting. The paragraph ends with an invitation to complete a mastery check and a promise to continue the lesson in the next video. The approximate value of f(2) using Euler's method is confirmed to be around 5.8, providing a clear answer to the question posed in the video.
Mindmap
Keywords
💡Calculus
💡Euler's Method
💡Differential Equation
💡Slope Field
💡Tangent Line
💡Step Size
💡Derivative
💡Point-Slope Form
💡Approximation
💡Accuracy
💡AP Exam
Highlights
Introduction to Euler's method for finding approximate solutions to differential equations.
Euler's method is not required for AB calculus students but is essential for BC calculus.
Different pronunciations of 'Euler' are acknowledged, with a nod to Swiss and German pronunciations.
The concept of 'delta x' as a step size in the context of Euler's method is explained.
Construction of tangent lines to approximate the solution curve of a differential equation.
Use of point-slope form to create tangent lines for Euler's method approximation.
The impact of step size on the accuracy of the approximation; smaller steps lead to more precise results.
Demonstration of how to calculate the slope for a tangent line using the derivative provided.
Graphical representation of how Euler's method can be visualized with tangent lines approximating a curve.
The formula for updating the y-value in Euler's method: y_new = y_old + (dy/dx * Δx).
An example problem is solved using Euler's method to approximate the value of a function at a given point.
The importance of not rounding early to avoid cumulative rounding errors in calculations.
A step-by-step guide through multiple iterations of Euler's method to reach an approximation.
The final approximation of f(2) using Euler's method is demonstrated to be approximately 5.8.
Emphasis on the practical application of Euler's method for students preparing for AP exams.
The process is summarized to highlight the key steps and formulae for Euler's method.
Encouragement for students to practice and become comfortable with the method for better understanding and accuracy.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: