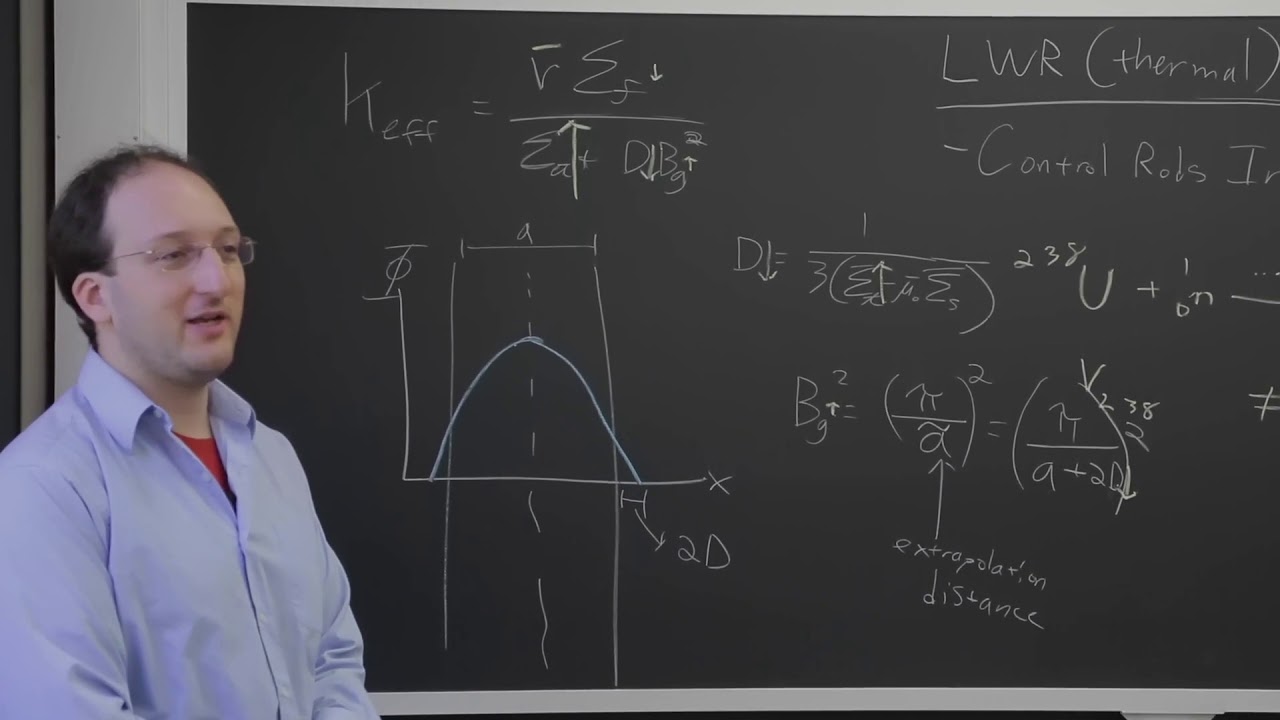23. Solving the Neutron Diffusion Equation, and Criticality Relations
TLDRThe transcript is from a lecture on nuclear reactor physics, focusing on the derivation and application of the criticality condition for a nuclear reactor. The professor begins by simplifying the neutron transport equation, excluding certain reactions and focusing on the Laplacian operator across different coordinate systems. The class then delves into solving the equation for an infinite slab reactor and a cylindrical reactor, emphasizing the importance of material properties and geometry in determining reactor criticality. The lecture progresses to explore how changes in reactor conditions, such as temperature or size, affect the effective multiplication factor (k-effective) and reactor behavior. The criticality condition is derived for a two-group energy model, which is applicable to reactors of any geometry. The professor concludes by discussing the importance of understanding how various factors can push a reactor out of equilibrium and the engineering aspects of designing a critical reactor. The lecture is rich in mathematical derivations and seeks to provide students with a solid foundation in reactor physics, preparing them for more advanced topics in subsequent classes.
Takeaways
- 📚 The content provided is under a Creative Commons license, supporting MIT OpenCourseWare in offering free educational resources.
- 🧮 The lecture covers a range of reactor problems from simple one-group homogeneous reactors to more complex two-group reactors like the AP 1000.
- 🔍 The course aims to solve the largest equation used at MIT for reactor problems and then simplify it for manageable use.
- 📉 The process involves simplifying the neutron transport equation by neglecting certain terms like NIN reactions and photo fission for ease of solving.
- 🧬 The Laplacian operator, crucial in the neutron transport equation, varies in form across different dimensions and coordinate systems.
- 📉 For an infinite slab reactor, the flux is assumed to take a cosine form due to symmetry, leading to a simplified equation for criticality.
- 🌡️ Raising the temperature in a reactor can lead to various outcomes for k-effective, depending on the materials used, which is important for reactor feedback.
- ⚖️ The criticality condition (k-effective) is determined by the ratio of gains (from fission) to losses (from absorption and leakage) of neutrons.
- 🚦 Controlling a reactor's power is complex due to time-dependent effects and delayed neutrons, which can affect reactivity.
- 🔢 The power of a reactor and its criticality are not directly linked, as a reactor can be critical with varying power outputs.
- 🤔 The two-group model separates neutrons into fast and thermal energy groups, allowing for a more detailed analysis of reactor behavior.
- 🔧 The final criticality condition for a two-group reactor is expressed in terms of material properties and geometry, providing a tool for reactor design.
Q & A
What is the purpose of MIT OpenCourseWare?
-MIT OpenCourseWare aims to provide high-quality educational resources for free, and it relies on donations to continue offering these materials.
What is the largest equation discussed in the context of the MIT course?
-The largest equation discussed is related to reactor problems, involving neutron transport and reactor physics.
What are the different types of reactors mentioned in the script?
-The script mentions simple one-group homogeneous reactors and two-group reactors, like the AP 1000 reactor, which separates neutrons into fast and thermal groups.
What is the significance of the Laplacian operator in the context of reactor physics?
-The Laplacian operator is used to describe the flux of neutrons in different dimensions and coordinate systems, which is crucial for solving reactor problems.
What is the extrapolation length in the context of reactor physics?
-The extrapolation length is a distance equal to two times the diffusion constant, which represents how far neutrons can travel before they are effectively lost from the reactor.
How is the criticality condition derived in the script?
-The criticality condition is derived by simplifying the neutron diffusion equation, canceling out terms, and focusing on the ratio of gains to losses of neutrons in the reactor.
What is the relationship between the reactor's temperature and its effective multiplication factor (k-effective)?
-Raising the temperature can lead to a decrease in cross-sections, which may affect k-effective in complex ways depending on the materials used in the reactor. It can either lead to a sub-critical state or, if designed poorly, could increase k-effective, which is undesirable.
How does the size of the reactor affect its criticality?
-Making the reactor larger, without changing the materials, generally increases k-effective, assuming the geometry and material properties remain constant.
What is the role of the neutron multiplication factor (nu) in the criticality condition?
-The neutron multiplication factor (nu) represents the average number of neutrons produced by fission per fission event and is a key component in the criticality condition, representing the gain mechanism in the reactor.
Why are Bessel functions relevant to solving reactor problems in cylindrical geometry?
-Bessel functions are solutions to the Laplacian equation in cylindrical coordinates, making them useful for describing the flux distribution in cylindrical reactors.
What is the importance of understanding the criticality condition in reactor design?
-Understanding the criticality condition is essential for designing a reactor that operates at a perfect balance, ensuring it is critical (k-effective equals 1), and for predicting how changes in the reactor's conditions or materials will affect its criticality.
Outlines
📚 Introduction to Reactor Problems and Equations
The paragraph introduces the concept of solving reactor problems using the neutron transport equation. It discusses the process of simplifying the equation to a manageable size and applying it to various reactor scenarios, such as one-group and two-group reactors. The professor emphasizes the importance of understanding how to use the equation to analyze different reactor configurations and their neutron flux patterns.
🧠 Solving Differential Equations and Flux Forms
This section delves into the methodology of solving differential equations by simplifying and guessing solutions based on previous knowledge. The professor explains how to derive the form of the flux solution, which takes into account the Laplacian operator and its different forms in various coordinate systems. The discussion highlights the use of symmetry in solving for the flux profile and introduces the concept of the extrapolation length in the context of reactor shielding.
🔧 Criticality Condition and Reactor Balance
The paragraph focuses on establishing the criticality condition for a reactor by examining the balance between neutron gains and losses. It explains how changes in material properties, such as cross-sections and the diffusion constant, affect the criticality (k-effective) of the reactor. The professor also introduces the concept of reactor feedback, discussing how temperature changes can influence reactor behavior and the importance of designing reactors with negative temperature coefficients.
💡 Power Generation and Reactor Dynamics
This part of the script discusses the source of power in a reactor, which comes from the kinetic energy of neutrons, and how it is separate from the criticality of the reactor. The professor addresses the relationship between reactor power and criticality, emphasizing that a reactor can be critical at various power levels. The discussion also touches on the dynamics of controlling a reactor, including the effects of withdrawing control rods and the time-dependent nature of reactor behavior.
🌐 Two-Group Balance Equations and Neutron Interactions
The paragraph introduces the two-group balance equations, which separate neutrons into fast and thermal energy groups. The professor explains the gains and losses of neutrons in each group, considering factors such as fission, absorption, and scattering. The section also addresses the concept of the birth spectrum and how it would affect the criticality condition if some neutrons were born in the thermal group.
📈 Solving the Two-Group Criticality Condition
This section presents the process of solving for the criticality condition in a two-energy group reactor. The professor demonstrates how to derive an expression for k-effective in terms of material properties and geometry. The discussion includes the concept of geometric buckling and how it relates to the reactor's design. The professor emphasizes the importance of understanding the ratio of gains to losses in maintaining reactor equilibrium.
🤔 Application of the Criticality Condition and Reactor Design
The paragraph discusses the practical application of the criticality condition in designing a reactor. It highlights the importance of selecting appropriate materials and understanding their properties to ensure the reactor is critical. The professor also touches on the implications of different physical changes to the reactor, such as altering the geometry or material composition, and how these changes would affect the reactor's criticality.
Mindmap
Keywords
💡Neutron Transport Equation
💡Criticality Condition
💡Flux
💡Laplacian Operator
💡Diffusion Constant
💡Effective Multiplication Factor (k-effective)
💡Two-Group Reactor Model
💡Cross-Sections
💡Steady State
💡Temperature Feedback
💡Bessel Functions
Highlights
The lecture introduces the largest equation likely to be used at MIT, focusing on reactor problems from simple one-group homogeneous reactors to more complex two-group reactors.
The equation is simplified by neglecting NIN reactions and photo fission, leading to a more manageable form.
The Laplacian operator is discussed in different dimensions and coordinate systems, with a focus on 1D Cartesian and cylindrical cases.
An infinite slab reactor is used as an example for easier analytical solution, before moving on to more complex cylindrical reactors.
The form of the flux function is derived, assuming it takes the shape of a cosine function, influenced by symmetry considerations.
The concept of the extrapolation length is introduced, which is crucial for shielding and neutron streaming out of the reactor.
The diffusion constant is expressed in terms of cross sections and material properties, providing a physical analogy for the reactor's behavior.
The criticality condition is derived, showing that the reactor's k-effective is a ratio of gains to losses of neutrons.
The impact of increasing reactor absorption on k-effective is explored, leading to a sub-critical state.
The effects of raising the reactor's temperature on cross sections and k-effective are discussed, including the concept of Doppler broadening.
The concept of reactor feedback is introduced, explaining how changes in temperature or geometry can affect k-effective.
The relationship between reactor power and criticality is clarified, noting that they are not necessarily linked.
The steady state of a reactor is discussed, including the effects of withdrawing or inserting control rods.
The two-group balance equations are introduced for a more detailed analysis of reactors, separating neutrons into fast and thermal groups.
The gains and losses for both fast and thermal neutron groups are quantified, leading to a criticality condition for a two-energy group reactor.
The importance of the geometric buckling term, bg squared, is emphasized for defining reactor geometry in the criticality condition.
The final criticality condition for a two-group reactor is derived, showing it as a ratio of material properties and geometry.
The lecture concludes with an invitation for students to ask questions about the material and its applications.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: