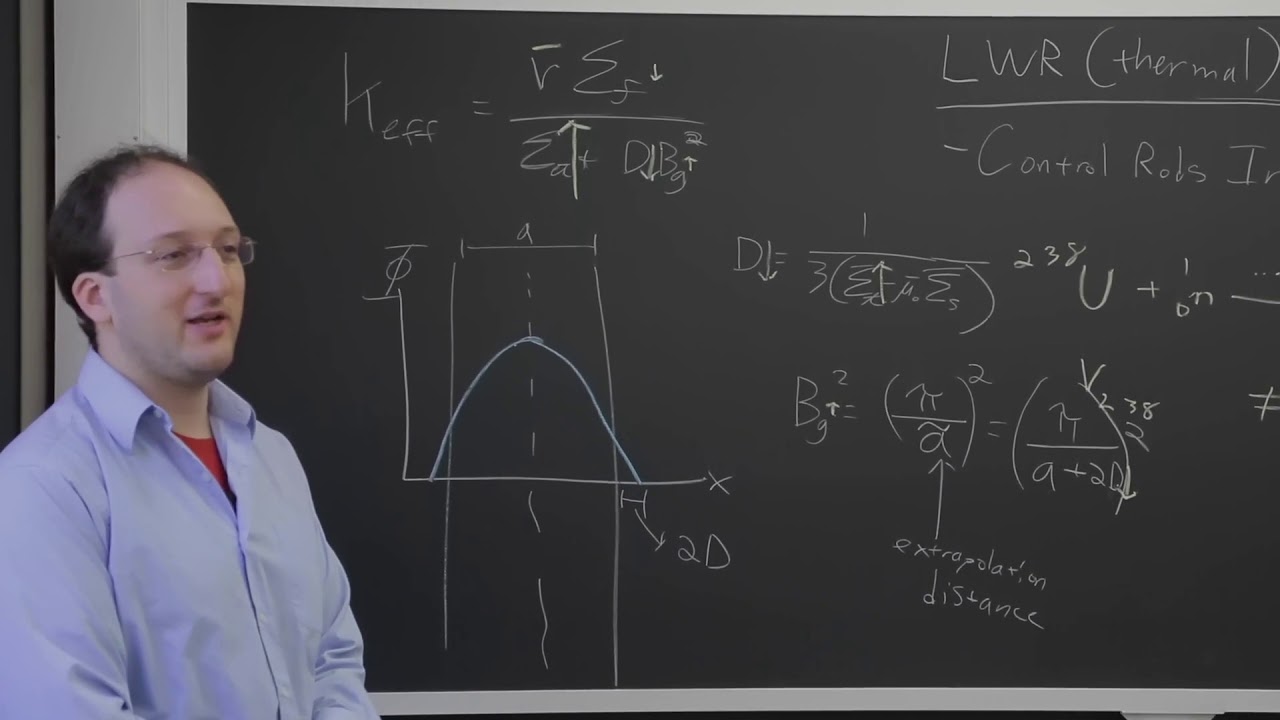22. Simplifying Neutron Transport to Neutron Diffusion
TLDRThe provided script is a detailed lecture on neutron diffusion and reactor criticality within the context of nuclear engineering. The lecturer, Michael Short, simplifies complex concepts by starting with a comprehensive neutron balance equation and systematically reducing it through various assumptions—such as steady state, homogeneity, and neglecting certain variables like angle and time—to arrive at a more manageable form. The lecture covers essential topics like fission, absorption, leakage, and the role of control rods and fuel in a reactor's operation. It also touches on the use of Fick's law to approximate neutron behavior as a diffusing substance. The criticality condition is derived, explaining the terms subcritical, critical, and supercritical in the context of reactor operation. The lecture concludes with a discussion on the practical application of these concepts in real-world reactors, emphasizing the importance of a balanced reactor and the common misconceptions about the term 'critical' in nuclear engineering.
Takeaways
- 📚 The lecture is about simplifying the neutron diffusion equation to understand criticality in a nuclear reactor.
- 🌈 The process involves a 'rainbow explosion' of simplifications, neglecting variables like angle, time, and assuming homogeneity and steady state conditions.
- 🎓 The lecturer emphasizes that even though simplifications are made for educational purposes, they reflect actual practices in nuclear reactor design.
- ⏱️ The time-dependent term is initially included but later removed under the assumption of a steady-state reactor condition.
- 🚫 The external source term is eliminated on the assumption that the reactor is self-sustaining once at steady state.
- 🔄 The homogeneity assumption allows for neglecting spatial dependence of cross-sections, which simplifies the equation significantly.
- 🤔 The assumption of homogeneity breaks down near control rods and fuel where material properties change abruptly.
- 🧮 The energy dependence of cross-sections is averaged over the energy range, which simplifies the equation further.
- 📉 The leakage term is accounted for with a negative sign because it represents neutrons leaving the system, despite the positive diffusion term.
- 🤓 The final form of the neutron diffusion equation is a second-order linear differential equation that can be solved for flux.
- 🔑 The criticality condition (k-effective) is derived from the balance of gains and losses, where k-effective equals 1 for a critical reactor.
Q & A
What is the main purpose of MIT OpenCourseWare?
-The main purpose of MIT OpenCourseWare is to offer high-quality educational resources for free, allowing anyone to access the materials from hundreds of MIT courses.
What is the focus of the lecture on the day described in the transcript?
-The focus of the lecture is on simplifying the neutron diffusion equation to understand criticality in a reactor, by canceling out terms to reach a homogeneous infinite reactor criticality condition.
What are the units of neutron flux?
-The units of neutron flux are neutrons per centimeter squared per second (n/cm²/s).
Why is the term 'critical' in nuclear terminology not as scary as it sounds to the general public?
-In nuclear terminology, 'critical' means the reactor is in perfect control or balance, which is a desired state. It does not imply a loss of control or danger, despite the emotional connotations the word may evoke in a non-technical context.
What is the significance of the variable 'k effective' in the context of reactor physics?
-The variable 'k effective' (keff) signifies the ratio of neutrons produced to neutrons consumed in a reactor. If keff equals 1, the reactor is critical, meaning it is in a state of equilibrium where the number of neutrons produced equals the number consumed.
What is the one-group approximation in reactor physics?
-The one-group approximation is a simplification in reactor physics where all energy groups of neutrons are combined into a single group, disregarding the energy dependence of neutron interactions within the reactor.
How does the neutron diffusion equation relate to the criticality condition of a reactor?
-The neutron diffusion equation describes the flow of neutrons in a reactor, taking into account factors like fission, absorption, leakage, and scattering. The criticality condition is derived from this equation, defining the state where the reactor neither gains nor loses neutrons on average, which is when keff equals 1.
What is the role of the fission birth spectrum (chi) in the neutron diffusion equation?
-The fission birth spectrum (chi) represents the distribution of neutrons released during fission over all possible directions. In the one-group approximation, it simplifies to a value of 1, as it is assumed that all neutrons are born within the single energy group considered.
What is the leakage term in the neutron diffusion equation, and why is it considered negative?
-The leakage term represents the loss of neutrons from the reactor due to their movement out of the control volume. It is considered negative because it represents a loss of neutrons, and in the context of the diffusion equation, it is defined as such to indicate a reduction in the neutron population.
Why does the lecturer suggest that the neutron transport equation simplifies to the neutron diffusion equation under certain assumptions?
-The neutron transport equation is a more complex and accurate model of neutron behavior, but it is difficult to solve analytically. By making certain approximations such as treating neutrons like a diffusing gas or chemical, the problem simplifies to the neutron diffusion equation, which is more tractable and can be solved more easily.
What is the purpose of the electron microscope session mentioned at the end of the transcript?
-The electron microscope session aims to provide hands-on experience with electron microscopy, allowing students to analyze different materials by imaging them with electrons. This session will also involve producing and analyzing X-ray spectra to understand various features such as bremsstrahlung and characteristic peaks.
Outlines
🎨 Introduction to MIT OpenCourseWare and Neutron Diffusion
The video begins with an introduction to MIT OpenCourseWare and its commitment to providing free educational resources, encouraging donations to support the initiative. The lecturer, Michael Short, expresses enthusiasm about using various colors to illustrate a complex equation. The central topic is the neutron diffusion equation in the context of a nuclear reactor, focusing on criticality conditions and the interplay between fission, absorption, and leakage of neutrons. The lecture also touches on the mathematical intensity of the previous session and the satisfaction of simplifying complex equations.
📚 Detailed Breakdown of the Neutron Diffusion Equation
This paragraph delves into the specifics of the neutron diffusion equation, discussing the various terms and their significance in the context of a nuclear reactor's operation. It covers the concepts of flux, current, and the role of cross-sections in reaction rates. The lecturer simplifies the equation by applying the divergence theorem and neglecting certain variables like angle and time under the assumption of a steady-state reactor. The process involves integrating over energy, volume, and surface, and the use of a control volume to account for neutron behavior within the reactor.
🔍 Simplify Assumptions for Reactor Design
The focus shifts to the perspective of a reactor designer, emphasizing the simplification process by neglecting variables like angle and time. The assumption of a homogeneous reactor is introduced, which allows for the elimination of spatial dependence in cross-sections. The lecturer discusses scenarios where the homogeneity assumption breaks down, such as near control rods and fuel. The video also explores the concept of a molten salt fueled reactor as an example of a homogeneous reactor system.
🧮 Simplifying the Equation Further with Energy Discretization
The paragraph discusses the challenges of analytically solving the neutron diffusion equation due to its energy-dependent terms. To address this, the video introduces methods of energy discretization, such as dividing the energy spectrum into groups. It highlights that for light water reactors, a two-group approximation is often sufficient, distinguishing between thermal and non-thermal neutrons. The process of averaging cross-sections over energy ranges is explained, which simplifies the complex equation into a more manageable form.
🚧 Transition from Neutron Transport to Diffusion Equation
The lecturer transitions from the neutron transport equation to the diffusion equation by making significant approximations. This involves treating neutrons as a diffusing substance similar to a gas or chemical, using Fick's law to describe their behavior. The current term in the equation is replaced with a diffusion term, leading to a simplified second-order linear differential equation. The video emphasizes that while this approximation works well in most of the reactor, it may not be accurate near areas with rapidly changing cross-sections, such as control rods or fuel.
🔑 Criticality Conditions and Neutron Balance
The final paragraph defines the criticality condition of a reactor, explaining the concept of k-effective, which is the ratio of neutrons produced to neutrons consumed. The video describes how a reactor is critical when k-effective equals 1, indicating a balance between neutron production and absorption. It also touches on the terms subcritical and supercritical, dispelling the notion that going critical is inherently dangerous. Instead, it signifies a controlled and balanced state. The neutron balance equation is simplified to reflect gains and losses, leading to the condition for criticality.
❓ Addressing Queries and Upcoming Practical Sessions
The video concludes with an invitation for questions from the audience, addressing topics such as energy groups and the practical application of the one-group and two-group models in reactor analysis. The lecturer also teases upcoming sessions involving the electron microscope, where students will analyze materials and produce X-ray spectra, providing a hands-on experience to complement the theoretical knowledge gained in the lecture.
Mindmap
Keywords
💡Criticality
💡Fission
💡Neutron Diffusion Equation
💡Flux
💡Cross-Section
💡Steady State
💡Leakage
💡Homogeneous Reactor
💡One-Group Approximation
💡Fick's Law
Highlights
The lecture discusses the simplification of the neutron diffusion equation for reactor criticality analysis.
The process involves canceling out terms to reach a homogeneous infinite reactor criticality condition.
Variables such as flux, current, and reaction rate are defined and used throughout the equation.
The importance of understanding the spatial and energy dependence of neutron behavior in a reactor is emphasized.
The concept of a control volume and its role in neutron balance within the reactor is explained.
External sources of neutrons, such as californium kickstarter sources, are introduced as part of the reactor's operation.
The lecture covers the treatment of different reactions like fission, nin reactions, and photofission in the neutron diffusion equation.
The scattering term and its significance in neutron energy loss and group transition are discussed.
The application of the divergence theorem to simplify the leakage term in the neutron diffusion equation is shown.
The neglect of angle dependence in the reactor's neutron balance for simplification purposes is justified.
The assumption of a steady-state reactor to eliminate transient terms from the equation is explained.
The concept of homogeneity in the reactor and its implications on the simplification of cross-sectional dependencies is discussed.
The use of energy discretization and the one-group approximation for simplifying the neutron diffusion equation is introduced.
The averaging of cross-sections over an energy range to account for different reaction rates is explained.
The application of Fick's law to the neutron current term to derive the neutron diffusion equation is covered.
The criticality condition (k-effective) and its relation to reactor stability and control is defined.
The difference between subcritical, critical, and supercritical states of a reactor is clarified.
The lecture concludes with the one-group homogeneous steady-state neutron diffusion equation, which is solvable for flux profiles.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: