Elastic Potential Energy - Introductory Example Problems
TLDRThe video script presents two examples to demonstrate the concept and equation of elastic potential energy, also known as spring potential energy. In the first example, a spring with a spring constant of 2.6 N/m is stretched 7 m, and the potential energy is calculated using the formula PE = (1/2) * k * x^2, resulting in 0.637 J. The second example involves a truck suspension spring with a spring constant of 769 N/m, where the potential energy is given as 250 J, and the problem is to find the compression distance, which is calculated to be 0.81 m. Both examples effectively illustrate the application of the elastic potential energy formula.
Takeaways
- 📚 Elastic potential energy is also known as spring potential energy, which is a key concept in physics.
- 🔢 The formula for elastic potential energy (PE) in a spring is PE = (1/2) * k * x^2, where k is the spring constant and x is the displacement from the equilibrium position.
- 🌐 In the first example, a spring with a spring constant (k) of 2.6 N/m is stretched by 0.7 m, resulting in an elastic potential energy of 0.637 J.
- 🔧 The spring constant is a measure of the 'stiffness' of the spring and is denoted by the symbol K.
- 🚚 In the second example, a truck suspension spring with a spring constant of 769 N/m has an elastic potential energy of 250 J.
- 📈 The potential energy stored in a spring is directly proportional to the square of the displacement (x) and the spring constant (k).
- 🧠 Understanding the relationship between the spring constant, displacement, and potential energy is crucial for solving related physics problems.
- 📝 When solving problems, it's important to use consistent units, such as meters for displacement and Newtons for the spring constant.
- 🔍 The process of solving these problems involves substituting the given values into the formula and performing the necessary calculations to find the unknown variable.
- 🎯 In the second example, solving for the displacement (x) involved dividing both sides of the equation by the constant term and then taking the square root of the result.
- 📊 The examples provided in the script demonstrate the practical application of the elastic potential energy concept in real-world scenarios, such as the functioning of a truck suspension system.
Q & A
What is the formula for calculating the elastic potential energy of a spring?
-The formula for calculating the elastic potential energy (PE) of a spring is PE = 1/2 * k * x^2, where 'k' is the spring constant and 'x' is the displacement of the spring from its equilibrium position.
In the example involving a spring with a spring constant of 2.6 Newtons per meter stretched by 7 meters, how is the elastic potential energy calculated?
-To calculate the elastic potential energy, substitute the values into the formula: PE = 1/2 * k * x^2. Here, k = 2.6 Newtons per meter and x = 7 meters. The calculation would involve squaring the displacement (x) and multiplying it by the spring constant (k) divided by 2.
What was the calculated elastic potential energy for the spring stretched 7 meters?
-The calculated elastic potential energy for the spring stretched 7 meters was 0.637 Joules.
How do you solve for the displacement 'x' when the potential energy and spring constant are known?
-To solve for the displacement 'x', rearrange the elastic potential energy formula to solve for 'x^2'. This involves dividing the known potential energy by 1/2 of the spring constant, and then taking the square root of the result. For example, with a PE = 250 Joules and k = 769 Newtons/meter, you find 'x' by isolating it in the equation and calculating accordingly.
What is the relationship between the spring constant and the elastic potential energy?
-The spring constant (k) is directly proportional to the elastic potential energy. A higher spring constant means that more force is needed to compress or stretch the spring, resulting in a greater amount of stored energy for a given displacement.
What was the estimated displacement for the truck suspension spring when the potential energy was given as 250 Joules?
-The estimated displacement for the truck suspension spring, when the potential energy was 250 Joules, was approximately 0.81 meters.
How does the choice of using 'd' or 'x' for displacement affect the calculation in physics problems?
-In the context of spring problems, 'x' is typically used to represent displacement because it specifically refers to the distance an object has been compressed or stretched from its natural length. Using 'd' might be confusing as it is often used more generally for distance in other physics contexts.
Why is it important not to round off values prematurely in physics calculations?
-It is important not to round off values prematurely to ensure accuracy in the final results. Early rounding can lead to significant errors in the calculation, especially in problems involving multiple steps or when small changes in values can result in large differences in outcomes.
What does the term 'elastic potential energy' specifically refer to?
-Elastic potential energy refers to the energy stored in elastic materials as a result of their stretching or compressing. This energy is recoverable and is a specific form of potential energy related to the forces between atoms and molecules in the material.
What did the problem involving the truck suspension springs demonstrate about practical applications of physics?
-The problem involving truck suspension springs demonstrated how physics and specifically the concept of elastic potential energy apply to real-world engineering challenges, such as designing vehicle suspensions that can absorb impacts effectively using springs with precise characteristics.
Outlines
📚 Elastic Potential Energy Calculation
The paragraph discusses the application of the concept and formula for elastic potential energy, also known as spring potential energy. A spring with a spring constant of 2.6 N/m is stretched by 0.7 m, and the speaker calculates the potential energy using the formula PE = (1/2) * k * x^2. By substituting the given values, the speaker finds the elastic potential energy to be 0.637 J. The speaker also addresses a second problem involving a truck suspension spring with a spring constant of 769 N/m and a potential energy of 250 J, from which they calculate the compression distance to be 0.81 m. The explanation emphasizes understanding the formula and its application to real-world problems.
🎉 Correct Application of Elastic Potential Energy
The speaker confirms the correctness of their calculations and application of the elastic potential energy concept and formula in the previous paragraph. They summarize the process of using the formula PE = (1/2) * k * x^2 to determine the potential energy in given scenarios involving springs. The speaker highlights the importance of understanding the concept and applying it accurately to solve problems related to elastic potential energy.
Mindmap
Keywords
💡Elastic Potential Energy
💡Spring Constant
💡Stretched
💡Compressed
💡Potential Energy
💡Formula
💡Deformation
💡Newtons per Meter
💡Joules
💡Truck Suspension Springs
💡Calculation
Highlights
The concept of elastic potential energy is introduced, which is also known as spring potential energy.
A spring with a spring constant of 2.6 Newtons per meter is used in the example to demonstrate the concept.
The spring is stretched by a distance of 7 meters, and the potential energy of the system is to be calculated.
The formula for elastic potential energy is given as the potential energy being equal to 1/2 of the spring constant times the distance squared.
The potential energy is calculated to be 0.637 Joules using the provided formula and values.
A truck suspension system with springs having a spring constant of 769 Newtons per meter is discussed in the second example.
The potential energy of the front right spring is given as 250 Joules.
The goal is to find out how far the spring is compressed, given the potential energy and spring constant.
The formula for elastic potential energy is used again, with the potential energy set to 250 Joules to solve for the compressed distance.
By solving the equation, the compressed distance is found to be 0.81 meters.
The process demonstrates the practical application of the elastic potential energy concept in understanding and analyzing spring systems.
The examples provided illustrate the step-by-step method for calculating potential energy in spring systems.
The importance of not rounding off intermediate results in calculations is emphasized to ensure accuracy.
The transcript serves as an educational resource for learning about elastic potential energy and its calculation.
The use of the spring constant and distance in the formula highlights the relationship between these physical quantities.
The examples show how to apply theoretical concepts to real-world problems, such as analyzing the energy in a truck's suspension system.
The transcript provides a clear and detailed explanation of the concept, making it accessible to learners.
The methodical approach to problem-solving showcased in the transcript can be applied to other physics problems as well.
The transcript emphasizes the importance of understanding the underlying concepts to correctly apply the formulas.
The practical examples given in the transcript help to bridge the gap between theoretical physics and real-world scenarios.
The transcript's detailed walkthrough of the problem-solving process can aid in the development of critical thinking and analytical skills.
Transcripts
Browse More Related Video

GCSE Physics - Elastic Potential Energy and F = ke Equations #45

(previous version) Introduction to Elastic Potential Energy with Examples

Introduction to Elastic Potential Energy with Examples

Potential energy stored in a spring | Work and energy | Physics | Khan Academy
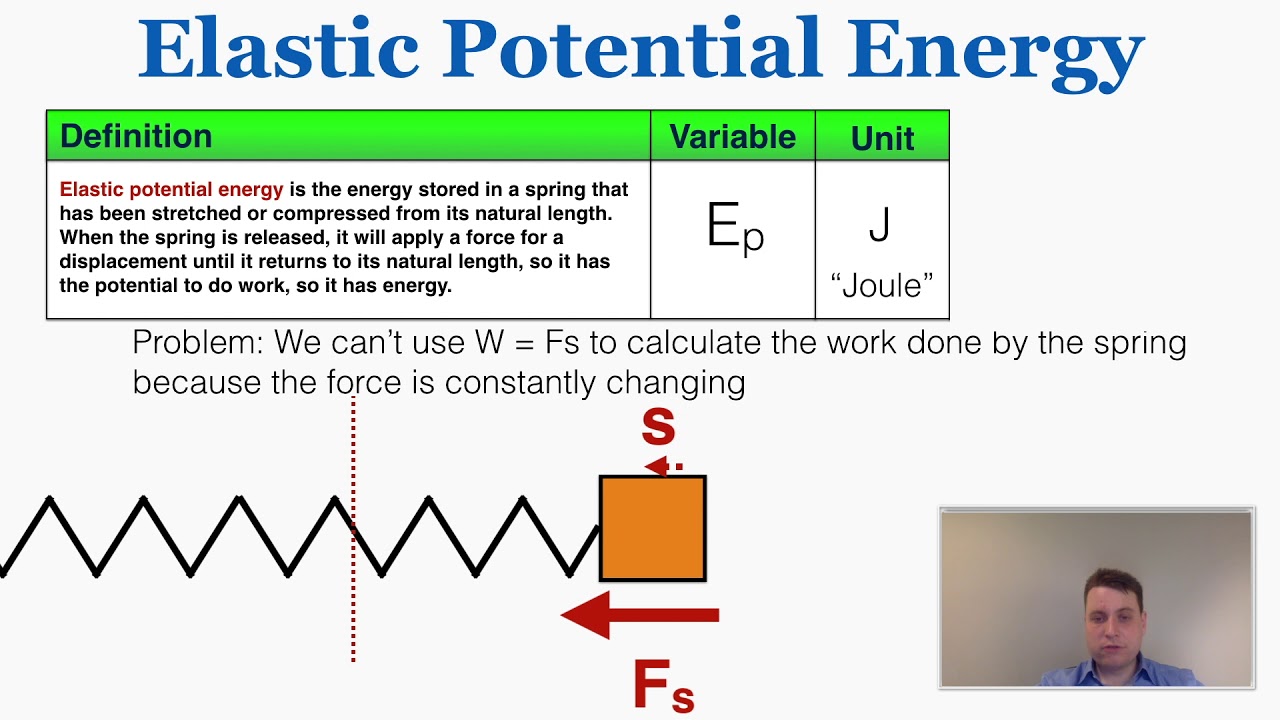
Elastic Potential Energy - IB Physics
Kinetic Energy - Introductory Example Problems
5.0 / 5 (0 votes)
Thanks for rating: