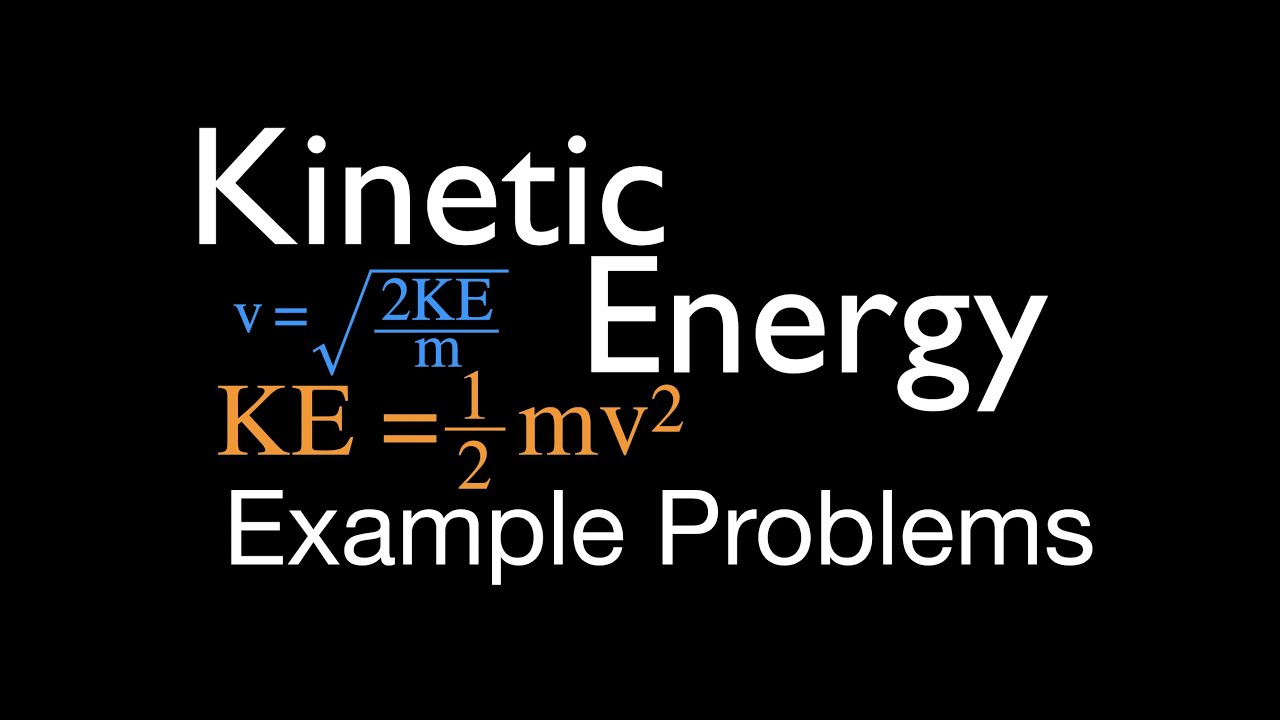Kinetic Energy - Introductory Example Problems
TLDRThis script demonstrates how to apply the kinetic energy formula to solve two physics problems. The first problem involves calculating the kinetic energy of a 15 kg cart moving at 4.2 m/s down a hill, resulting in 132.3 joules. The second problem is an inverse calculation where, given a car's mass (1600 kg) and its kinetic energy (125,000 joules), the script shows how to determine its velocity, concluding with a speed of 12.5 m/s. Both examples effectively illustrate the process of using the kinetic energy formula (1/2 * mass * velocity^2) to find unknown quantities in physics scenarios.
Takeaways
- 📚 The kinetic energy formula is crucial for solving these physics problems, expressed as KE = (1/2)mv^2 where KE is kinetic energy, m is mass, and v is velocity.
- 🛷 In problem one, a cart weighing 15 kg rolls down a hill at 4.2 m/s, and its kinetic energy is calculated using the given mass and velocity.
- 📈 The calculation for the cart's kinetic energy results in 132.3 joules, demonstrating how the formula is applied to real-world scenarios.
- 🚗 Problem two involves a car with a mass of 1600 kg and a known kinetic energy of 125,000 joules, where the task is to find the car's velocity.
- 🔢 The process of solving for velocity involves rearranging the kinetic energy formula to solve for v, and performing the necessary algebraic calculations.
- 🎯 After simplifying the equation, the velocity squared (v^2) is found to be 150, which is the next step in determining the car's speed.
- 🌟 Taking the square root of both sides of the equation yields the velocity (v = √150), which is approximately 12.25 m/s for the car in the example.
- 💡 These examples illustrate the importance of understanding and applying the kinetic energy formula to calculate the energy and velocity of moving objects.
- 📊 The script provides a clear step-by-step process for solving physics problems, emphasizing the importance of accurate calculations and unit consistency.
- 🔍 The examples also highlight the need to interpret the results correctly, such as distinguishing between velocity squared and the actual velocity.
- 🌐 The principles and methods discussed are universally applicable across various contexts within physics and engineering, showcasing the versatility of the kinetic energy formula.
Q & A
What is the formula for calculating kinetic energy?
-The formula for calculating kinetic energy is KE = (1/2) * m * v^2, where KE is the kinetic energy, m is the mass of the object, and v is its velocity.
What was the mass of the cart in the first problem?
-The mass of the cart in the first problem was 15 kilograms.
What was the velocity of the cart rolling down the hill in the first problem?
-The velocity of the cart rolling down the hill in the first problem was 4.2 meters per second.
What was the calculated kinetic energy of the cart in the first problem?
-The calculated kinetic energy of the cart in the first problem was 132.3 joules.
In the second problem, what was the mass of the car with a kinetic energy of 125,000 joules?
-In the second problem, the mass of the car was 1600 kilograms.
How was the velocity of the car determined in the second problem?
-The velocity of the car was determined by rearranging the kinetic energy formula to solve for velocity, and then plugging in the given mass and kinetic energy values.
What was the calculated velocity of the car in the second problem?
-The calculated velocity of the car in the second problem was 12.5 meters per second.
What is the significance of the kinetic energy formula in physics?
-The kinetic energy formula is significant in physics as it quantifies the energy of an object in motion, which is a fundamental concept in understanding and analyzing motion, work, and forces in various physical systems.
Why is it important to square the velocity in the kinetic energy formula?
-The velocity is squared in the kinetic energy formula because the energy an object possesses due to its motion increases with the square of its velocity. This means that even a small increase in velocity can result in a significant increase in kinetic energy.
How does the mass of an object affect its kinetic energy?
-The mass of an object has a direct impact on its kinetic energy. As the mass of an object increases, its kinetic energy also increases, given the same velocity. This is because a more massive object requires more energy to accelerate and maintain motion.
What is the unit of kinetic energy mentioned in the script?
-The unit of kinetic energy mentioned in the script is joules.
What mathematical operation is used to isolate the velocity variable in the kinetic energy formula?
-To isolate the velocity variable in the kinetic energy formula, division and square root operations are used. First, the equation is divided by the mass constant (800 in the example), and then the square root is taken to solve for velocity.
Outlines
🚀 Solving Kinetic Energy Problems
This paragraph introduces the process of solving two distinct problems using the kinetic energy formula. The first problem involves calculating the kinetic energy of a 15 kg cart moving at 4.2 m/s down a hill, resulting in 132.3 joules of kinetic energy. The second problem is a reverse calculation where, given a car's mass (1600 kg) and its kinetic energy (125,000 joules), the task is to find its velocity. By applying the kinetic energy formula (1/2 * mass * velocity^2), the velocity is determined to be 12.5 m/s. The explanation emphasizes the importance of understanding the formula and the steps to perform the calculations, showcasing two examples of how to apply the kinetic energy concept in problem-solving.
Mindmap
Keywords
💡Kinetic Energy
💡Mass
💡Velocity
💡Formula
💡Calculation
💡Cart
💡Car
💡Joules
💡Squaring
💡Square Root
💡Physics
Highlights
The kinetic energy formula is derived and applied to solve two problems involving a cart and a car.
The mass of the cart is given as 15 kilograms, and its velocity is 4.2 meters per second.
The formula for kinetic energy is KE = 1/2 * mass * velocity^2.
Substituting the given values, the kinetic energy of the cart is calculated to be 132.3 joules.
In the second problem, the mass of the car is 1600 kilograms and its kinetic energy is 125,000 joules.
The formula for kinetic energy is rearranged to solve for the velocity (v = sqrt(2 * KE / mass)).
The velocity of the car is found to be 12.5 meters per second by taking the square root of (2 * KE / mass).
The importance of squaring the velocity when calculating kinetic energy is emphasized.
The process of simplifying the equation by dividing by the mass before solving for velocity is explained.
The concept of kinetic energy, which is the energy of motion, is introduced.
The relationship between mass, velocity, and kinetic energy is explored through the two example problems.
The formula for kinetic energy is derived from basic principles, making it easy to understand.
The step-by-step process of solving the problems using the formula is clearly outlined.
Real-world examples of a cart and a car are used to make the concept more relatable.
The calculation of kinetic energy is demonstrated using a calculator for ease of understanding.
The concept of taking the square root to find the velocity from the kinetic energy formula is explained.
The practical applications of the kinetic energy formula in calculating the energy of moving objects are highlighted.
The video provides a comprehensive understanding of the kinetic energy formula and its applications.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: