Potential energy stored in a spring | Work and energy | Physics | Khan Academy

Khan Academy
15 Apr 200810:00
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the principles of compressing and stretching a spring, focusing on Hooke's Law and the concept of potential energy. It explains how the force required to compress a spring is directly proportional to the displacement from its natural state, forming a linear relationship. The script then delves into calculating the work done in compressing the spring, which is found to be equivalent to the potential energy stored in the spring. The work is visualized as the area under a triangular force-displacement graph, and the formula for potential energy (1/2Kx^2) is derived, where K is the spring constant and x is the displacement. The explanation is engaging and informative, providing a solid foundation for understanding the physics of springs.

Takeaways
  • 🌟 Hooke's Law states that the restorative force of a spring is equal to -kx, where k is the spring constant and x is the displacement.
  • 📈 The force required to compress a spring increases linearly with the displacement from its natural length.
  • 📊 A graph of the force of compression versus displacement is a straight line with a slope equal to the spring constant k.
  • 🔄 When compressing the spring, the force applied must overcome the spring's restorative force gradually.
  • 🏆 The work done in compressing a spring is proportional to the displacement and is represented by the area under the force-displacement graph.
  • 📐 The area under the force-displacement curve can be calculated as 1/2 * k * x^2, which represents the potential energy stored in the spring.
  • 🤹‍♂️ Displacing the spring involves applying a gradually increasing force, not a sudden large force, to avoid the spring accelerating and potentially springing back.
  • 🔽 The direction of displacement (left or right) is not as important as the magnitude of the displacement when considering the force and work done.
  • 📝 The work done to compress or stretch a spring is equivalent to the potential energy stored in the spring at that displacement.
  • 🔧 The concept of work and potential energy in springs can be extended to problems involving the stretching of springs as well as compression.
  • 🎓 Understanding the relationship between force, displacement, work, and potential energy is fundamental to applying these concepts to various problems in physics.
Q & A

  • What is the natural state of the spring mentioned in the script?

    -The natural state of the spring is when it is not being pushed or pulled, and it is stretched out to its original length without any displacement.

  • What is the relationship between the restorative force and the displacement of the spring?

    -The restorative force is given by Hooke's Law, which states that the force (F) is equal to the negative spring constant (K) times the displacement (x), or F = -Kx. This means that the force increases linearly with the displacement.

  • What direction does the force of compression act when compressing the spring to the left?

    -The force of compression acts to the left, in the same direction as the displacement, to compress the spring.

  • How does the force required to compress the spring change as the spring is compressed further?

    -As the spring is compressed further, the force required increases proportionally to the displacement, following the linear relationship described by Hooke's Law (F = Kx).

  • What is the relationship between the work done to compress the spring and the potential energy stored in it?

    -The work done to compress the spring is equal to the potential energy stored in the spring. This is given by the formula for work, which is the force times the displacement (W = Fx), and for a spring, this becomes W = 1/2Kx^2.

  • What is the formula for calculating the work done to compress or stretch a spring?

    -The work done to compress or stretch a spring is given by the formula W = 1/2Kx^2, where K is the spring constant and x is the displacement from the spring's natural length.

  • How does the graph of force versus displacement for a spring look like?

    -The graph of force versus displacement for a spring is a straight line with a slope equal to the spring constant (K), where the x-axis represents the displacement and the y-axis represents the force of compression or restorative force.

  • What is the area under the force-displacement graph, and what does it represent?

    -The area under the force-displacement graph represents the work done to compress or stretch the spring, which is also the amount of potential energy stored in the spring once it is displaced.

  • How does the potential energy stored in a spring change if the spring constant or the displacement changes?

    -The potential energy stored in a spring, given by the formula U = 1/2Kx^2, is directly proportional to both the spring constant (K) and the square of the displacement (x). If either K or x increases, the potential energy will also increase.

  • What is the significance of the spring constant (K) in the context of the spring's behavior?

    -The spring constant (K) is a measure of the spring's stiffness. A higher K value means the spring is stiffer and requires more force to cause the same displacement, resulting in a steeper slope on the force-displacement graph.

  • How can the work done to compress a spring be visualized?

    -The work done to compress a spring can be visualized as the area under the force-displacement graph. For a linear spring, this area is a triangle, and the work is calculated as 1/2 times the base (displacement x) times the height (Kx), leading to the formula W = 1/2Kx^2.

Outlines
00:00
🌱 Introduction to Spring Mechanics

This paragraph introduces the concept of a spring's natural state and its behavior when subjected to external forces. It explains how a spring behaves when compressed or stretched, focusing on the displacement (x) and the force applied. The key concept introduced here is Hooke's Law, which states that the restorative force of a spring is equal to the negative product of its spring constant (K) and the displacement. The speaker aims to graph the force applied at different points as the spring is compressed, to understand the relationship between force and displacement. The paragraph emphasizes the importance of magnitude over direction in this context and sets the stage for a deeper exploration of the work done in compressing the spring.

05:02
📈 Calculating Work and Potential Energy in Springs

In this paragraph, the speaker delves into the concept of work done in compressing a spring and how it relates to potential energy. The force-displacement graph from the previous discussion is used to approximate the work done, which is visualized as the area under the curve. The speaker explains that work is the product of the force applied and the displacement, and uses the concept of rectangles to approximate this area. The paragraph introduces the idea of integral calculus in the context of calculating work, although it does not delve deeply into the mathematical details. The key takeaway is the formula for the work done to compress the spring (1/2Kx^2) and how it equates to the potential energy stored in the spring. This relationship is demonstrated with an example, where a spring with a spring constant of 10 and compressed by 5 meters stores 125 joules of potential energy.

Mindmap
Keywords
💡Spring
A spring is a mechanical device that is capable of storing energy and works by elastic deformation. In the video, the spring is the central object of study, with its behavior under compression and extension being analyzed. The spring's natural state, its displacement, and the forces acting upon it are key to understanding the potential energy stored within it.
💡Displacement
Displacement refers to the change in position of an object. In the context of the video, it specifically relates to the distance by which the spring is compressed or stretched from its natural state. Displacement is a vector quantity, meaning it has both magnitude and direction, but for the purposes of the video, only the magnitude is considered.
💡Hooke's Law
Hooke's Law is a fundamental principle in physics that states that the force (F) needed to extend or compress a spring by some distance (x) is proportional to that distance, with the proportionality constant being the spring's stiffness, or spring constant (K). Mathematically, it is represented as F = -kx. The negative sign indicates that the force exerted by the spring (restorative force) is in the opposite direction to the displacement. In the video, Hooke's Law is used to calculate the force exerted by the spring at different points of compression or extension.
💡Spring Constant (K)
The spring constant, often denoted as K, is a measure of a spring's stiffness. It indicates the amount of force needed to compress or extend the spring by a unit distance. A higher K value means the spring is stiffer and requires more force to cause the same displacement. In the video, the spring constant is crucial for determining the force exerted by the spring and the potential energy stored within it when compressed or stretched.
💡Restorative Force
The restorative force is the force exerted by a spring to return to its natural, equilibrium position after being displaced. In the video, this force is described as acting in opposition to the displacement, with the magnitude being proportional to the displacement according to Hooke's Law. The restorative force is what allows a spring to store potential energy when it is compressed or stretched.
💡Work
In physics, work is a measure of energy transfer that occurs when a force is applied over a distance. It is calculated as the product of the force applied and the displacement in the direction of the force. In the context of the video, work is done on the spring when force is applied to compress or stretch it, and this work is converted into potential energy stored within the spring.
💡Potential Energy
Potential energy is the stored energy an object has due to its position or condition. In the case of a spring, the potential energy is stored as a result of the spring being compressed or stretched. The amount of potential energy is directly related to the work done on the spring and is given by the formula 1/2Kx^2, where K is the spring constant and x is the displacement of the spring.
💡Compression
Compression refers to the act of pressing two or more objects together, reducing the space between them. In the video, the spring is compressed by applying a force, which leads to a displacement from its natural state. The force required for compression increases linearly with the displacement, as described by Hooke's Law.
💡Graph
A graph is a visual representation of data or mathematical functions. In the video, a graph is used to illustrate the relationship between the force of compression and the displacement of the spring. The graph is a straight line with a slope equal to the spring constant, K, demonstrating the linear relationship between force and displacement.
💡Force
Force is any action that, when unopposed, will change the motion of an object. In the context of the video, force is applied to compress or stretch the spring, and the force exerted by the spring in response (restorative force) is described by Hooke's Law. The force is a key factor in calculating the work done on the spring and the potential energy stored within it.
💡Integral Calculus
Integral calculus is a branch of mathematics that deals with the calculation of quantities, such as area, volume, and other integrals. In the video, the concept of integral calculus is briefly mentioned in relation to calculating the work done on the spring, which is analogous to finding the area under the force-displacement curve. The work done is represented as the area of a triangle in this case, but the general principle extends to more complex shapes and areas in integral calculus.
Highlights

The concept of a spring's natural state and its displacement are introduced, with a focus on the spring being stretched and compressed.

The application of Hooke's Law to determine the restorative force of a spring, which is the force applied by the spring to return to its natural state.

The relationship between the force of compression and the displacement of the spring, with the force being proportional to the displacement.

A graphical representation of the force applied to the spring as a function of its displacement, illustrating the linear relationship.

The process of gradually increasing force to compress the spring, emphasizing the incremental nature of the applied force.

The concept of work done in compressing the spring, relating it to the area under the force-displacement graph.

The definition of work in the context of compressing a spring, which is the product of the force applied and the displacement.

The approximation of work as the sum of the areas of rectangles under the force-displacement graph, touching on the concept of integral calculus.

The calculation of the work done to compress the spring, resulting in the formula of 1/2Kx^2, where K is the spring constant and x is the displacement.

The connection between the work done on the spring and the potential energy stored in it, highlighting their equivalence.

The practical application of the formula in determining the potential energy in a spring with given spring constant and displacement.

The mention of the units for work and potential energy, which are joules, emphasizing the physical significance of the calculations.

The potential for future exploration of problems involving potential energy in springs, setting the stage for further learning.

The importance of understanding the derivation of the formula rather than just memorizing it, for a deeper comprehension of the concepts.

Transcripts

Browse More Related Video

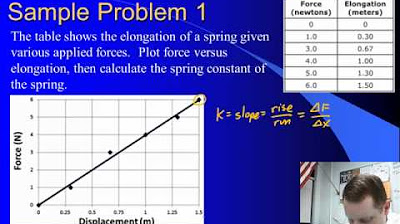
High School Physics - Springs and Hooke's Law

(previous version) Introduction to Elastic Potential Energy with Examples

Intro to springs and Hooke's law | Work and energy | Physics | Khan Academy

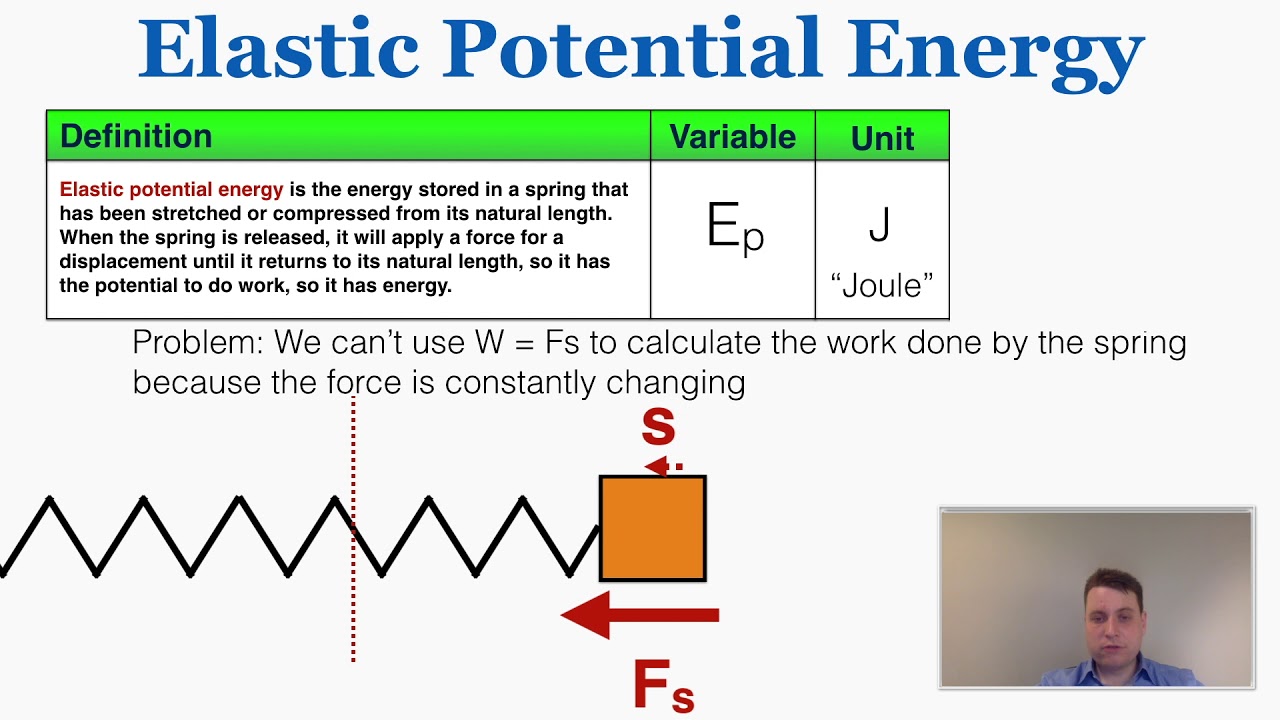
Elastic Potential Energy - IB Physics

Hooke's Law and Elastic Potential Energy

GCSE Physics - Elastic Potential Energy and F = ke Equations #45

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Hooke's LawSpring CompressionPotential EnergyPhysics TutorialMechanical WorkForce GraphDisplacement CalculationEnergy StorageLinear SystemsMathematical Modeling