PreCalculus - Matrices & Matrix Applications (23 of 33) Finding the Inverse of a 3x3 Matrix

Michel van Biezen
12 Jul 201510:57
EducationalLearning
32 Likes 10 Comments

TLDRThis video tutorial from Electron Line introduces the method of finding the inverse of a 3x3 matrix using Gaussian elimination. The process begins by augmenting the matrix with the identity matrix and applying step-by-step row operations to transform the left side into the identity matrix, which in turn transforms the right side into the inverse of the original matrix. Through detailed examples, the instructor demonstrates each operation required to achieve zeros and ones in strategic positions, ultimately leading to the derivation of the inverse matrix. This method, while meticulous, is crucial for ensuring accuracy in mathematical computations involving matrices.

Takeaways
  • 🌟 The video outlines the process of finding the inverse of a 3x3 matrix using the jungle method and Gaussian elimination.
  • 📌 The initial step is to augment the given matrix with the identity matrix.
  • 🔄 The goal of the process is to transform the left side of the augmented matrix into the identity matrix, which turns the right side into the inverse of the original matrix.
  • 📈 The first row is normalized to have a 1 in the first position by multiplying the entire row by 1/2.
  • 🚫 Zeros below the first 1 are created by using row operations to manipulate the second and third rows.
  • 🔢 The process involves turning each diagonal element into a 1 by using appropriate row operations and dealing with the resulting fractions.
  • 🔄 After achieving diagonal ones, the off-diagonal elements in the corresponding rows and columns are turned into zeros using similar row operations.
  • 💡 The video emphasizes the importance of careful calculation as a single mistake can lead to incorrect results.
  • 🔍 To verify the correctness of the calculated inverse, the original matrix is multiplied by its inverse, which should result in the identity matrix.
  • 📝 The script serves as a step-by-step guide for those learning matrix inversion, highlighting the potential for errors and the need for verification.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is finding the inverse of a 3x3 matrix using the Gaussian method of elimination.

  • What is the first step in applying the Gaussian method to find the inverse of a matrix?

    -The first step is to augment the matrix with the identity matrix and then use the Gaussian elimination method to turn the left side of the matrix into the identity matrix.

  • How does the video demonstrate the process of making the first element of the matrix 1?

    -The video demonstrates this by multiplying the first row by 1/2, resulting in a new first row with elements (1/2, a/2, 1).

  • What is the purpose of using the Gaussian elimination method in this context?

    -The purpose of using the Gaussian elimination method is to transform the left side of the augmented matrix into the identity matrix, which in turn transforms the right side into the inverse of the original matrix.

  • How does the video ensure that the first column, except for the first element, has zeros?

    -The video uses row operations, specifically adding and subtracting multiples of rows, to eliminate the elements in the first column below the first element.

  • What is the significance of having ones across the diagonal of the matrix after certain steps in the process?

    -Having ones across the diagonal is significant because it indicates progress towards the identity matrix, which is the goal of the Gaussian elimination method when finding the inverse of a matrix.

  • How does the video verify the correctness of the matrix inverse?

    -The video suggests verifying the correctness by multiplying the original matrix with its inverse and checking if the result is the identity matrix.

  • What is a common mistake that can occur during the Gaussian elimination process?

    - A common mistake is making a single error that can lead to incorrect results, often manifesting as numbers becoming very large or very small fractions, indicating that a step may need to be redone.

  • How does the video address the challenge of the lengthy process of finding the inverse of a matrix?

    -The video acknowledges the lengthiness and the potential for error, advising that if an error is suspected, one may consider starting over to avoid further mistakes.

  • What is the final result of the inverse matrix as presented in the video?

    -The final result of the inverse matrix is a matrix with elements (-4, -5, 4; 1, 1, -1; 5, 4, -6).

  • What is the advice given in the video for dealing with errors in the Gaussian elimination process?

    -The advice given is to carefully check each step and if a mistake is suspected, to start over to avoid further errors and to use the check of multiplying by the original matrix to confirm correctness.

Outlines
00:00
📚 Introduction to Finding the Inverse of a 3x3 Matrix

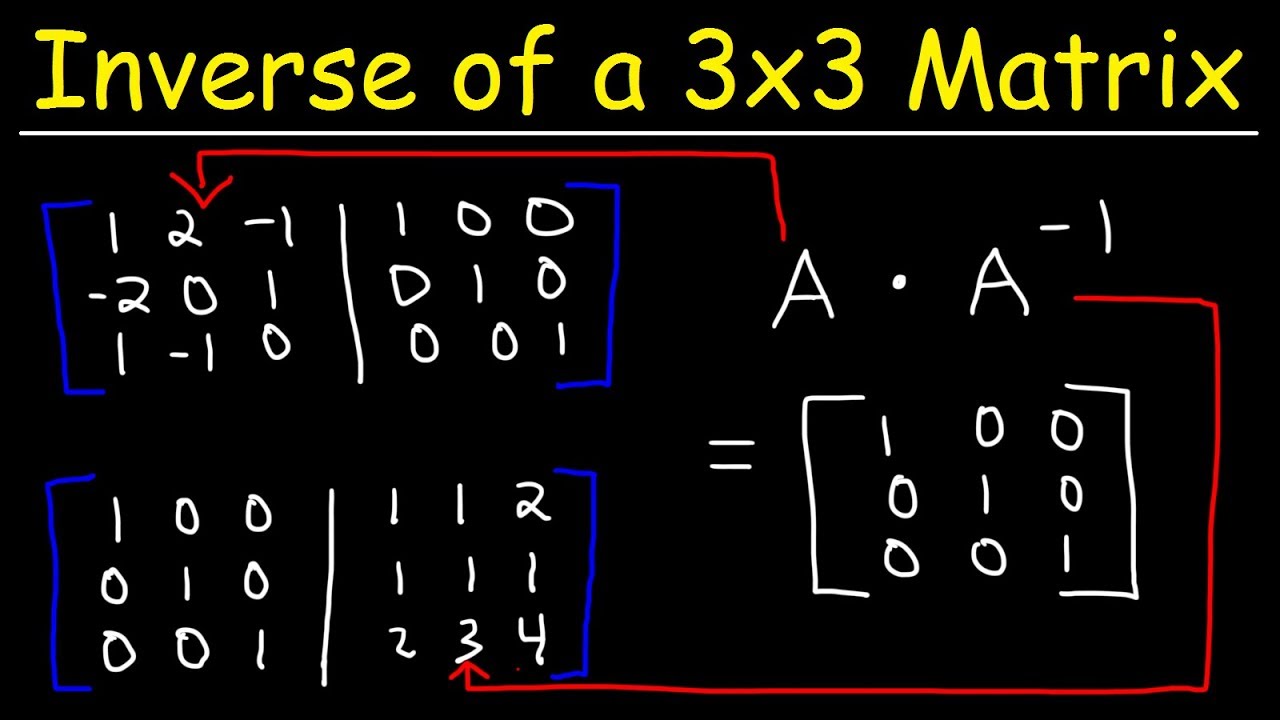
This paragraph introduces the topic of finding the inverse of a 3x3 matrix using the jungle method. The process begins with augmenting the given matrix with the identity matrix and then applying the Gaussian elimination method to transform the left side of the augmented matrix into the identity matrix, resulting in the right side being the inverse of the original matrix. The first step is to scale the first row to make the first element a 1, followed by using that row to turn the corresponding elements in the second and third rows into 0. The paragraph provides a detailed explanation of the calculations and the resulting matrix after each step.

05:01
🔢 Elimination Steps for Matrix Inversion

In this paragraph, the video script delves into the specifics of the elimination process for finding the inverse of a matrix. It describes how to manipulate the rows to achieve a 1 in certain positions and 0 in others, using operations like addition and subtraction of multiples of rows. The paragraph emphasizes the importance of precision in calculations, as even small errors can lead to incorrect results. It also provides a method to check the correctness of the inverse by multiplying the original matrix with its inverse to obtain the identity matrix.

10:03
🚫 Pitfalls and Verification of Matrix Inversion

The final paragraph of the script highlights common pitfalls when finding the inverse of a matrix, such as making a single mistake that can lead to an entirely incorrect outcome. It warns viewers about the consequences of errors, such as the appearance of large fractions and nonsensical results. The paragraph concludes with advice on how to verify the calculated inverse, suggesting that multiplying the original matrix with the computed inverse should yield the identity matrix. If this is not the case, it indicates a mistake in the process, and it may be necessary to start over.

Mindmap
Keywords
💡inverse of a matrix
The inverse of a matrix is a fundamental concept in linear algebra. It is a matrix that, when multiplied with the original matrix, results in the identity matrix. In the context of the video, the inverse is calculated for a 3x3 matrix using the Gaussian elimination method. The process involves transforming the original matrix into its inverse through a series of row operations.
💡jungle method
The jungle method, as mentioned in the video, is a colloquial term for the process of finding the inverse of a matrix. It involves a series of complex steps that can be likened to navigating through a dense jungle, hence the name. The method requires careful application of mathematical techniques like Gaussian elimination to ensure that no errors are made in the process.
💡Gaussian elimination
Gaussian elimination is a systematic way to solve linear equations by reducing the coefficient matrix to a simpler form, known as row echelon form, through a series of row operations. In the video, this method is used to find the inverse of a 3x3 matrix by transforming it into the identity matrix through these operations.
💡identity matrix
An identity matrix is a special square matrix with ones on the diagonal and zeros elsewhere. When multiplied by any matrix of the same dimension, the original matrix is returned. In the video, the identity matrix is the target form that the left side of the augmented matrix is transformed into during the process of finding the inverse.
💡row operations
Row operations are the fundamental steps used in Gaussian elimination to manipulate the rows of a matrix. These operations include swapping rows, multiplying a row by a scalar, and adding or subtracting one row from another. They are essential for transforming the matrix to achieve the desired result, such as finding the inverse.
💡augmented matrix
An augmented matrix is a combination of two matrices, typically placed side by side, where one is the original matrix and the other is the identity matrix. It is used in the process of finding the inverse of a matrix, as it allows the application of row operations on both matrices simultaneously, leading to the solution.
💡linear equations
Linear equations are mathematical equations in which the variables are to the first power (i.e., no products or ratios of the variables). Gaussian elimination, including the method described in the video, is often used to solve systems of linear equations, which involve multiple such equations simultaneously.
💡row echelon form
Row echelon form is a specific arrangement of a matrix where the rows are manipulated to create a 'staircase' of zeros below the main diagonal. This form of the matrix simplifies the process of solving linear equations and finding the inverse, as it brings the matrix closer to the identity matrix.
💡error checking
Error checking is the process of verifying the accuracy of a solution or calculation. In the context of the video, it refers to the importance of ensuring that the steps taken to find the inverse of a matrix are correct, as a single mistake can lead to an incorrect result.
💡matrix multiplication
Matrix multiplication is the process of multiplying two matrices together to produce a third matrix. It is a fundamental operation in linear algebra with specific rules that dictate how the elements of the resulting matrix are calculated. In the video, the product of the original matrix and its inverse should result in the identity matrix, confirming the correctness of the inverse.
Highlights

The video demonstrates the application of the jungle method for finding the inverse of a 3x3 matrix. (Start time: 0s)

The process begins by augmenting the matrix with the identity matrix. (Start time: 10s)

Gaussian elimination is used to transform the left side of the augmented matrix into the identity matrix. (Start time: 15s)

The inverse of the matrix is obtained when the left side becomes the identity matrix, with the right side transforming into the inverse. (Start time: 20s)

The first step in the process involves making the first diagonal element 1 by scaling the first row. (Start time: 30s)

Subsequent steps use row operations to create zeros in specific positions in the matrix. (Start time: 40s)

The video emphasizes the importance of accuracy in calculations to avoid errors that can lead to incorrect results. (Start time: 50s)

The process of turning each diagonal element into 1 involves careful row operations and fraction calculations. (Start time: 1m)

The video provides a detailed explanation of how to manipulate each row to achieve the desired zero or one in the matrix. (Start time: 1m 30s)

The video highlights the use of negative numbers and fractions in the Gaussian elimination process. (Start time: 2m)

The final result of the process is the inverse of the original matrix, which can be verified by multiplying it with the original matrix to obtain the identity matrix. (Start time: 2m 30s)

The video serves as a practical guide for those learning matrix inversion using the Gaussian elimination method. (Start time: 3m)

The process is shown to be meticulous and requires attention to detail to avoid common mistakes. (Start time: 3m 30s)

The video provides a clear and step-by-step approach to finding the inverse of a 3x3 matrix, which is beneficial for educational purposes. (Start time: 4m)

The video concludes by reiterating the importance of accuracy and the method to verify the correctness of the obtained inverse matrix. (Start time: 4m 30s)

Transcripts

Browse More Related Video

Inverse of a 3x3 Matrix

PreCalculus - Matrices & Matrix Applications (22 of 33) Using Gaussian Elimin. to Find the Inverse

Classic video on inverting a 3x3 matrix part 2 | Matrices | Precalculus | Khan Academy

PreCalculus - Matrices & Matrix Applications (28 of 33) Solving Sys of Linear Eqn with Inverse

Inverse of a 3x3 Matrix | Co-factor Method

Inverse Matrices and Their Properties

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Matrix InversionGaussian EliminationLinear AlgebraMathematics TutorialInverse Calculation3x3 MatrixEducational VideoMath TipsMatrix TricksAlgebra Techniques