Inverse of a 3x3 Matrix | Co-factor Method

IQ Initiative
4 Dec 202213:54
EducationalLearning
32 Likes 10 Comments

TLDRThis video tutorial walks viewers through the process of finding the inverse of a 3x3 matrix using the cofactor method. It begins by explaining the prerequisites, such as understanding determinants and matrix transposition. The video then demonstrates how to calculate the determinant of the given matrix and proceeds to detail each step in creating the cofactors. By using the pattern of positive and negative signs, the method involves forming 2x2 matrices and calculating their determinants to obtain the cofactors. The video further illustrates transposing the cofactor matrix to get the adjoint matrix and finally, using the adjoint and determinant to calculate the inverse matrix. The step-by-step guide is designed to be educational and easy to follow, ensuring that viewers can effectively apply the cofactor method to find the inverse of a 3x3 matrix.

Takeaways
  • 📌 The video outlines the process of finding the inverse of a 3x3 matrix using the cofactor method.
  • 🔍 Understanding determinants and matrix transposition is essential before applying the cofactor method.
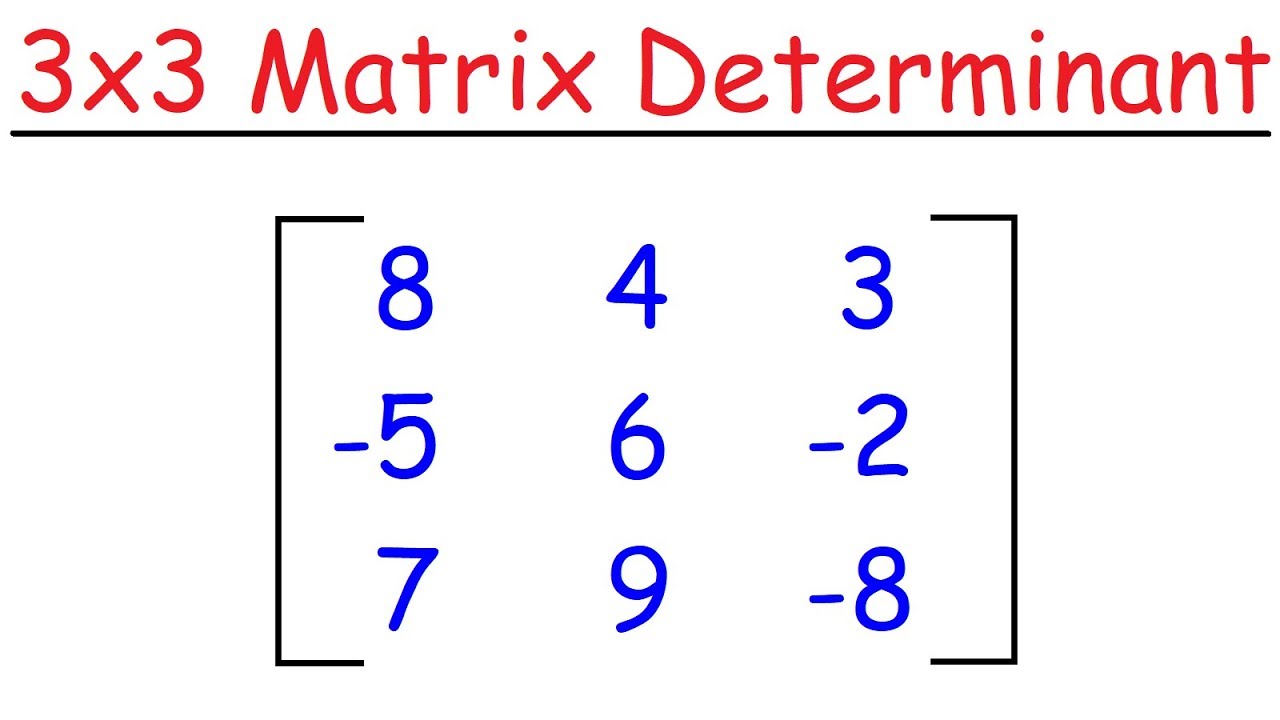
  • 🧩 The first step in the process is to calculate the determinant of the given 3x3 matrix.
  • 🔢 The determinant is computed by forming and solving 2x2 matrix determinants from the larger matrix.
  • 🌟 The video provides a clear example of how to compute the determinant, resulting in a positive value of 18.
  • 🎭 The concept of cofactors is introduced, which are derived from the original matrix based on a specific pattern of signs.
  • 🔄 To find the adjoint matrix, the cofactors are transposed, resulting in a matrix with specific sign patterns.
  • 🖥️ The adjoint matrix is used in conjunction with the determinant to find the inverse matrix.
  • 🛠️ The inverse matrix is calculated by dividing each element of the adjoint matrix by the determinant (18 in this case).
  • 📈 The final inverse matrix is presented in a simplified form, with each element reduced to its simplest fraction.
  • 📚 The video emphasizes the cofactor method as an effective approach to finding the inverse of a 3x3 matrix, alongside mentioning alternative methods like row operations.
Q & A

  • What is the core method discussed in the video for finding the inverse of a 3x3 matrix?

    -The core method discussed in the video is the cofactor method, which involves finding the determinant of the matrix, creating cofactors, and then transposing the cofactor matrix to find the adjoint, which can be used to calculate the inverse matrix.

  • What are the preliminary steps required before using the cofactor method?

    -Before using the cofactor method, one needs to know how to find the determinant of a 3x3 matrix and how to transpose a matrix, as these concepts are fundamental to the procedure.

  • How is the determinant of the given 3x3 matrix computed in the video?

    -The determinant is computed by first inserting a positive, negative, positive pattern into the matrix, then forming 2x2 matrices by excluding the corresponding row and column elements, and finally calculating the determinant by summing the products of the elements with their respective signs.

  • What is the significance of the pattern used when computing the determinant of a 3x3 matrix?

    -The pattern of positive, negative, positive is used to determine the signs of the elements in the 2x2 matrices formed during the determinant computation process. This pattern ensures that the correct alternating signs are applied to each minor when calculating the determinant.

  • How are the cofactors of the matrix found according to the video?

    -Cofactors are found by creating 2x2 matrices from the original 3x3 matrix by removing the row and column of each element, calculating the determinant of each 2x2 matrix, and then applying the appropriate sign based on the cofactor's position in the matrix.

  • What does transposing the cofactor matrix give us?

    -Transposing the cofactor matrix gives us the adjoint of the original matrix. The adjoint is a key component in finding the inverse of a matrix using the cofactor method.

  • How is the inverse matrix calculated using the adjoint and the determinant?

    -The inverse matrix is calculated by taking the adjoint of the original matrix and multiplying each element by the reciprocal of the determinant of the original matrix (1 divided by the determinant).

  • What is the final determinant value of the given 3x3 matrix in the video?

    -The final determinant value of the given 3x3 matrix is positive 18.

  • What is the formula for the inverse of a matrix in terms of its adjoint and determinant?

    -The formula for the inverse of a matrix A, denoted as A^(-1), is given by 1/determinant(A) * adjoint(A), where 'determinant(A)' is the determinant of matrix A and 'adjoint(A)' is the transposed cofactor matrix of A.

  • How can the inverse matrix be simplified as shown in the video?

    -The inverse matrix can be simplified by dividing each element by the determinant (18 in this case), which results in the simplified matrix with elements -9/18, 9/18, 18/18, -10/18, -8/18, 4/18, -16/18, 22/18, and 34/18, which further simplify to -1/2, 1/2, 1, -5/9, -4/9, 2/9, -8/9, 11/9, and 17/9 respectively.

  • What alternative method is mentioned in the video for finding the inverse of a matrix?

    -The video mentions that an alternative method for finding the inverse of a matrix is through row operations, although the focus of the video is on the cofactor method.

Outlines
00:00
📚 Introduction to Finding the Inverse of a 3x3 Matrix

This paragraph introduces the topic of finding the inverse of a 3x3 matrix using the cofactor method. It emphasizes the importance of understanding how to calculate the determinant of a matrix and how to transpose a matrix, which are essential concepts for using the cofactor method. The video begins by demonstrating how to find the determinant of a given matrix, explaining the process of inserting positive and negative signs in a specific pattern. The paragraph also mentions the creation of 2x2 matrices from the original 3x3 matrix to compute the determinant, and provides a link in the description for further guidance on this topic.

05:02
🔍 Calculation of Determinants for Cofactor Matrices

In this paragraph, the video script delves into the process of calculating the determinants for the 2x2 matrices that form the cofactors. It explains how to fill in these matrices with values from the original matrix by omitting specific rows and columns. The paragraph provides a step-by-step calculation of the determinants, showing how to perform the necessary arithmetic operations to arrive at the final results. It also describes the formation of a larger matrix to facilitate the calculation of cofactors, emphasizing the pattern of positive and negative signs that dictate which elements are included in each 2x2 submatrix.

10:03
🔄 Transposing the Cofactors and Finding the Inverse Matrix

The final paragraph focuses on transposing the matrix of cofactors to obtain the adjoint matrix and using it, along with the determinant, to find the inverse of the original 3x3 matrix. It explains that the adjoint matrix is simply the transpose of the cofactor matrix and provides the resulting adjoint matrix after transposition. The paragraph then outlines the formula for finding the inverse matrix, which involves dividing each element of the adjoint matrix by the determinant of the original matrix. The video concludes by presenting the final inverse matrix, obtained by applying the cofactor method, and briefly mentions alternative methods such as row operations for finding the inverse of a matrix.

Mindmap
Keywords
💡Inverse of a matrix
The inverse of a matrix is a mathematical concept referring to a matrix that, when multiplied with the original matrix, results in the identity matrix. In the context of this video, the inverse is found using the cofactor method for a 3x3 matrix, which is a key step in solving systems of linear equations and understanding matrix operations.
💡Determinant
The determinant of a square matrix is a scalar value that can be computed from the elements of the matrix and is used to find the invertibility of the matrix. In the video, calculating the determinant is the first step in the cofactor method, as it is necessary to determine if the matrix has an inverse and to normalize the cofactors to find the adjoint matrix.
💡Cofactor
A cofactor of a matrix is the determinant of a smaller matrix obtained by removing one row and one column from the original matrix. In the video, the cofactors are calculated for each element of the 3x3 matrix and are used to construct the adjoint matrix, which is essential for finding the inverse of the matrix.
💡Adjoint matrix
The adjoint matrix, also known as the adjugate matrix, is the transpose of the cofactor matrix of a square matrix. It plays a crucial role in finding the inverse of a matrix, as the inverse can be calculated by multiplying the adjoint matrix by the reciprocal of the determinant.
💡Matrix transpose
Transposing a matrix involves interchanging the rows and columns of the matrix to create a new matrix. This operation is necessary when finding the adjoint matrix, which is the transpose of the cofactor matrix, and is used in the process of calculating the inverse of a matrix.
💡Matrix of cofactors
A matrix of cofactors is a matrix where each element is replaced by its corresponding cofactor. This matrix is used to calculate the adjoint matrix and, subsequently, the inverse of the original matrix when the determinant is non-zero.
💡Submatrix
A submatrix is a smaller matrix derived from a larger matrix by removing one or more rows and/or columns. In the context of the video, submatrices are used to calculate the determinants that form the cofactors for the original matrix.
💡Linear equations
Linear equations are mathematical equations in which the variables have a degree of 1. The concept is related to the video's content because one of the applications of finding the inverse of a matrix is to solve systems of linear equations, which can have multiple unknowns.
💡Row operations
Row operations are a set of operations performed on the rows of a matrix, such as swapping rows, multiplying a row by a scalar, or adding a multiple of one row to another. These operations are used in various matrix manipulations, including finding the inverse of a matrix, as an alternative to the cofactor method demonstrated in the video.
💡Identity matrix
An identity matrix is a special square matrix with ones on the diagonal and zeros elsewhere. When multiplied by another matrix, the identity matrix leaves the other matrix unchanged. The product of a matrix and its inverse is the identity matrix, which is a fundamental property used to verify the correctness of the inverse matrix calculation.
Highlights

Introduction to finding the inverse of a three by three matrix using the cofactor method.

Understanding the prerequisites for using the cofactor method, such as knowing how to find the determinant and transpose a matrix.

Step-by-step explanation of computing the determinant of a three by three matrix with specific examples.

Detailed calculation of the determinant involving the formation and computation of two by two matrices.

Explanation of the cofactor matrix and its significance in the process of finding the inverse.

Demonstration of how to create and sign the cofactor matrix correctly based on the rules of positive and negative signs.

Formation of two by two matrices for each cofactor by removing specific rows and columns from the original matrix.

Comprehensive calculation of the cofactors by finding the determinants of the smaller two by two matrices.

Transposing the cofactor matrix to obtain the adjoint matrix, which is a key step in the process.

Explanation of how the adjoint matrix and the determinant are used to find the inverse matrix.

Presentation of the final formula for calculating the inverse of a matrix using the adjoint and determinant.

Clear and concise computation of the inverse matrix using the cofactor method.

Comparison of the cofactor method to other methods like row operations for finding the matrix inverse.

Summary of the video's content and the practical application of the cofactor method in matrix inversion.

Transcripts

Browse More Related Video

Inverse of a 3x3 Matrix - (THE SIMPLE WAY)

How to find The Inverse of a (3 × 3) matrix Using Determinant and Co-factor

How to find the Inverse of a Matrix

How to Invert Matrices - Exercises (Step by Step)

How To Find The Determinant of a 3x3 Matrix

Inverting 3x3 part 1: Calculating matrix of minors and cofactor matrix | Precalculus | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Matrix InversionCofactor MethodLinear AlgebraMathematics Tutorial3x3 MatrixDeterminant CalculationMatrix TranspositionEducational ContentMath VideoIn-Depth Explanation