Inverse of a 3x3 Matrix - (THE SIMPLE WAY)

IQ Initiative
18 Jun 202315:14
EducationalLearning
32 Likes 10 Comments

TLDRThe video script outlines a step-by-step process for finding the inverse of a 3x3 matrix using the cofactor method. It begins by explaining how to calculate the determinant, followed by the creation of 2x2 matrices to find cofactors. The script emphasizes the importance of sign patterns in the matrix and demonstrates how to transpose the cofactor matrix to obtain the adjoint. Finally, it shows how to use the determinant and adjoint to compute the inverse matrix, providing a clear and detailed explanation suitable for learners.

Takeaways
  • 📌 The video explains the process of finding the inverse of a 3x3 matrix using the cofactor method.
  • 🔍 The first step is to calculate the determinant of the given matrix, which is a crucial part of the process.
  • 🧩 To find the determinant, the script outlines the process of forming 2x2 matrices by excluding the row and column of each element in the 3x3 matrix.
  • 🔢 The determinant is calculated by multiplying the elements of the 2x2 matrices and combining them with appropriate signs based on the position of the element.
  • 🌟 Once the determinant is found, the next step is to calculate the cofactors for each element in the matrix.
  • 🥂 Cofactors are found by creating 2x2 matrices for each element, similar to the process of finding the determinant, but excluding the row and column of the specific element.
  • 🔄 After finding the cofactors, they are transposed to form the adjoint matrix, which is a key component in finding the inverse.
  • 📈 The adjoint matrix is obtained by transposing the matrix of cofactors, swapping rows for columns and vice versa.
  • 📊 The inverse of the matrix is then found by multiplying the adjoint matrix by the reciprocal of the determinant.
  • 👉 The final step is to simplify the resulting matrix by reducing fractions where possible to obtain the inverse matrix.
  • 💡 The video provides a detailed, step-by-step guide that can be followed to find the inverse of any 3x3 matrix using the cofactor method.
Q & A

  • What is the primary method used in the script to find the inverse of a 3x3 matrix?

    -The primary method used in the script to find the inverse of a 3x3 matrix is the cofactor method.

  • What is the first step in finding the inverse of a matrix?

    -The first step in finding the inverse of a matrix is to calculate the determinant of the matrix.

  • How is the determinant of a 3x3 matrix calculated according to the script?

    -The determinant of a 3x3 matrix is calculated by setting up a plus-minus-plus or minus-plus-minus pattern and finding the determinants of the resulting 2x2 matrices formed by excluding the row and column of each element, then summing them up with appropriate signs.

  • What are cofactors in the context of matrix inversion?

    -Cofactors are the determinants of the 2x2 matrices formed by removing the row and column of each element in the original matrix. They are used to find the adjoint of the matrix, which is a key step in the matrix inversion process.

  • How is the adjoint of a matrix found according to the script?

    -The adjoint of a matrix is found by calculating the cofactors for each element in the matrix and then transposing the resulting matrix (swapping rows for columns).

  • What is the formula used to find the inverse of a matrix?

    -The formula used to find the inverse of a matrix is the inverse of a matrix (A) equals to 1 over the determinant of A multiplied by the adjoint of A.

  • How does the sign pattern affect the cofactors in a 3x3 matrix?

    -The sign pattern affects the cofactors in a 3x3 matrix by alternating between plus and minus signs. The pattern is plus-minus-plus, minus-plus-minus, etc., and this determines whether the cofactor is positive or negative.

  • What does the determinant tell us about a matrix?

    -The determinant of a matrix tells us several things. If the determinant is zero, the matrix does not have an inverse and is singular. If it is non-zero, the matrix is invertible and has a unique inverse.

  • What happens if the determinant of a matrix is zero?

    -If the determinant of a matrix is zero, the matrix is singular, meaning it does not have an inverse. This is because the rows (or columns) of the matrix are linearly dependent.

  • What is the significance of transposing the matrix of cofactors?

    -Transposing the matrix of cofactors is necessary to find the adjoint of the original matrix. The adjoint matrix is crucial for calculating the inverse of the original matrix using the formula involving the determinant and the adjoint.

  • How can we simplify the final result when finding the inverse of a matrix?

    -We can simplify the final result when finding the inverse of a matrix by reducing fractions where possible, canceling common factors, and simplifying expressions to make the matrix easier to read and understand.

  • What is the role of the cofactor method in linear algebra?

    -The cofactor method is a fundamental technique in linear algebra for finding the inverse of a matrix. It is particularly useful for matrices that are not easily invertible through other simpler methods, such as 2x2 matrices or matrices with a lot of zeros.

Outlines
00:00
📚 Introduction to Finding the Inverse of a 3x3 Matrix

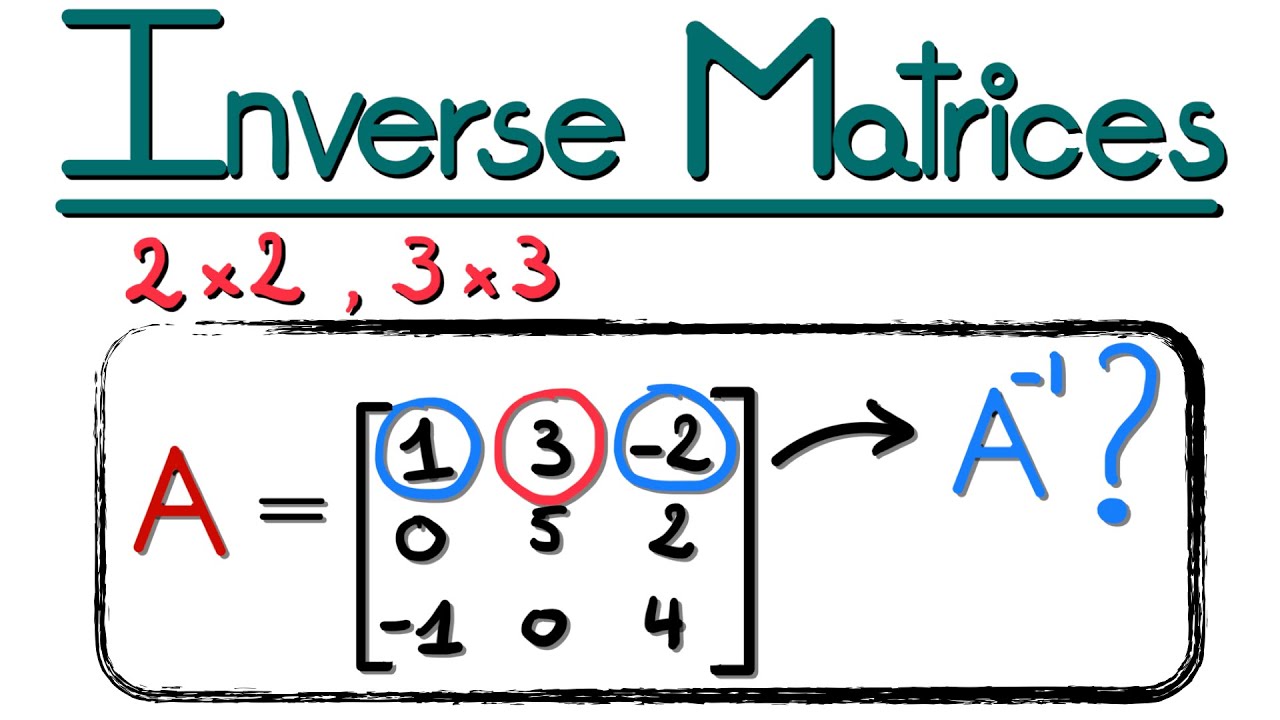
This paragraph introduces the process of finding the inverse of a 3x3 matrix using the cofactor method. It begins by explaining the need to first calculate the determinant of the matrix. The speaker then demonstrates how to find the determinant by setting up a specific pattern of plus and minus signs, and calculating the values in the specified row to form a 2x2 matrix. The determinant is calculated by finding the product of the values in the 2x2 matrices formed by excluding the row and column of each element in the original matrix. The paragraph concludes with the determinant value of the given matrix, which is found to be 30.

05:00
🔍 Calculating Cofactor Matrices and Determinants

In this paragraph, the speaker continues the process of finding the inverse of the matrix by explaining how to calculate the cofactors. Each cofactor is found by creating a 2x2 matrix from the original 3x3 matrix by removing the row and column of a chosen element. The determinant of each 2x2 matrix is then calculated, taking into account the pattern of plus and minus signs based on the position of the element in the original matrix. The paragraph details the calculations for each cofactor, leading to a complete set of cofactors for the matrix.

10:02
🔧 Transposing Cofactors to Find the Adjoint and Inverse

The final step in finding the inverse of the matrix is transposing the cofactor matrix to obtain the adjoint. This paragraph explains the process of transposing, where the rows become columns and vice versa. The adjoint matrix is then used in conjunction with the determinant to find the inverse of the original matrix. The formula for the inverse is presented, and the speaker demonstrates the calculation by multiplying the adjoint matrix by the reciprocal of the determinant. The final inverse matrix is presented in a simplified form, completing the process of finding the inverse of the given 3x3 matrix.

Mindmap
Keywords
💡Inverse of a Matrix
The inverse of a matrix is a mathematical concept that refers to finding a matrix that, when multiplied with the original matrix, results in the identity matrix. This process is crucial in solving systems of linear equations and understanding the properties of linear transformations. In the video, the main goal is to find the inverse of a 3x3 matrix using the cofactor method, which involves calculating the determinant and then the adjoint of the matrix.
💡Determinant
The determinant of a matrix is a scalar value that can be computed from the elements of a square matrix. It is an important concept in linear algebra and has various applications, such as determining the invertibility of a matrix. A non-zero determinant indicates that the matrix has an inverse. In the video, the first step in finding the inverse of a matrix is to calculate its determinant, which is done by setting up a series of 2x2 matrices and evaluating their determinants.
💡Cofactor
A cofactor of a matrix is the determinant of a smaller matrix obtained by removing one row and one column from the original matrix, multiplied by (-1)^(i+j), where i and j are the row and column indices of the element. Cofactor matrices play a key role in calculating the inverse and adjoint of a matrix. In the video, the process of finding the cofactors involves creating 2x2 matrices from the original 3x3 matrix by removing the row and column of each element and then calculating their determinants.
💡Adjoint Matrix
The adjoint matrix, also known as the adjugate matrix, is the transpose of the cofactor matrix of a square matrix. It is a crucial component in the formula for finding the inverse of a matrix. The adjoint matrix has the property that its product with the original matrix results in a diagonal matrix with the determinant of the original matrix on the diagonal. In the video, the adjoint matrix is obtained by transposing the matrix of cofactors, which is then used in the formula to compute the inverse of the original matrix.
💡Matrix Transpose
Transposing a matrix involves interchanging the rows and columns of the matrix to create a new matrix. This operation is essential in various mathematical processes, including finding the adjoint matrix, which is a step in calculating the inverse of a matrix. In the video, the process of transposing the cofactor matrix is demonstrated to obtain the adjoint matrix, which is then used in the formula for the inverse.
💡Linear Equations
Linear equations are mathematical equations in which the relationship between variables is linear, meaning they can be expressed in the form of a straight line when plotted on a graph. The concept of matrix inversion is closely related to solving systems of linear equations, as the inverse of a matrix can be used to find the unique solution to such a system if it exists. The video's focus on finding the inverse of a matrix is directly related to the broader context of solving linear equations.
💡Cofactor Method
The cofactor method is a technique used to calculate the inverse of a matrix. It involves finding the determinant of the matrix, computing the cofactors for each element, forming the adjoint matrix, and then using these to find the inverse. The method is particularly useful for square matrices and is the primary focus of the video, where each step is explained in detail.
💡Identity Matrix
An identity matrix is a special square matrix with ones on the diagonal and zeros elsewhere. It is the multiplicative identity for matrix multiplication, meaning that any matrix multiplied by the identity matrix results in the original matrix. The inverse of a matrix, when it exists, is used to obtain the identity matrix when multiplied by the original matrix. This concept is central to the video's discussion on matrix inversion.
💡Linear Transformation
A linear transformation is a function that maps vectors from one vector space to another while preserving the operations of vector addition and scalar multiplication. Matrices can represent linear transformations, and the inverse of a matrix can be used to reverse or 'undo' a linear transformation. The video's focus on matrix inversion is relevant in the context of understanding and manipulating linear transformations.
💡Matrix Multiplication
Matrix multiplication is an operation that takes a pair of matrices and produces a third matrix. The resulting matrix has a number of rows equal to the number of rows of the first matrix and a number of columns equal to the number of columns of the second matrix. The process of finding the inverse of a matrix involves understanding matrix multiplication, as the product of a matrix and its inverse results in the identity matrix.
Highlights

Introduction to finding the inverse of a 3x3 matrix using the cofactor method.

The first step is to find the determinant of the matrix.

Determinant calculation involves setting up a plus-minus-plus pattern and evaluating 2x2 matrices.

The determinant of the matrix is found to be 30.

Next, find the cofactors by creating and evaluating 2x2 matrices for each element in the matrix.

Cofactors are calculated by removing the row and column of the current element and finding the determinant of the remaining 2x2 matrix.

The signs of the cofactors are determined by the pattern plus-minus-plus-minus-plus-minus.

Transpose the matrix of cofactors to get the adjoint of the original matrix.

The adjoint matrix is used to find the inverse of the original matrix.

The formula for the inverse of a matrix is 1/determinant * adjoint matrix.

Substitute the values into the formula to calculate the inverse matrix.

Reduction of fractions in the inverse matrix for simplification.

Final inverse matrix is presented in simplified form.

The process is summarized with a clear explanation of the steps involved in finding the inverse of a matrix.

The video provides a practical guide to understanding matrix inversion through a step-by-step process.

The method can be applied to solve various mathematical problems involving matrices.

Transcripts

Browse More Related Video

Inverse of a 3x3 Matrix | Co-factor Method

How to find the Inverse of a Matrix

How to Invert Matrices - Exercises (Step by Step)

Inverse Matrices and Their Properties

How to find The Inverse of a (3 × 3) matrix Using Determinant and Co-factor

Classic video on inverting a 3x3 matrix part 1 | Matrices | Precalculus | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Matrix InversionCofactor MethodLinear AlgebraMathematics TutorialDeterminant CalculationMatrix TransposeInverse PropertiesMath EducationalMathematics ConceptsAdvanced Math