Classic video on inverting a 3x3 matrix part 1 | Matrices | Precalculus | Khan Academy
TLDRThe video script presents a step-by-step guide on inverting a 3x3 matrix, a tedious process that, while useful for understanding mathematical principles, is typically better suited for a computer. The process involves creating a matrix of minors, converting it to a matrix of cofactors, and then taking the adjugate (adjoint) of the matrix. Finally, the inverse is found by multiplying the adjugate by the reciprocal of the original matrix's determinant. The video emphasizes the importance of careful computation and provides an example to illustrate the method.
Takeaways
- 🧠 Inversion of a 3x3 matrix is a complex and tedious process, often better performed by a computer.
- 😖 The process involves creating a matrix of minors, which is a 3x3 matrix derived from the determinants of the original matrix's minors.
- 🔢 A minor is the determinant of the remaining matrix after removing a row and a column from the original matrix.
- 🏁 The matrix of cofactors is obtained by applying a pattern of plus and minus signs to the matrix of minors.
- 🔄 The adjugate (or adjoint) of a matrix is the transpose of the matrix of cofactors, where rows and columns are switched.
- 🧩 The determinant of a 3x3 matrix is calculated by multiplying each element in a row by its corresponding cofactor and summing the results.
- 🔍 The inverse of a matrix is found by multiplying the adjugate by the reciprocal of the determinant.
- 📈 The script provides a step-by-step example of inverting a specific 3x3 matrix with non-hairy numbers for clarity.
- 👀 The process emphasizes the importance of avoiding careless mistakes when dealing with such computations.
- 📝 The video script serves as a tutorial for those who may need to understand or perform matrix inversion, despite its complexity.
- 💡 The script also mentions that future videos will provide more intuitive explanations and alternative algorithms for matrix inversion.
Q & A
What is the speaker's least favorite computation in mathematics?
-The speaker's least favorite computation in mathematics is inverting a 3 by 3 matrix.
Why does the speaker think it's better for a computer to invert a matrix?
-The speaker believes that it's better for a computer to perform matrix inversion due to the complexity and the high chance of making careless mistakes when doing it manually.
What is the first step in inverting a 3 by 3 matrix?
-The first step in inverting a 3 by 3 matrix is to create a matrix of minors.
What is a minor in the context of matrix inversion?
-A minor is the determinant of the remaining matrix after a row and a column of the original matrix have been eliminated.
What is the pattern for converting a matrix of minors to a matrix of cofactors in a 3 by 3 matrix?
-The pattern for converting a matrix of minors to a matrix of cofactors in a 3 by 3 matrix is plus, minus, plus, minus, plus, minus, plus.
What is the adjugate of a matrix?
-The adjugate of a matrix is the transpose of the matrix of cofactors, where rows and columns are switched.
How is the determinant of a matrix calculated?
-The determinant of a matrix is calculated by multiplying each term in a row (or column) by its corresponding cofactor and summing the results.
What is the inverse of a matrix?
-The inverse of a matrix is another matrix that, when multiplied with the original matrix, results in the identity matrix, provided the original matrix is invertible.
How is the inverse of a matrix calculated?
-The inverse of a matrix is calculated by taking the adjugate of the matrix and multiplying it by 1 over the determinant of the matrix.
What does the speaker suggest as a good exercise for the viewer?
-The speaker suggests multiplying the inverted matrix by the original matrix as a good exercise to ensure that the obtained result is the identity matrix, thereby verifying the correctness of the inversion.
Why does the speaker mention that the process might seem like voodoo?
-The speaker mentions that the process might seem like voodoo because it involves a lot of complex steps and terminology that can be hard to understand without proper intuition, which the speaker promises to provide in future videos.
Outlines
🤔 Inversion of a 3x3 Matrix
The speaker begins by expressing their dislike for inverting a 3x3 matrix, acknowledging that it's a task better suited for a computer but necessary to learn. They introduce the concept of creating a matrix of minors, which involves calculating the determinant of the remaining 2x2 matrix after removing a row and column. The speaker provides a step-by-step explanation of how to find the minor for each element in the original 3x3 matrix, using the example matrix A with elements 1, 0, 0, 2, 1, 1, 1, 1, 1. They emphasize the importance of careful computation to avoid mistakes.
🔢 Calculation of the Matrix of Minors
Continuing from the previous explanation, the speaker illustrates the process of calculating the matrix of minors for the given 3x3 matrix A. They detail the process of finding the determinant for each minor and constructing the matrix by placing these determinants in the corresponding positions. The speaker also clarifies the concept of a minor and its calculation by removing the row and column of the current element. They proceed to demonstrate the computation for the second row of the matrix of minors, emphasizing the repetitive nature of the process.
🔄 Transition from Minors to Cofactors
The speaker transitions from the concept of minors to cofactors, explaining that the next step in matrix inversion is to convert the matrix of minors into a matrix of cofactors. They describe the pattern of alternating signs (plus, minus, plus) for the cofactors and apply this pattern to the matrix of minors to obtain the matrix of cofactors. The speaker emphasizes the importance of this step and reassures the audience that the complex terminology will be clarified in future videos. They also mention that understanding the process is crucial, even if the underlying principles may seem abstract at this stage.
🎓 Determinant and Inverse Calculation
The speaker concludes the matrix inversion process by calculating the determinant of matrix A using the matrix of cofactors. They explain that the determinant is the sum of the products of each element in the main diagonal with its corresponding cofactor. The speaker then calculates the determinant to be -1. They proceed to find the adjugate (or adjoint) of matrix A by transposing the matrix of cofactors, which involves swapping rows and columns. Finally, the speaker outlines the formula for finding the inverse of a matrix, which is 1/determinant times the adjugate of the matrix. They provide the calculated inverse matrix and suggest that the audience verify the result by multiplying it with the original matrix to obtain the identity matrix.
Mindmap
Keywords
💡Matrix inversion
💡Matrix of minors
💡Matrix of cofactors
💡Adjugate (Adjoint) matrix
💡Determinant
💡Identity matrix
💡Linear algebra
💡Computation
💡Algebra 2
💡Careless mistakes
Highlights
The speaker embarks on inverting a 3x3 matrix, which they find tedious but acknowledges its educational value.
Inverting larger matrices, such as 4x4, is even less pleasant and better suited for computers.
The process begins by creating a matrix of minors, which involves calculating determinants of submatrices.
The concept of minors is introduced as determinants resulting from removing a row and a column of the original matrix.
The calculation of the determinant of 2x2 submatrices is demonstrated with clear examples.
The transition from a matrix of minors to a matrix of cofactors is explained with a simple pattern of alternating signs.
The matrix of cofactors is visualized as a checkerboard pattern, aiding in understanding the conversion process.
The adjugate of a matrix is defined as the transpose of the matrix of cofactors.
The process of transposing involves flipping elements across the diagonal while keeping the diagonal elements the same.
The adjugate matrix is shown to be symmetric in this particular example.
The determinant of the original matrix is calculated using the matrix of cofactors.
The method for calculating the determinant is demonstrated with a step-by-step explanation.
The inverse of the matrix is found by multiplying the adjugate matrix by the reciprocal of the determinant.
The final calculated inverse matrix is presented, completing the demonstration.
The speaker suggests verifying the matrix inversion by multiplying the original and inverse matrices to obtain the identity matrix.
The process is described as taxing but emphasizes the importance of understanding the method for educational purposes.
Transcripts
Browse More Related Video

Inverting 3x3 part 1: Calculating matrix of minors and cofactor matrix | Precalculus | Khan Academy

Inverse of 3x3 matrix

Inverse of a 3x3 Matrix | Co-factor Method

Inverse Matrices and Their Properties

Inverse of a 3x3 Matrix - (THE SIMPLE WAY)
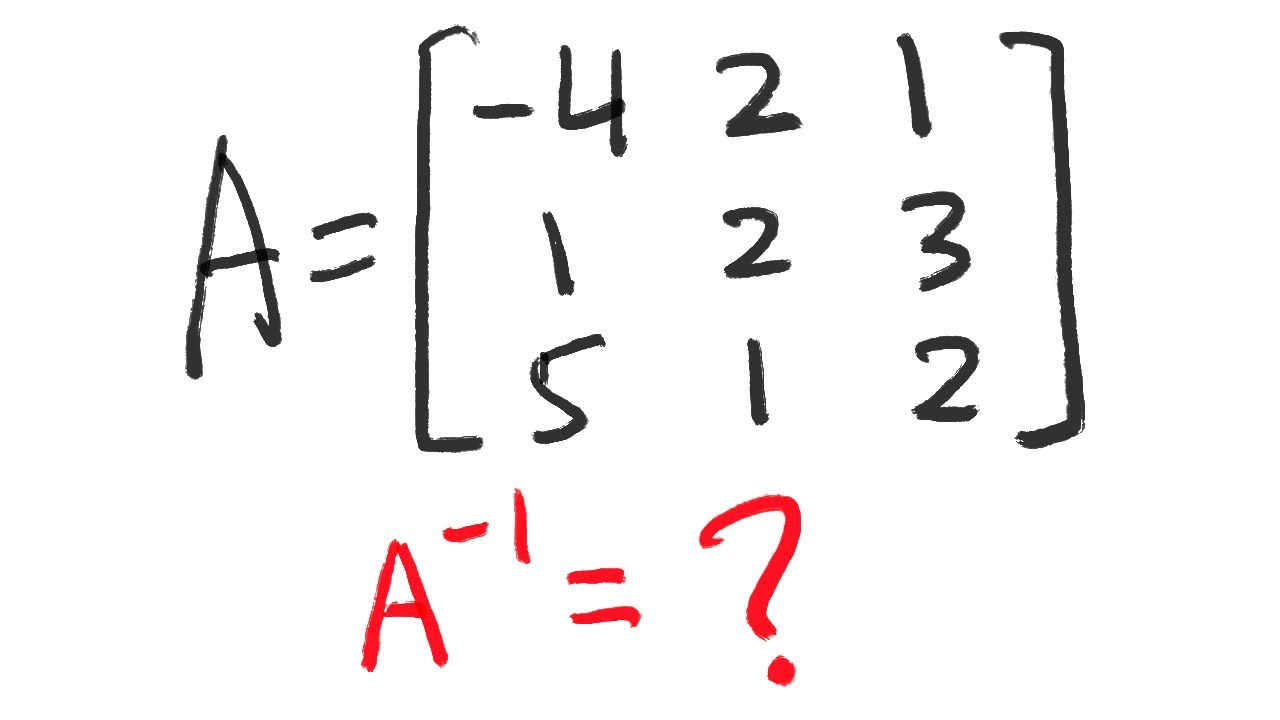
How to find the inverse of a 3 by 3 matrix (3 methods you need to know)
5.0 / 5 (0 votes)
Thanks for rating: