Solving for C on Separation of Variables Problems
TLDRThis video tutorial delves into the process of handling the constant 'plus c' that emerges when solving separable differential equations. The presenter addresses two common challenges: deciding where to place 'plus c' and determining the optimal time to solve for 'c'. The video simplifies the process by illustrating that 'plus c' should be placed alongside the independent variable, and emphasizes that solving for 'c' can be done at any point, though there are strategic moments that can simplify the process. The presenter works through several examples, demonstrating how to separate variables, integrate, and apply initial conditions to find the constant 'c'. The importance of considering the continuity of the function and ensuring that the initial condition falls within the solution's domain is highlighted. The tutorial concludes with practical advice on solving for 'c' after exponentiation when necessary, and the need to verify that the solution is both continuous and encompasses the initial condition.
Takeaways
- 📌 When solving separable differential equations, place the constant 'c' on the side with the independent variable.
- 🔍 The decision on when to solve for 'c' can be tricky and depends on the specific problem; it can be done at any point, but certain times may simplify the process.
- 🌟 For the first example, the differential equation d y d x = x * sqrt(y) with initial condition y(2) = 4 is solved by separating variables and integrating.
- 📐 After integrating, it's crucial to identify the independent variable to determine the correct side to place 'c'.
- 🧮 Solving for 'c' involves substituting known values of x and y into the integrated equation and solving the resulting equation.
- ✅ For continuous functions, there are no issues with the solution, but it's important to ensure the initial condition is satisfied.
- 📝 In the second example, the equation dy/dx = (x + 1)(y - 2) is tackled by separating variables and considering the properties of exponents.
- 🔑 Exponentiating before solving for 'c' can simplify the process, especially when dealing with natural logarithms.
- 📉 Absolute values in the equation can be handled by considering y - 2 as plus or minus the exponentiated term, which can be simplified by introducing new constants.
- 🔄 When applying initial conditions, ensure that the chosen constant 'c' aligns with the given y value at the specified x.
- 🧵 It's essential to check that the solution is continuous on the domain that includes the initial condition.
- ⚠️ Be cautious of the domain of the solution, especially when dealing with square roots and negative values, to ensure the initial condition is valid.
Q & A
What are the two main issues people encounter when solving separable differential equations?
-The two main issues are deciding where to place the 'plus c' term and when to solve for the constant 'c'. The first issue is resolved by placing 'plus c' on the side with the independent variable, and the second issue is more nuanced, with the solution depending on the specific problem and when it's most convenient to solve for 'c'.
How do you separate the variables in the given first example, dy/dx = x * sqrt(y)?
-To separate the variables, you would cross-multiply to get dy/sqrt(y) = x dx. Then, integrate both sides to isolate y.
What is the initial condition given for the first example, and how is it used to solve for the constant 'c'?
-The initial condition is y(2) = 4. It is used to solve for 'c' by substituting x = 2 and y = 4 into the integrated equation, allowing you to solve for the value of 'c'.
When is it most convenient to solve for the constant 'c'?
-It is most convenient to solve for 'c' after you have exponentiated if you need to exponentiate to solve for y, and it can be done at any point as long as no mistakes have been made up until that point.
What is the process for solving the second example, dy/dx = (x + 1)(y - 2)?
-First, separate the variables by integrating both sides. Then, use properties of exponents to rewrite the equation, and handle the absolute value by considering y - 2 as plus or minus the exponentiated term. Finally, apply the initial condition to solve for the constant 'c'.
How do you handle the absolute value in the second example?
-You handle the absolute value by considering y - 2 as plus or minus the exponentiated term, effectively turning it into a new constant that you can solve for using the initial condition.
What is the initial condition given for the third example, and how is it used?
-The initial condition is y(2) = -1. It is used to substitute into the integrated equation to solve for the constant 'c', and to ensure that the solution is valid for the given condition.
Why is it necessary to check the initial condition is in the range of your solution?
-Checking the initial condition is necessary to ensure that the solution is valid for the given problem. If the initial condition is not within the range of the solution, it means the solution does not satisfy the problem's requirements.
What is the importance of ensuring the function is continuous on the domain containing the initial condition?
-Ensuring the function is continuous on the domain containing the initial condition is crucial because the solution to a differential equation should be a continuous function that includes the initial condition to be valid.
Why is it recommended to exponentiate before solving for 'c' when dealing with logarithms?
-Exponentiating before solving for 'c' simplifies the process by eliminating the need to deal with logarithms, which can make solving for 'c' more straightforward and less prone to errors.
What is a common mistake to avoid when integrating with radicals?
-A common mistake to avoid is forgetting to include the integral sign when integrating. It's also helpful to convert radicals into rational exponents, especially if they appear in the denominator, by using negative exponents.
How can you determine which side to place the 'plus c' on when integrating?
-You determine the side to place 'plus c' on by looking at the original differential equation and identifying the independent variable. The 'plus c' is then placed on the side with the independent variable.
Outlines
📚 Introduction to Handling Plus C in Separable Differential Equations
This paragraph introduces the topic of dealing with the constant 'plus C' that arises when solving separable differential equations. It outlines two common issues: the placement of 'plus C' and when to solve for the constant 'C'. The paragraph emphasizes that 'plus C' is typically placed alongside the independent variable, and the decision on when to solve for 'C' depends on convenience and the specific problem at hand. The video provides examples to illustrate these concepts.
🔍 Solving the First Example: Separating Variables and Integrating
The first example involves a differential equation of the form d y/d x = x times the square root of y, with an initial condition y(2) = 4. The process begins with separating the variables and integrating both sides. The integral of y to the power of -1/2 dy is set equal to the integral of x dx. After integrating, the constant 'plus C' is placed on the side with the independent variable, which is x in this case. The constant 'C' is then solved for using the initial condition, resulting in a specific function for y in terms of x.
🧮 Solving the Second Example: Exponentiation and Absolute Values
The second example features a differential equation involving the product of (x + 1) and (y - 2). The solution process includes separating variables, integrating, and dealing with an absolute value by considering y - 2 as plus or minus the exponentiated expression. The constant 'C' is introduced during integration and is later solved for using initial conditions. The paragraph also discusses the importance of exponentiating before solving for 'C' to simplify the process and the handling of absolute values to avoid complications.
🔢 Final Considerations and Tips for Solving Differential Equations
The final paragraph discusses the steps for solving differential equations, emphasizing the flexibility in choosing when to solve for the constant 'C'. It advises exponentiating before solving for 'C' if necessary and to review the steps carefully to avoid mistakes. The paragraph also highlights the importance of checking that the initial condition is within the range of the solution and ensuring the function is continuous on the domain containing the initial condition. The speaker summarizes key points and offers encouragement for tackling such problems.
Mindmap
Keywords
💡Separable Differential Equation
💡Plus C
💡Independent Variable
💡Integration
💡Rational Exponents
💡Initial Conditions
💡Continuous Function
💡Exponentiation
💡Absolute Value
💡Domain
💡Natural Logarithm
Highlights
The video discusses handling the constant 'plus c' that appears when solving separable differential equations.
Two common issues are addressed: where to place 'plus c' and when to solve for c.
For the first issue, 'plus c' is placed on the side with the independent variable.
The decision on when to solve for c can be complex and depends on the situation.
Examples are used to illustrate the process of solving separable differential equations.
The first example involves the differential equation dy/dx = x * sqrt(y) with the condition y(2) = 4.
Integration techniques are demonstrated, including handling radicals and changing them into rational exponents.
The process of solving for c using initial conditions is shown, emphasizing the importance of accuracy.
The second example features the differential equation dy/dx = (x + 1)(y - 2), with y(0) = 5 as the initial condition.
The video explains the importance of exponentiating before solving for c when dealing with logarithmic expressions.
Handling absolute values and transforming them into plus or minus expressions is covered.
The concept of treating constants that result from operations as new constants is introduced.
A third example with the differential equation dy/dx = y^3/(x + 2)^2 and y(2) = -1 is solved, highlighting domain considerations.
The video emphasizes checking that the initial condition is within the range of the solution.
The importance of ensuring the function is continuous on the domain containing the initial condition is discussed.
The video concludes with a summary of key considerations when solving for c and handling differential equations.
The presenter advises reviewing the steps for solving for c, especially when exponentiation is involved.
Final advice includes ensuring the initial condition works and the solution is continuous with the given domain.
Transcripts
Browse More Related Video

Initial Value Problems!

Solving Basic Differential Equations with Integration (Differential Equations 6)

Introduction to Initial Value Problems (Differential Equations 4)

Modeling population with simple differential equation | Khan Academy
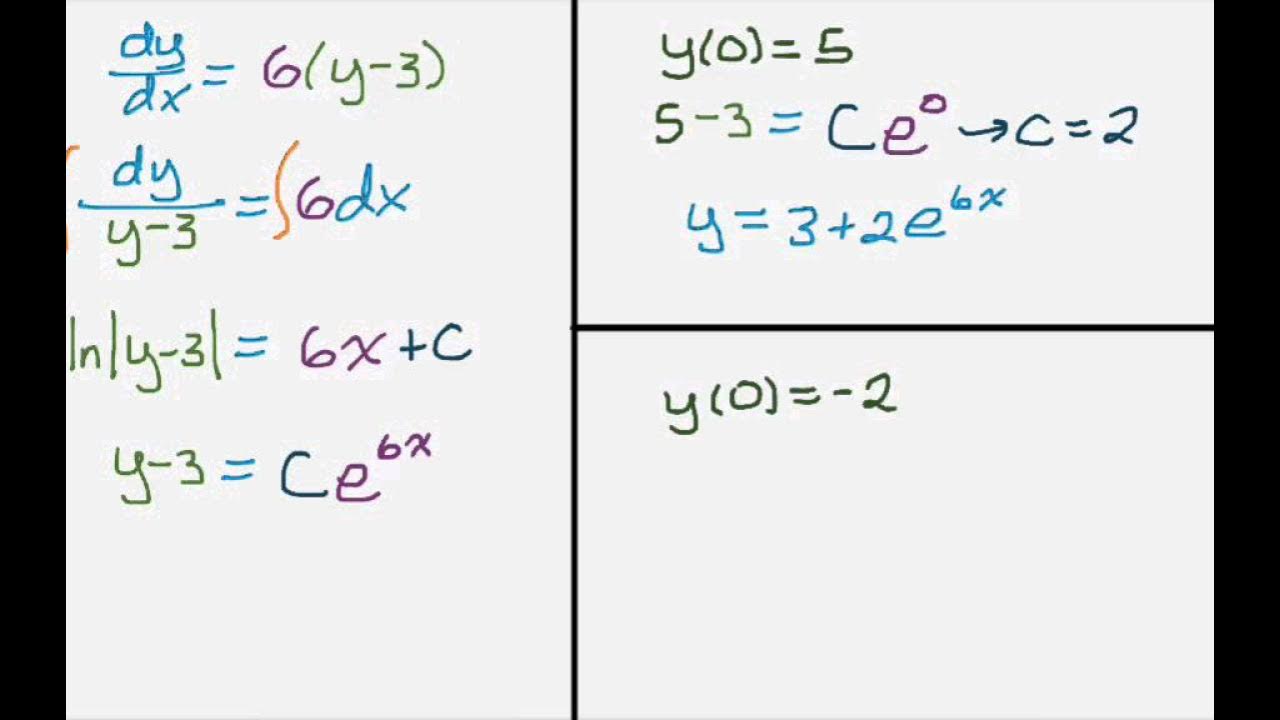
Separable Differential Equation (Natural Logs)

2022 AP Calculus AB Free Response #5
5.0 / 5 (0 votes)
Thanks for rating: