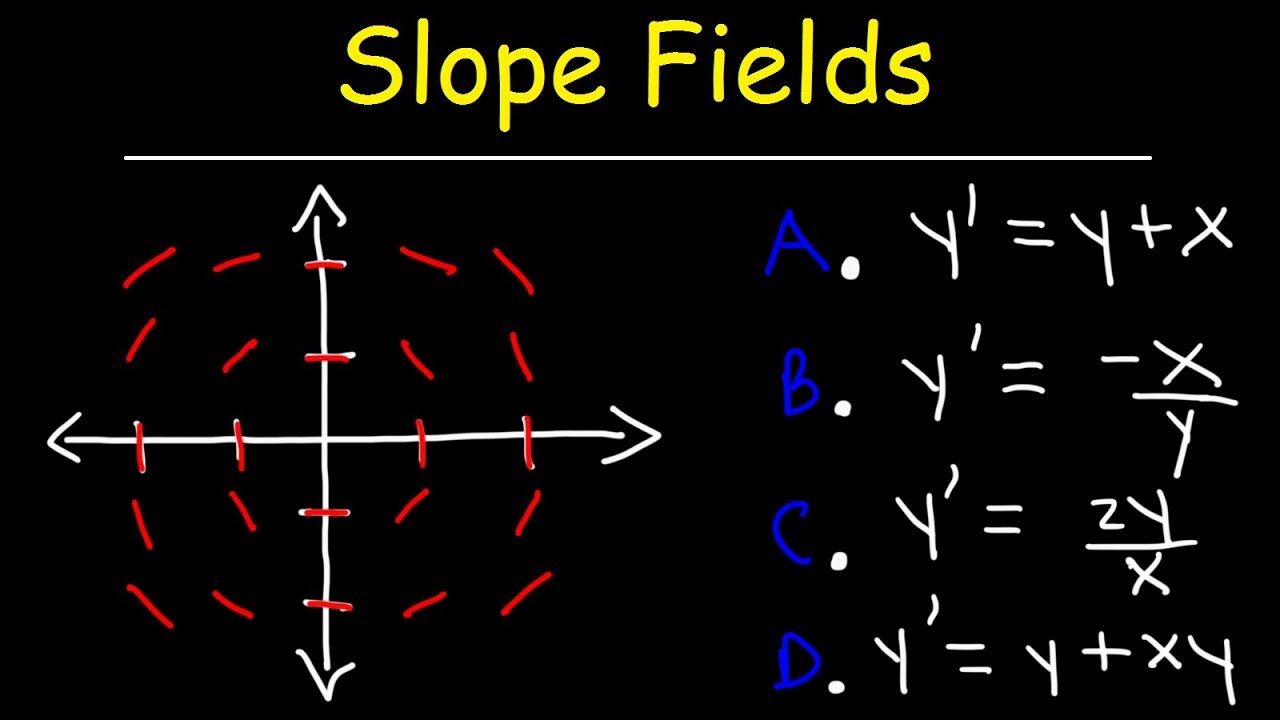
Matching Slope Fields to Differential Equations Part 2
TLDRThe video script discusses the process of matching slope fields to differential equations. The speaker outlines various strategies for identifying the correct differential equation based on the characteristics of the slope field. These strategies include looking for lines where the slope is zero, focusing on quadrants where the slope has a consistent sign, and testing specific points to determine the slope. The speaker also emphasizes the importance of considering whether the differential equation involves x, y, or both variables based on how the slope changes with respect to x and y. Additionally, sketching a solution curve and taking its derivative is mentioned as a useful technique. The summary provides a clear and concise overview of the methods used to match slope fields to their corresponding differential equations, offering viewers a helpful guide to understanding this mathematical concept.
Takeaways
- 📐 **Identify Slope Fields**: Look for places where the slope is zero to identify potential y-intercepts or asymptotes.
- 🔍 **Analyze Differential Equations**: Determine if the differential equation involves x, y, or both by observing changes in the slope field along horizontal and vertical lines.
- 📈 **Use Quadrants**: Focus on the behavior of slopes in different quadrants to narrow down the possible differential equations.
- 🎯 **Test Points**: Select a point and calculate the slope at that point to test which differential equation fits the slope field.
- 🔧 **Sketch Solution Curves**: Sometimes sketching a solution curve and taking its derivative can help identify the correct differential equation.
- 🧮 **Elimination Process**: Cross out options that do not match the observed behavior in the slope field.
- 📉 **Look for Extremes**: Identify lines of maximum or minimum slopes which can indicate where dy/dx equals zero.
- 📍 **Symmetry Axes**: Recognize lines of symmetry in the slope field which can correspond to constant values in the differential equation.
- 🔬 **Trigonometric Functions**: When the slope field resembles a trigonometric function, consider the derivatives of sine or cosine.
- 📊 **Zero-Slope Intersections**: Sketch lines where the slope is zero and match them to the differential equations that yield zero when set equal to the line's equation.
- ✅ **Confirm with Calculations**: Plug in specific values to confirm the differential equation, especially when the choice is not immediately clear.
Q & A
What is the main topic of the video?
-The video is about matching slope fields to differential equations.
What technique does the speaker use to identify the differential equation for number four?
-The speaker identifies two places where the slopes go to zero, which are y equals 0 and y equals 2, and then matches these with the given options.
How does the speaker determine the line x equals negative 1 in the slope field?
-The speaker observes that along this vertical line, dy/dx is always 0, indicating a minimum for all solution curves along that line.
Why does the speaker choose to focus on quadrant one for the next differential equation?
-The speaker notes that in quadrant one, where both x and y are greater than 0, dy/dx should be less than zero, allowing for the elimination of certain options.
What method does the speaker use to narrow down the options for the complicated-looking differential equation?
-The speaker uses a point, such as (1,1), to draw a tangent and observe the slope, which helps in choosing the correct differential equation based on the observed slope value.
How does the speaker approach the situation where there are two places with slopes going to zero?
-The speaker sketches in the lines where the slopes are zero, which are y equals 1 and y equals -1, and then selects the differential equation that matches this condition.
What does the speaker suggest for identifying trigonometric function situations in slope fields?
-The speaker suggests sketching a solution curve and observing the shape, which can resemble known trigonometric functions like cosine or sine.
What is the speaker's strategy for choosing a particular point to find the slope?
-The speaker selects a point, such as (1,1), and calculates the expected slope based on the differential equation, using this to confirm the correct equation.
How does the speaker determine the line y equals x minus 2?
-The speaker sketches a line that seems to represent a maximum along a certain line and identifies it as y equals x minus 2, which when substituted into the remaining options, confirms the correct differential equation.
What does the speaker suggest as a good starting point for identifying the differential equation?
-The speaker suggests focusing on where the slope is zero, as this can help eliminate many options and narrow down the selection.
How does the speaker approach the final slope field where there's only one option left?
-The speaker observes the shape of the slope field and notes that it resembles a positive cosine function, leading to the selection of the remaining differential equation.
What general tips does the speaker provide for matching differential equations to slope fields?
-The speaker recommends looking for lines where the slope is zero, focusing on quadrants to determine the sign of the slope, testing a point, and sketching a solution curve when possible.
Outlines
🔍 Identifying Differential Equations from Slope Fields
The speaker begins by introducing the task of matching slope fields to differential equations. They discuss the process of identifying where the slope of the field equals zero, which simplifies the matching process. The speaker uses the example of sketching y=0 and y=2 as places where the slope is zero. They then proceed to match these observations with the given options, narrowing down to the correct differential equation by process of elimination and logical deduction. The method involves looking at the behavior of the slope field and making educated guesses about the form of the differential equation that would produce such behavior.
📐 Techniques for Analyzing Slope Fields
The second paragraph delves into various techniques for analyzing slope fields. The speaker emphasizes the importance of looking at horizontal and vertical lines to determine whether x, y, or both are involved in the differential equation. They discuss the significance of quadrant analysis in identifying the nature of slopes within different regions of the graph. The speaker also mentions the use of test points and sketching solution curves as methods to match the slope field to the correct differential equation. They provide a summary of strategies, including focusing on where the slope is zero, which is a useful technique for solving these types of problems.
Mindmap
Keywords
💡Slope Field
💡Differential Equation
💡dy/dx
💡Solution Curve
💡Quadrant
💡Trigonometric Function
💡Zero Slope
💡Substitution
💡Extremum
💡Tangent Segment
💡Symmetry Axis
Highlights
The video discusses matching slope fields to differential equations, with a focus on identifying key characteristics of the slope field to determine the corresponding differential equation.
For the fourth slope field, the presenter identifies two horizontal lines (y=0 and y=2) where the slope is zero, which helps in narrowing down the differential equation.
The presenter uses a technique of substituting y values into potential differential equations to see which yields a zero dy/dx, successfully identifying the fourth equation.
The fifth slope field is characterized by a vertical line (x=-1) where the slope is zero, indicating a specific differential equation where dy/dx equals zero at this line.
In the sixth slope field, both x and y appear to influence the slope, as slopes change with both x and y, leading to a differential equation involving both variables.
The presenter suggests focusing on a quadrant where the slope characteristics are consistent, such as negative slopes in Quadrant 1, to eliminate options.
Choosing a specific point, like (1,1), and analyzing the slope at that point can help decide between remaining differential equation options.
The seventh slope field is quickly identified by the presenter as having two lines where the slope is zero, which directly leads to the corresponding differential equation.
Trigonometric functions are suspected in the eighth slope field, and the presenter sketches a solution curve resembling y = -cos(x), leading to the selection of the correct differential equation.
For the ninth slope field, the presenter uses a previous problem-solving experience to pick a particular point and find the slope, leading to the identification of the differential equation.
The tenth slope field is tackled by looking for a line where the slope is zero, which the presenter identifies as y = x - 2, and confirms by substituting into the remaining options.
The eleventh slope field is recognized by the presenter as having an axis of symmetry at x=2, where the slope is zero, leading to the selection of the corresponding differential equation.
In the twelfth slope field, the line y=x is identified as having a slope of 1, which helps the presenter to choose between the remaining differential equations.
The thirteenth slope field is solved by focusing on where the slope is zero, which the presenter sketches as y=2x, leading to the correct differential equation.
For the fourteenth slope field, the presenter eliminates options based on the observation that y=-2 is where the slopes are zero, leaving only one choice.
The fifteenth slope field is differentiated by the presenter as not being a trigonometric function, and a point like (1,1) is suggested for further distinction.
The sixteenth slope field is identified by the presenter as resembling a positive cosine function, which directly leads to the selection of the corresponding differential equation.
The presenter summarizes various techniques used throughout the video, such as focusing on lines with zero slopes, quadrant analysis, and testing points for slope characteristics.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: